2013/7/17 HNU_训练赛5
sgu 542 Gena vs Petya
sgu 543 Cafe
题意：有N组人需要被分配到某些固定了人数的桌子上，其中ai表示第i组有多少个人，安排作为需要符合如下安排：某一组的人员不能够单独在一张桌子，每张桌子坐的人数不能够超过其限制，问至少要安排多少张给定了人数限制的桌子。
分析：此题是一个贪心题，如果直接求解的话，由于桌子的数量是未知的，因此不太好分配，因此二分桌子的数量，在已知桌子的数量后运用贪心规则来求得最优解。但尽管在二分已知桌子的情况下还是不太好实现这个贪心规则。其思路是这样的：
1.如果桌子的限制为奇数，那么想办法把这些的桌子用奇数人数的组分出1个3来填，使得其限制变成偶数，这样是为了更好的填满奇数限制的桌子；
2.如果没有奇数人数的组，那么找出总人数大于等于6的组，分出尽可能多的6出来，把这个6分成2个3来填奇数限制的桌子，总而言之就是尽可能使得奇数限制的桌子能够被奇数的人数恰好填满；
3.处理完桌子后，就是统计各组人数的情况，如果还有奇数组，那么拿出一个3作为3人组，其余均变为2人组，最后统计一共有多少个3人组多少个2人组，这样做之后就使得不同组能够统一处理；
4.最后就是把这些3人组以及2人组分配到修正后的桌子上，先成对成对的放置3人组，这样能够使得尽可能的按照偶数分配，因为如果存在三人组，那么修正的桌子中一定不存在奇数限制的桌子（否则肯定会被奇数组的人填），不能成对分配之后再单个单个的分配，最后再分配2人组，如果都能够放下则说明二分的这个解成立，否则不成立。
#include <cstdlib> #include <cstdio> #include <cstring> #include <algorithm> #include <iostream> #include <vector> using namespace std; const int N = 2005; int n, r; int a[N], b[N]; struct E { int vol, num; E(int x, int y): vol(x), num(y) {} }; vector<E>v; bool Ac(int M) { // 判定M张桌子能否完成安排 int x, y; // x表示容量为偶数的桌子数量，y表示容量为奇数的桌子数量 if (r & 1) x = 0, y = M; else x = M, y = 0; memcpy(b, a, sizeof (a)); v.clear(); // 以下用来使得桌子尽可能多的转化为容量为偶数的桌子 if (r & 1) { for (int i = 0; i < n && y; ++i) { // 首先将奇数人中的3填到奇数容量的桌子中 if (b[i] & 1) { b[i] -= 3, y -= 1, x += 1; } } for (int i = 0; i < n && y >= 2; ++i) { // 只有当所有的奇数组人数都匹配后且奇数桌有剩余时才会执行此处 while (b[i] >= 6 && y >= 2) { b[i] -= 6, y -= 2, x += 2; } } // 如果还有奇数容量的桌子就一定没有奇数组的人或者是组员数大于6的偶数组 // 如果还有奇数个组员的组就一定没有奇数容量的桌子 if (x) v.push_back(E(r-3, x)); if (y) v.push_back(E(r, y)); } else { v.push_back(E(r, x)); } // 接下来求剩下各组人数的奇偶情况，p2、p3用来表示被分成2人组合3人组的组数 int p3 = 0, p2 = 0; for (int i = 0; i < n; ++i) { if (b[i] & 1) { b[i] -= 3, p3 += 1; } p2 += b[i] / 2; } // 先开始放置偶数对3人组，是因为这样不会使得桌子容量退化为奇数 for (int i = 0; i < v.size() && p3 >= 2; ++i) { if (v[i].vol >= 6) { int t1 = v[i].vol / 6; // 每个剩余的偶数桌子能够容纳多少对3 int t2 = min(v[i].num, p3/(2*t1)); // 已有的3人组能够占用多少张该桌子 if (t2 > 0) { p3 -= t2*t1*2; v[i].num -= t2; v.push_back(E(v[i].vol-6*t1, t2)); } if (v[i].num > 0 && p3 >= 2) { t2 = min(t1, p3/2); if (t2 > 0) { p3 -= t2*2; v[i].num -= 1; v.push_back(E(v[i].vol-6*t2, 1)); } } } } // 能够减掉偶数对3人组已经排除，因此只剩下一次减掉一次三人组的情况 for (int i = 0; i < v.size() && p3 > 0; ++i) { if(v[i].vol >=3 && v[i].num > 0) { int tmp = min(v[i].num, p3); p3 -= tmp; v[i].num -= tmp; v.push_back(E(v[i].vol-3, tmp)); } } if (p3 <= 0) { for (int i = 0; i < (int)v.size() && p2 > 0; ++i) { p2 -= (v[i].vol/2)*v[i].num; } } return p3 <= 0 && p2 <= 0; } int main() { while (scanf("%d %d", &n, &r) != EOF) { int ret; for (int i = 0; i < n; ++i) { scanf("%d", &a[i]); } int l = 1, r = n * 2000; while (l <= r) { int mid = (l + r) >> 1; if (Ac(mid)) { ret = mid; r = mid - 1; } else { l = mid + 1; } } printf("%d\n", ret); } return 0; }
sgu 544 Chess Championship
题意：类似于田忌赛马的一道题目，A、B双方分别有N位选手，每位选手的能力值被表示成不同的整数，2N位选手的能力值均不相同，现在问A赢B组K场的情况有多少种，也即能够安排出多少种一一对决的方式使得A组选手正好赢B组选手K次。
分析：设A组赢的次数为x，B组赢的次数为y，则由已知条件得x+y = N, x-y = K. 可以解出x和y值，如果不存在合理的解，那么输出0。原本自己想的是开设dp[i][j]表示A上场能力值第i大选手时赢得场数为j的方案数，但是很快觉得这个状态无法进行转移，因为仅仅单方面考虑A组上场顺序无法使得前后状态顺利递推，例如前i位的方案数中不同的方案对于i+1位选手的选择均不同。那么如何解决该问题呢，加状态，把A、B的选手情况通过状态完全的表示出来，那么这里细细一算会发现空间复杂度提高到了500^3，有超内存的风险，幸好正确的状态方程可以使用滚动数组来实现，因此在省下一维的情况下，还是能够把这个状态转移完成的。
为了表示方便，暂时不采用滚动数组来表示状态，先把A、B两组选手一起进行排序，第一维的i表示的就是这个新的数组的下标。设dp[i][j][k]表示到第i位选手为止，A组选手赢了j场，B组选手赢了k场的方案数。那么有状态转移方程：
如果是第i位选手为A组选手：dp[i][j][k] = dp[i-1][j-1][k] * (sb[i]-(j-1+k)) + dp[i-1][j][k];
否则：dp[i][j][k] = dp[i][j][k-1] * (sa[i]-(j-1+k)) + dp[i-1][j][k]. 其中sa[i]、sb[i]表示前i位选手中分别有多少位A组、B组选手，sa[i]+sb[i] = i.
方程表示这个状态可以通过两个方式转移过来，第一种是第i位选手去赢前面还没有匹配的对手，因为已经排序的序列，因此未匹配的对手一定会输给当前选手；第二种选择是将当前选手变为未匹配的选手。这种状态的表示方式观察的是两组选手的前若干位选手的状态，而不是单单的A组或者是B组选手的状态，因此得到了正确的答案。在处理的时候还要注意某些不合法的状态不能够进行计算。例如当前若是A组选手，那么赢得的场数应该是min(sa[i], sb[i])，反正就是在剩下的选手中发生匹配的对数，其余的只有剩下来。
#include <cstdlib> #include <cstring> #include <cstdio> #include <algorithm> #include <iostream> using namespace std; const int N = 505; const int mod = int(1e9)+9; int n, k; int sa[N<<1], sb[N<<1]; int f[2][N][N]; struct Node { int who, val; bool operator < (const Node &other) const { return val < other.val; } }e[N<<1]; void gao() { int LIM = n << 1; int fa = (n+k)%2 ? -1 : (n+k)/2; int fb = (n-k)%2 ? -1 : (n-k)/2; if (n < k || !(~fa) || !(~fb)) { puts("0"); return; } for (int i = 1; i <= LIM; ++i) { if (!e[i].who) { sa[i] = sa[i-1] + 1; sb[i] = sb[i-1]; } else { sa[i] = sa[i-1]; sb[i] = sb[i-1] + 1; } } int cur = 0; f[!cur][0][0] = 1; for (int i = 1; i <= LIM; ++i) { int la = min(sa[i], sb[i]); for (int j = 0; j <= la; ++j) { int lb = min(sb[i]-j, sa[i]-j); for (int k = 0; k <= lb; ++k) { if (!e[i].who) { // 如果是a的选手 if (j > 0) f[cur][j][k] = (1LL*f[cur][j][k] + 1LL*f[!cur][j-1][k] * (sb[i] - (j-1+k))) % mod; f[cur][j][k] = (1LL*f[cur][j][k] + f[!cur][j][k]) % mod; } else { // 如果是b的选手 if (k > 0) f[cur][j][k] = (1LL*f[cur][j][k] + 1LL*f[!cur][j][k-1] * (sa[i] - (j-1+k))) % mod; f[cur][j][k] = (1LL*f[cur][j][k] + f[!cur][j][k]) % mod; } // printf("f[%d][%d][%d] = %d\n", i, j, k, f[cur][j][k]); // getchar(); } } cur = !cur; memset(f[cur], 0, sizeof (f[cur])); } // printf("fa = %d, fb = %d\n", fa, fb); printf("%d\n", f[!cur][fa][fb]); } int main() { while (scanf("%d %d", &n, &k) != EOF) { memset(f, 0, sizeof (f)); memset(sa, 0, sizeof (sa)); memset(sb, 0, sizeof (sb)); for (int i = 1; i <= n; ++i) { e[i].who = 0; scanf("%d", &e[i].val); } for (int i = 1; i <= n; ++i) { e[n+i].who = 1; scanf("%d", &e[n+i].val); } sort(e+1, e+(n<<1)+1); gao(); } return 0; }
sgu 545 Cut the rope, another rope and so on!
sgu 546 Ternary Password
题意：给定长度为N的一个只有0、1、2组成的密码，现在要求将密码变成一个0的数量为a，1的数量为b的密码串要需要多少次操作，题中只定义了一种操作，即替换操作：能够将原串中的某一位变成另一位数字。最后输出修改后的密码串。
分析：dp[i][j][j]表示前i为包含j个0,k个1所需要的最少的替换次数为多少。使用dfs输出最后结果，相当于重新做了一个动态规划。因此有动态规划方程：
当i位置为0时，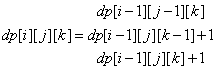
，其余位置类似。 事后，被告知该题就是简单的模拟题，直接统计下0、1、2的个数即可，囧了。
#include <cstdlib> #include <cstring> #include <cstdio> #include <iostream> #include <algorithm> using namespace std; int f[205][205][205]; int N, a, b; char str[205]; void dfs(int i, int j, int k) { if (i == 0) return; if (str[i] == '0') { if (j - 1 >= 0 && f[i][j][k] == f[i-1][j-1][k]) dfs(i-1, j-1, k); else if (k - 1 >= 0 && f[i][j][k] == f[i-1][j][k-1] + 1) str[i] = '1', dfs(i-1, j, k-1); else if (f[i][j][k] == f[i-1][j][k] + 1) str[i] = '2', dfs(i-1, j, k); } else if (str[i] == '1') { if (j - 1 >= 0 && f[i][j][k] == f[i-1][j-1][k] + 1) str[i] = '0', dfs(i-1, j-1, k); else if (k - 1 >= 0 && f[i][j][k] == f[i-1][j][k-1]) dfs(i-1, j, k-1); else if (f[i][j][k] == f[i-1][j][k] + 1) str[i] = '2', dfs(i-1, j, k); } else { if (j - 1 >= 0 && f[i][j][k] == f[i-1][j-1][k] + 1) str[i] = '0', dfs(i-1, j-1, k); else if (k - 1 >= 0 && f[i][j][k] == f[i-1][j][k-1] + 1) str[i] = '1', dfs(i-1, j, k-1); else if (f[i][j][k] == f[i-1][j][k]) dfs(i-1, j, k); } } void gao() { memset(f, 0x3f, sizeof (f)); f[0][0][0] = 0; for (int i = 1; i <= N; ++i) { for (int j = 0; j <= i; ++j) { for (int k = 0; k <= i-j; ++k) { int Min = 100000; if (str[i] == '0') { if (j - 1 >= 0) Min = min(Min, f[i-1][j-1][k]); if (k - 1 >= 0) Min = min(Min, f[i-1][j][k-1] + 1); Min = min(Min, f[i-1][j][k] + 1); } else if (str[i] == '1') { if (j - 1 >= 0) Min = min(Min, f[i-1][j-1][k] + 1); if (k - 1 >= 0) Min = min(Min, f[i-1][j][k-1]); Min = min(Min, f[i-1][j][k] + 1); } else { if (j - 1 >= 0) Min = min(Min, f[i-1][j-1][k] + 1); if (k - 1 >= 0) Min = min(Min, f[i-1][j][k-1] + 1); Min = min(Min, f[i-1][j][k]); } f[i][j][k] = Min; } } } printf("%d\n", f[N][a][b]); dfs(N, a, b); for (int i = 1; i <= N; ++i) { printf("%c", str[i]); } puts(""); } int main() { while (scanf("%d %d %d", &N, &a, &b) != EOF) { scanf("%s", str+1); if (strlen(str+1) != N || a + b > N) { puts("-1"); continue; } gao(); } return 0; }
sgu 547 Divide the Kingdom
sgu 548 Dragons and Princesses
题意：给定N个格子，编号为1-N，骑士现在在1号格子，2-N号格子中有恶龙或者是公主，如果是恶龙的话，那么战胜每条恶龙能够得到一定的金币，如果是公主，那么之前斩杀的恶龙数量如果大于或者等于该公主的要求，则这个公主就嫁给骑士。骑士之喜欢位于编号为N格子中的公主，因此骑士必须不满足前面任何一个公主的要求，并且使得最后所赢得的金币最多。
分析：从前往后，选择一个优先队列，每次遇到恶龙，加入到队列中，如果遇到公主，则把金币小的恶龙全部退出来，然后再接着斩杀恶龙，最后一个公主不需要处理，如果最后斩杀的恶龙不足以满足最后一个公主的要求，输出-1。
#include <cstdlib> #include <cstring> #include <iostream> #include <cstdio> #include <algorithm> #include <queue> using namespace std; int N; struct Node { char str[5]; int val, No; bool operator < (const Node & other) const { return val > other.val; } }e[200005]; priority_queue<Node>q; vector<Node>v; bool cmp(const Node &a, const Node &b) { return a.No < b.No; } int main() { while (scanf("%d", &N) != EOF) { v.clear(); for (int i = 2; i <= N; ++i) { e[i].No = i; scanf("%s %d", e[i].str, &e[i].val); } for (int i = 2; i < N; ++i) { if (e[i].str[0] == 'p') { while (q.size() >= e[i].val) q.pop(); } else { q.push(e[i]); } } if (q.size() < e[N].val) { puts("-1"); continue; } int tot = 0; while (!q.empty()) { v.push_back(q.top()); tot += q.top().val; q.pop(); } sort(v.begin(), v.end(), cmp); printf("%d\n%d\n", tot, v.size()); for (int i = 0; i < (int)v.size(); ++i) { printf(i == 0 ? "%d" : " %d", v[i].No); } puts(""); } return 0; }
sgu 549 Dumbbells
题意：给定了若干个哑铃，现在要求将这些哑铃分组出售，每组哑铃必须要由k个不同质量的哑铃组成，优先哑铃组数最多，然后哑铃的价格之和最大。
分析：将相同质量的哑铃统计起来，并且使用vector把不同质量的哑铃所拥有的价格保存起来，最后通过不同质量的哑铃个数是否大于k个，如果不足输出-1，否则统计前k个数量最多的质量相同的哑铃中数量最少的一种作为能够组成的组数，然后将数量大于该组数的哑铃价值排在前k的统计出来，最后再取和值最大的前k个。
#include <cstdlib> #include <cstring> #include <cstdio> #include <algorithm> #include <iostream> #include <vector> using namespace std; int N, K; int w[4005], c[4005]; int cnt[4005], pos[4005]; int seq[4005]; int idx; vector<int>v[4005]; // 分别表示重量和价值 bool cmp(int a, int b) { return cnt[a] > cnt[b]; } bool cmp2(int a, int b) { return a > b; } void gao(int suit) { // 能够生产x套哑铃 int ret = 0, n = 0; for (int i = 1; i <= 4000; ++i) { if (cnt[pos[i]] >= suit) { int tmp = 0; sort(v[pos[i]].begin(), v[pos[i]].end(), cmp2); for (int j = 0; j < suit; ++j) tmp += v[pos[i]][j]; seq[n++] = tmp; } } sort(seq, seq+n, cmp2); for (int i = 0; i < K; ++i) { ret += seq[i]; } printf("%d %d\n", suit, ret); } int main() { while (scanf("%d %d", &N, &K) != EOF) { memset(cnt, 0, sizeof (cnt)); for (int i = 1; i <= 4000; ++i) { pos[i] = i; v[i].clear(); } for (int i = 0; i < N; ++i) { scanf("%d %d", &w[i], &c[i]); v[w[i]].push_back(c[i]); // 这个质量的哑铃后面有这么些价值的选择 ++cnt[w[i]]; } sort(pos+1, pos+4001, cmp); idx = 4000; for (int i = 1; i <= 4000; ++i) { if (cnt[pos[i]] == 0) { idx = i - 1; break; } } if (idx < K) { puts("0 0"); continue; } int suit = 100000; for (int i = 1; i <= K; ++i) { suit = min(suit, cnt[pos[i]]); } // suit表示能够得到的最多的套数 gao(suit); } return 0; }
sgu 550 Tree Queries Online
sgu 551 Preparing Problem
题意：现有N个工作，甲完成这件工作需要t1时间，乙完成这件工作需要t2时间，现在两人同时开始进行工作，问最后一共完成多少个工作。甲乙开工后不能够中断，没完成一个工作后马上检查是否已经有N个工作，如果没有的话继续下一次工作。
分析：由于数据范围较小，因此可以直接进行模拟，维护好两个时间值，分别表示甲和乙完成下一件工作的时间，如果两着完成下一次工作的时间相同的话，那么同时处理，如果不同的话，一个一个进行处理。
#include <cstdlib> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; int N, a, b; int main() { while (scanf("%d %d %d", &N, &a, &b) != EOF) { int ta = a, tb = b, finish = 0, sp; while (finish < N) { if (ta == tb) { finish += 2; if (finish < N) ta += a, tb += b; } else { sp = min(ta, tb); if (ta == sp) { ++finish; if (finish < N) ta += a; else ++finish; // b还有一件正在做 } else { ++finish; if (finish < N) tb += b; else ++finish; // a还有一件正在做 } } } printf("%d %d\n", finish, max(ta, tb)); } return 0; }
sgu 552 Database Optimization
题意：给定一些数据，告诉你每个数据有多少个关键字，然后给出这些关键字，现在要求给定一种算法使得多关键字查询的过程加快。
分析：由于给定的每条信息的关键字最多只有4条，因此我们可以直接将每条信息的关键字排序后使用二进制枚举出所有的组合情况，抽取出关键字使用map来存储，查询的时候采用同样的处理方式就可以了。注意：每条关键字之前插入一个分隔符防止因为相连导致的错误。
#include <cstdlib> #include <cstring> #include <cstdio> #include <string> #include <algorithm> #include <iostream> #include <map> using namespace std; map<string,int>mp; int N, M; string str[4]; int main() { while (cin >> N) { int x; mp.clear(); for (int i = 0; i < N; ++i) { cin >> x; for (int j = 0; j < x; ++j) { cin >> str[j]; } sort(str, str+x); int mask = 1 << x; for (int j = 0; j < mask; ++j) { string tmp; for (int k = 0; k < 4; ++k) { if (j & (1 << k)) { tmp += " " + str[k]; } } ++mp[tmp]; } } cin >> M; while (M--) { cin >> x; for (int i = 0; i < x; ++i) { cin >> str[i]; } sort(str, str+x); string tmp; for (int i = 0; i < x; ++i) { tmp += " " + str[i]; } printf("%d\n", mp[tmp]); } } return 0; }
sgu 553 Sultan's Pearls
题意：有N颗珍珠放置在桌子上，其中有M颗悬挂中空中，现在要求每次从首或者是尾拿掉一颗珍珠，每次从尾部拿掉一颗珍珠，那么就人为的使得珍珠向下滑动一格，使得悬空的珍珠的数量保持不变，现在给定每颗珍珠的价值以及质量，要求最多拿到多少价值的珍珠，并输出任意一种拿的方案。如果在拿的过程中出现了悬挂在空中的珍珠的总质量大于放置在桌子上的珍珠的总质量之和乘上一个给定的摩擦系数k，那么宣告该次操作不合法，要求在所有操作均合法的情况下，能够拿到的最多的价值的珍珠。
分析：此题刚看时以为是动态规划，但是无奈数据范围太大，无法开设两维的状态来容纳下所有的情况，因此需要找到题中的一些特殊的特性。经过观察可以发现，若最终的结果是拿走了悬空的x颗珍珠，那么这x颗珍珠一开始就连续的拿是一定能够拿走的，因为先拿桌子上的珍珠意味着上面的重量减少了。因此此题做法便是枚举能够拿走的悬空的珍珠的数量，然后再二分查找能够能够从桌子上面拿走的珍珠数量。
#include <cstdlib> #include <cstring> #include <cstdio> #include <iostream> #include <algorithm> using namespace std; int N, M, K; struct Node { int w, c; }e[200005]; int fsum[200005]; int tsum[200005]; int fpri[200005]; int tpri[200005]; bool judge(int x) { // 在未取下左面上的情况下，是否能够取下悬挂的x个珠子 if (x >= N-M) return false; int u = N-x-M+1, d = N-x; if (tsum[u] - tsum[d+1] > K*fsum[u-1]) return false; else return true; } bool legal(int y, int x) { int u = N-x-M+1, d = N-x; int l = y+1, r = u - 1; if (tsum[u] - tsum[d+1] > K*(fsum[r] - fsum[l-1])) return false; else return true; } void gao() { int ret = -1, x, y; // ret保存的是能够获得的最大价值，x表示取了多少颗悬空的，y表示桌子上取了多少颗 for (int i = 0; judge(i); ++i) { int l = 0, r = N-i-M-1; // 至少要留一颗珠子在桌子上 while (l <= r) { int mid = (l + r) >> 1; if (legal(mid, i)) { int tmp = fpri[mid] + tpri[N-i+1]; if (tmp > ret) { x = i, y = mid; ret = tmp; } l = mid + 1; } else { r = mid - 1; } } } printf("%d %d\n", x + y, ret); for (int i = 0; i < x; ++i) putchar('H'); for (int i = 0; i < y; ++i) putchar('T'); puts(""); } int main() { while (scanf("%d %d %d", &N, &M, &K) != EOF) { for (int i = 1; i <= N; ++i) { scanf("%d %d", &e[i].w, &e[i].c); } tsum[N+1] = tpri[N+1] = 0; for (int i = 1, j = N; i <= N; ++i, --j) { fsum[i] = fsum[i-1] + e[i].w; fpri[i] = fpri[i-1] + e[i].c; tsum[j] = tsum[j+1] + e[j].w; tpri[j] = tpri[j+1] + e[j].c; } gao(); } return 0; }