HDU 1710 Binary Tree Traversals (二叉树遍历)
Binary Tree Traversals
Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2442 Accepted Submission(s): 1063
Problem Description
A binary tree is a finite set of vertices that is either empty or consists of a root r and two disjoint binary trees called the left and right subtrees. There are three most important ways in which the vertices of a binary tree can be systematically traversed or ordered. They are preorder, inorder and postorder. Let T be a binary tree with root r and subtrees T1,T2.
In a preorder traversal of the vertices of T, we visit the root r followed by visiting the vertices of T1 in preorder, then the vertices of T2 in preorder.
In an inorder traversal of the vertices of T, we visit the vertices of T1 in inorder, then the root r, followed by the vertices of T2 in inorder.
In a postorder traversal of the vertices of T, we visit the vertices of T1 in postorder, then the vertices of T2 in postorder and finally we visit r.
Now you are given the preorder sequence and inorder sequence of a certain binary tree. Try to find out its postorder sequence.
In a preorder traversal of the vertices of T, we visit the root r followed by visiting the vertices of T1 in preorder, then the vertices of T2 in preorder.
In an inorder traversal of the vertices of T, we visit the vertices of T1 in inorder, then the root r, followed by the vertices of T2 in inorder.
In a postorder traversal of the vertices of T, we visit the vertices of T1 in postorder, then the vertices of T2 in postorder and finally we visit r.
Now you are given the preorder sequence and inorder sequence of a certain binary tree. Try to find out its postorder sequence.

Input
The input contains several test cases. The first line of each test case contains a single integer n (1<=n<=1000), the number of vertices of the binary tree. Followed by two lines, respectively indicating the preorder sequence and inorder sequence. You can assume they are always correspond to a exclusive binary tree.
Output
For each test case print a single line specifying the corresponding postorder sequence.
Sample Input
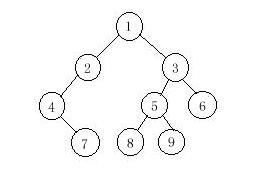
9 1 2 4 7 3 5 8 9 6 4 7 2 1 8 5 9 3 6
Sample Output
7 4 2 8 9 5 6 3 1
Source
Recommend
lcy
题意:
给你一个前序遍历和中序遍历,要求后序。
可以由先序和中序的性质得到 : 先序的第一个借点肯定是当前子树的根借点, 那么在
中序中找到这个结点, 则这个结点左边的节点属于左子树, 右边的属于右子树。然后递归遍历就可以了。
#include<iostream> #include<cstdio> #include<cstring> #include<stack> using namespace std; const int N=1010; int n,pre[N],in[N]; //先序数组和后序数组 stack<int> st; //存放父节点 void build(int l1,int r1,int l2,int r2){ //l1,r1,是先序遍历的数组的开始和末尾,l2,r2是中序遍历的数组的开始和末尾 int i,j; st.push(pre[l1]); //父节点入栈 for(i=l2;i<=r2;i++) if(in[i]==pre[l1]) //找到父节点在中序遍历的位置i break; j=l1+(i-l2+1); //确定左子树和右子树在先序遍历的分界点j,即右子树的父节点 if(j<=r1 && i+1<=r2) //求解右子树 build(j,r1,i+1,r2); if(l1+1<=j-1 && l2<=i-1) //求解左子树 build(l1+1,j-1,l2,i-1); } int main(){ //freopen("input.txt","r",stdin); while(~scanf("%d",&n)){ for(int i=0;i<n;i++) scanf("%d",&pre[i]); for(int i=0;i<n;i++) scanf("%d",&in[i]); build(0,n-1,0,n-1); while(!st.empty()){ printf("%d",st.top()); st.pop(); if(!st.empty()) printf(" "); } printf("\n"); } return 0; }
#include<iostream> #include<cstdio> #include<cstring> #include<stack> #include<cstdlib> using namespace std; const int N=1010; struct Tree{ Tree *l,*r; int x; }tree; Tree *root; Tree *Create(int *pre,int *in,int n){ Tree *tmp; for(int i=0;i<n;i++) if(pre[0]==in[i]){ //找到中序遍历时的根节点 tmp=(Tree *)malloc(sizeof(Tree)); tmp->x=in[i]; tmp->l=Create(pre+1,in,i); //中序历遍中在根节点左边的都是左子树上的 tmp->r=Create(pre+i+1,in+i+1,n-(i+1)); //在根节点右边的,都是右子树上的,右子树需要从i+1开 return tmp; } return NULL; } void PostOrder(Tree *rt){ //后序历遍 if(rt!=NULL){ PostOrder(rt->l); PostOrder(rt->r); if(rt==root) printf("%d\n",rt->x); else printf("%d ",rt->x); } } int main(){ //freopen("input.txt","r",stdin); int n,pre[N],in[N]; //先序数组和后序数组 while(~scanf("%d",&n)){ root=NULL; for(int i=0;i<n;i++) scanf("%d",&pre[i]); for(int i=0;i<n;i++) scanf("%d",&in[i]); root=Create(pre,in,n); Tree *rt=root; PostOrder(rt); } return 0; }