萌新做点小玩意儿DAY-3 运用递归和分治的棋盘覆盖算法

今天复习了一下很久很久前学过的分治和递归算法思想。

分治顾名思义分而治之，当面对一个规模比较大的问题时，暴力解决问题则会面临庞大的计算量，因此并不妥当，我们可以把一个大的问题转换为规模相同的子问题，通过调用解决子问题的算法来解决整个问题。

在我看来递归并不是一种算法而是解决问题的一种思想，最常见的递归计算就是计算n!和斐波那契数列，递归的特点就是代码实现起来比较快捷，短短的几行代码就可以计算解决斐波那契数列问题。而非递归的方式则要实现一个很复杂很复杂的函数。

int Fibonacci(int n){
  if(n <= 1)
    return 1;
  return Fibonacci(n-1)+Fibonacci(n-2);
}

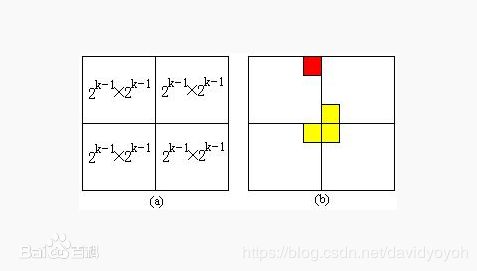
今天解决的问题就是棋盘覆盖问题。问题描述：在一个2^k*2^k的方格组成的一个棋盘上，恰有一个方格与其他方格不同，称之为特殊方格，显然特殊方格出现的概率有4^种情况，图例中的（a）是k=2中的一种情况，棋盘覆盖问题要求用（b）中的四种L型骨牌覆盖满给定棋盘上除特殊方格以外的所有方格，且要求任何两个骨牌不能重叠覆盖。

（本图源自百度百科）

运用分治策略时，可以将棋盘分为4个2^k-1*2^k-1个子棋盘，特殊方格一定在子棋盘其中之一，其余三个棋盘中无特殊方格，可以进一步在这三个子棋盘的汇合处添加一个L骨牌将这三个子棋盘转换为规模相同的有一个特殊方格的子棋盘，再进行递归的分割，直至棋盘为1*1为止。

（图片源自百度百科）

用C++实现代码如下

#include 
using namespace std;

const int max = 100;
int title = 1;
int Board[max][max];
int X,Y,SIZE;

//tx:Line number of the upper left corner of the checkerboard
//ty:Column number of the upper left corner of the checkerboard
//x:The line number of the special square
//y:The column number of the special square
//size:The size of the chessboard
void Chessboard(int tx, int ty, int x, int y, int size){
	if (size == 1)
		return;
	int t = title++;                       //The type of L
	int s = size/2;                            //Divide the board in half
    if (x < tx+s && y < ty+s)              //If the special square is in the upper left corner of the checkerboard
		Chessboard(tx,ty,x,y,s);           //Divide again
	else {
		Board[tx+s-1][ty+s-1] = t;         //Cover the lower right corner
        Chessboard(tx,ty,tx+s-1,ty+s-1,s); //Overlaying board
	}
	 if (x < tx+s && y >= ty+s)            //If the special square is in the top right corner of the checkerboard
		Chessboard(tx,ty+s,x,y,s);         
	else {
		Board[tx+s-1][ty+s] = t;         
        Chessboard(tx,ty+s,tx+s-1,ty+s,s);
	}
	 if (x >= tx+s && y < ty+s)             //If the special square is in the lower left corner of the checkerboard
		Chessboard(tx+s,ty,x,y,s);           
	else {
		Board[tx+s][ty+s-1] = t;         
        Chessboard(tx+s,ty,tx+s,ty+s-1,s);
	}
	 if (x >= tx+s && y >= ty+s)            //If the special square is in the lower left corner of the checkerboard
		Chessboard(tx+s,ty+s,x,y,s);         
	else {
		Board[tx+s][ty+s] = t;         
        Chessboard(tx+s,ty+s,tx+s,ty+s,s);
	}
}

int main(){
	cout <<"请输入特殊方格坐标和棋盘规格"<< endl;
	cin >>X>>Y>>SIZE;
	   Chessboard(0,0,X,Y,SIZE);
	   for(int i = 0; i < SIZE; i ++){
        for(int j = 0; j < SIZE; j ++){
            cout <

代码测试效果图：

整个算法的时间复杂度也是显而易见的，

T(K)=1 (K=0)

T(K)=4T(K-1)

可得T(K)=O(4^K)。

总而言之，棋盘覆盖算法属于比较简单而且比较经典的递归分治算法，比较适用于刚接触这种算法思想的人去写一写尝试一下。而递归分治更多的用在排序问题上，比如快排和合并排序，能够在一定程度上优化问题解决的时间复杂度。