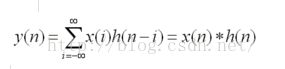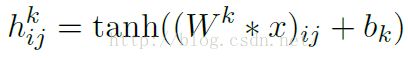深度学习之：CNN卷积神经网基本概念理解

1.整理下网上介绍CNN比较好的博客

    以下是本人觉得介绍CNN比较好的几篇博客，本文也是在这些大牛们的博客基础下，写一下自己对CNN的一些理解，自己水平有限，难免有理解错误的地方，欢迎有兴趣的朋友多多指正，共同进步。

[1]Deep Learning简介 

[2]深度学习笔记整理系列

[3]Deep Learning模型之：CNN卷积神经网（1）深度解析CNN

[3]卷积神经网介绍：网络框架、源码解析

[4]一文读懂CNN卷积神经网

2. 简单介绍下卷积操作

       要理解卷积神经网，首先要对二维图像的卷积操作有个大致概念,这里简单介绍下卷积：

     1）一维空间的卷积，这个学过信号与系统的同学应该都了解，以离散系统为例：

     

     其中星号*表示卷积，x(n)是一个线性时不变系统，h(n)是一个滤波器，由以上公式可以看出，离散系统一维卷积操作就是将两个离散序列 和 之间按照一定的规则将它们的有关序列值分别两两相乘再相加。

   2）二维图像卷积，理解二维图像卷积是理解卷积神经网的基础

     

         对二维图像卷积操作，其数学意义可以解释如下：

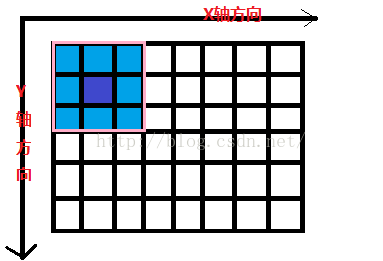
     源图像是作为输入源数据，处理以后要得到的图像是卷积输出结果，卷积操作函数作为Filter，在X、Y两个方向上对源图像的每个像素点实施卷积操作。如图所示：粉红色的方格表示一个滤波器，黑色方格表示输入图像，每个方格表示一个像素，粉红色方格覆盖输入图像的某个区域就表示对该区域做卷积。该粉红色方格每次在X、Y前进一个像素方格（即对该像素区域做卷积），就会产生一个新的输出像素，图中正中间深蓝色的代表要输出的像素方格，走完全部的像素方格，就得到了所有输出像素。

     利用卷积可以实现对图像模糊处理，边缘检测，产生轧花效果的图像。

     想对二维图像卷积操作有更详细了解的话，可以参考这篇博客。

3.CNN概述

     CNN全名叫卷积神经网（Convolutional Neural Networks），是一种特殊的深层的神经网络模型，在图像处理领域应用的比较广泛，并且取得了不错的效果。CNN相对于传统的图像处理方法的优势在于:传统的图像处理需要先通过一些算法提取图像的颜色特征、纹理特征、形状特征、空间关系特征，然后根据这些特征做图像分类或者图像检索等应用，而CNN直接将整个图像作为输入，CNN算法自动提取图像特征；而相对于全连接神经网，CNN的的神经元之间的连接是非全连接的，而且CNN的同一层中某些神经元之间的连接的权值是共享的，这种权值共享网络结构使之更类似于生物神经网络，降低了网络模型的复杂度，减少了权值的数量。

  如上所述，CNN相对于全连接网络的一个优势是局部连接和权值共享，CNN通过局部连接和权值共享可以有效减少模型参数，下面用一个网上常见的图说明该问题：

  

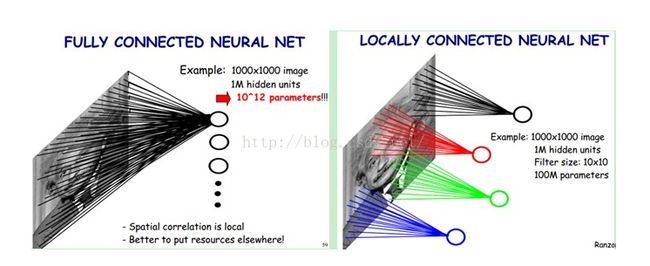
                            图一：全连接和局部连接

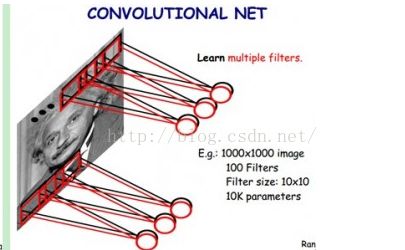
    上图左：全连接网络。如果我们有1000x1000像素的图像，有1百万个隐层神经元，每个隐层神经元都连接图像的每一个像素点，就有1000x1000x1000000=10^12个连接，也就是10^12个权值参数。

   上图右：局部连接网络，每一个节点与上层节点同位置附近10x10的窗口相连接，则1百万个隐层神经元就只有100w乘以100，即10^8个参数。其权值连接个数比原来减少了四个数量级。

    那么问题来了：CNN每个神经元只与上一层一个10x10窗口内的像素点连接，会不会损失数据呢？生物学家通过研究小猫大脑皮层对外界图像刺激的反应做了大量研究，发现大脑皮层每个神经元只感受局部的图像区域，而不需要对全局图像做感受，然后在更高层，将这些感受不同局部的神经元综合起来就可以得到全局的信息了。深度学习本来就是模拟人脑，所以这样做是合理的。

     还有一个问题就是：什么是权值共享，为什么可以权值共享？仍以上图为例，我们用一个10X10的矩阵对输入图像从左上角到右下角依次取10X10的窗口做卷积，这个矩阵就滤波器，它有10X10个参数，如果每次卷积操作的参数不同（滤波器不同），就需要（1000 - 10 + 1）X （1000 - 10 + 1）个滤波器，需要训练的参数个数就是（1000 - 10 + 1）X （1000 - 10 + 1）X100。权值共享就是指我们可以假定这（1000 - 10 + 1）X （1000 - 10 + 1）个滤波器相同，那么我们只需训练100个参数。那么这么做可行吗？研究表明图像特征分布具有均匀性，所以在图像左上角用于抽取某个特征的滤波器，在图像的其他位置，同样可以抽取该特征（比如抽取图像颜色特征）。

4.CNN网络结构

   卷积神经网络是一个多层的神经网络，每层由多个二维平面组成，而每个平面由多个独立神经元组成。

   

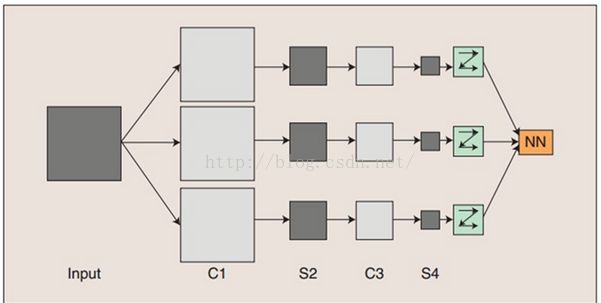
                                                                      图二：卷积神经网络的概念示范

      Input表示原始输入图像，C是特征抽取层（卷积层），S是下采样层（pooling层）。输入的一幅图像，在C1层，通过和3个卷积模板做卷积运算，然后加上偏置值，再经过sigmoid激活函数，得到3个特征映射图，在S2层，对C1层输出的3幅特征映射图做下采样，假设采样因子是2 ，也就是C1层特征图中每2X2的patch中的4个像素抽样出一个像素得到3张尺寸减小了的特征图S2。同样的，再经过C3,S4。将S4的输出拉成一个向量（flatten），输入到传统的神经网络中，并得到输出。

    下面解释下CNN网络结构涉及到的几个概念：

    1）卷积操作：用一个滤波器（就是一个小特征矩阵，也称卷积核）在图像矩阵上游走，在对应位置元素相乘，再把相乘的结果相加，最后相加的结果形成新的图像矩阵，游走完成后即完成了对原始图像的卷积变换（映射变换），形成此滤波器下的特征提取。

     如下图所示，展示了一个3X3的卷积核在5X5的图像上做卷积的过程。每个卷积都是一种特征提取方式（每个卷积核有自己的权重参数，可以提取一种特征），就像一个筛子，将图像中符合条件（激活值越大越符合条件）的部分筛选出来，通过卷积操作，得到一幅3X3的特征图。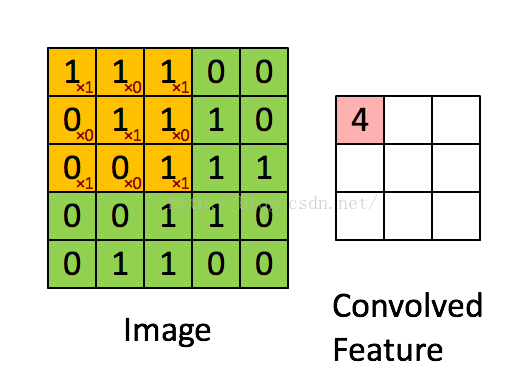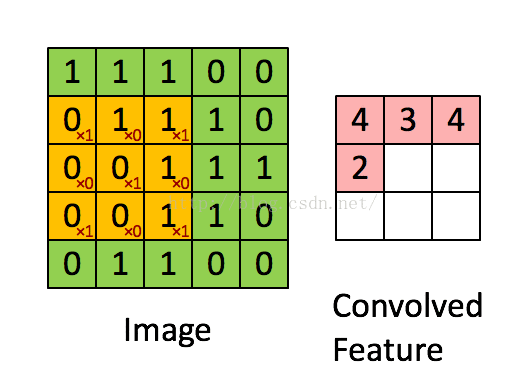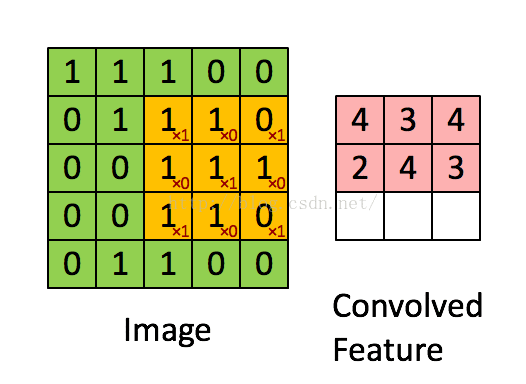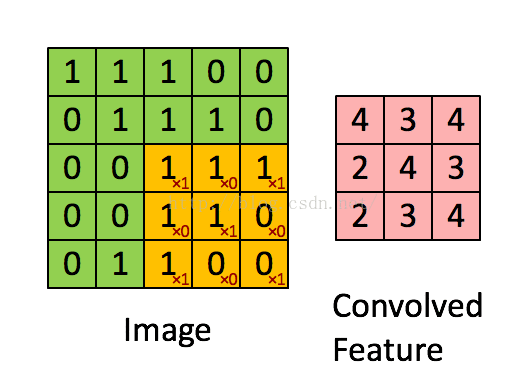   

                                 图三、卷积示意图

       2）多卷积核

      这里还有一个问题就是：每个C层，有多少个卷积核？这个问题可以简单的理解为每个特征核就是一个滤波器，可以抽取一种特种，那么每个C层需要抽取多少种特征，就需要多少个滤波器，即需要多少个特征核，很显然，有多少个卷积核，C层就对应多少幅特征图。实际应用中，每个C层卷积核的个数一般设为32的倍数。这些滤波器的权重参数就是我们训练模型时要求解的参数。

    

                                                                     图四、多卷积核示意图

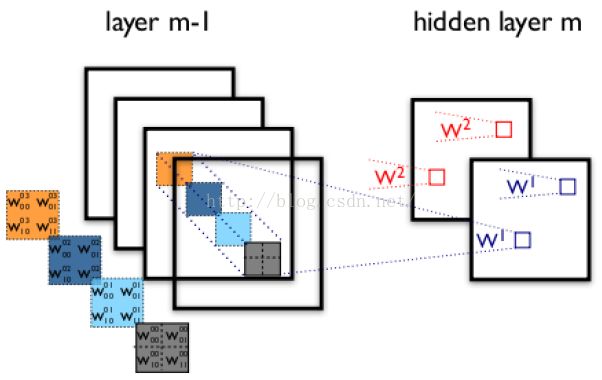
上图中，不同颜色表明不同的卷积核。每个卷积核都会将图像生成为另一幅图像。比如两个卷积核就可以将生成两幅图像，这两幅图像可以看做是一张图像的不同的通道。如下图所示，下图有个小错误，即将w1改为w0，w2改为w1即可。下文中仍以w1和w2称呼它们。下图展示了在四个通道上的卷积操作，有两个卷积核，生成两个通道。其中需要注意的是，四个通道上每个通道对应一个卷积核，先将w2忽略，只看w1，那么在w1的某位置（i,j）处的值，是由四个通道上（i,j）处的卷积结果相加然后再取激活函数值得到的，下图假设激活函数为tanh函数。

                    图五、多通道卷积示意图

      

3）S层的作用

        在通过卷积获得了特征 (features) 之后，下一步我们希望利用这些特征去做分类。理论上讲，人们可以用所有提取得到的特征去训练分类器，例如 softmax 分类器，但这样做面临计算量的挑战。例如：对于一个 96X96 像素的图像，假设我们已经学习得到了400个定义在8X8输入上的特征，每一个特征和图像卷积都会得到一个 (96 ? 8 + 1) × (96 ? 8 + 1) = 7921 维的卷积特征，由于有 400 个特征，所以每个样例 (example) 都会得到一个 892 × 400 = 3,168,400 维的卷积特征向量。学习一个拥有超过 3 百万特征输入的分类器十分不便，并且容易出现过拟合 (over-fitting)。

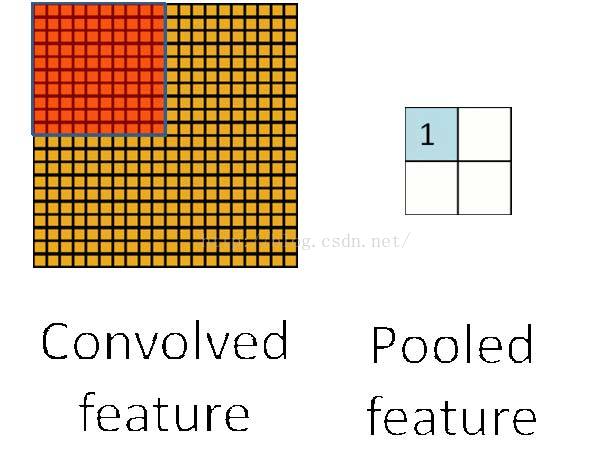
      为了解决这个问题，首先回忆一下，我们之所以决定使用卷积后的特征是因为图像具有一种“静态性”的属性，这也就意味着在一个图像区域有用的特征极有可能在另一个区域同样适用。因此，为了描述大的图像，一个很自然的想法就是对不同位置的特征进行聚合统计，例如，人们可以计算图像一个区域上的某个特定特征的平均值 (或最大值)。这些概要统计特征不仅具有低得多的维度 (相比使用所有提取得到的特征)，同时还会改善结果(不容易过拟合)。这种聚合的操作就叫做池化 (pooling)，有时也称为平均池化或者最大池化 (取决于计算池化的方法)。

                                                                                     图六、池化示意图

     4）感受野和权值共享

      这个问题在第二节CNN网络概述中已经介绍过，这里就不再重复了。

 4.CNN模型训练

     同传统机器学习算法一样，CNN模型训练也 是为了通过训练数据学习模型中的参数，训练算法与传统的BP算法差不多。主要包括4步，这4步被分为两个阶段：

第一阶段，向前传播阶段：

a）从样本集中取一个样本(X,Y_p)，将X输入网络；

b）计算相应的实际输出O_p。

      在此阶段，信息从输入层经过逐级的变换，传送到输出层。这个过程也是网络在完成训练后正常运行时执行的过程。在此过程中，网络执行的是计算（实际上就是输入与每层的权值矩阵相点乘，得到最后的输出结果）：

          O_p=F_n（…（F₂（F₁（X_pW^（1））W^（2））…）W^（n））

第二阶段，向后传播阶段

a）算实际输出O_p与相应的理想输出Y_p的差；

b）按极小化误差的方法反向传播调整权矩阵。

5.用一个简单的例子解释CNN结构

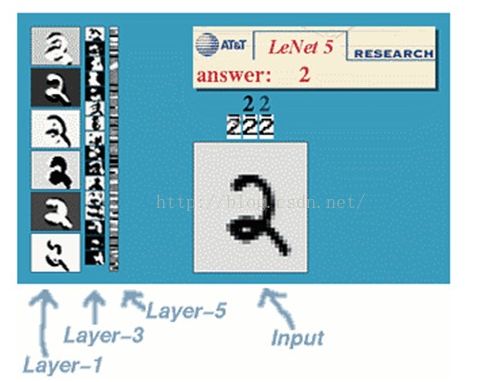
    以网上常见的文字识别系统LeNet-5 网络为例解释CNN网络结构。LeNet-5网络曾被美国很多银行用来识别支票手写数字，这从层面说明该网络的手写数字识别正确率 很高。

                              图七、LeNet-5网络用于手写体数字识别

下图是LeNet-5的卷积网络结构示意图

                                                                                            图八、LeNet-5的卷积网络结构示意图

    LeNet-5共有7层，不包含输入，每层都包含可训练参数（连接权重）。输入图像为32×32大小。这要比Mnist数据库（一个公认的手写数据库，大小应该是28×28）中最大的字母还大。这样做的原因是希望潜在的明显特征如笔画断电或角点能够出现在最高层特征监测子感受野的中心。

    首先，简要解释下上面这个用于文字识别的LeNet-5深层卷积网络：

      1）输入图像的大小是32×32，过滤器的大小是5×5，由于不考虑对图像的边界进行拓展（narrow CNN），则过滤器将有28×28（32 - 5 + 1 = 28，其中1是步长）个不同的位置，也就是C1卷积后得到的特征面的大小是28x28。这里设定C1层中使用6个不同的滤波器，所以C1卷积得有6个不同的特征图，每个特征图使用的滤波器参数相同（权值共享）。
     2）S2层是一个下采样层（subsampling layer）。简单的说，由4个点下采样为1个点，也就是4个数的加权平均。但在LeNet-5系统，下采样层比较复杂，因为这4个加权系数也需要学习得到，这显然增加了模型的复杂度。在斯坦福关于深度学习的教程中，这个过程叫做Pool。S2面的大小是14×14，其中14=28/2。pooling的结果是使得特征减少，参数减少，但pooling的目的并不仅在于此。pooling目的是为了保持某种不变性（旋转、平移、伸缩等），常用的有mean-pooling，max-pooling和Stochastic-pooling三种。
    3）根据前面对C1层的理解，很容易得到C3卷积后特征图的大小为10×10（（14 - 5 + 1）* （14 - 5 + 1））。不同的是c3卷积后得到16个特征图。这里需要注意的是C3每个特征图是有S2层6个特征图任意组合得到的，组合方法在上面的第四部分CNN网络结构中已经介绍过，就不再赘述了，具体到LeNet-5的实现，期组合方式如下表所示：

                                图九、LeNet-5 C3层特征图组合

以c3层的特征图0为例，该特征图组合了s2中0、1、2三张特征图，即该特征图的每一个节点与S2层的第0张特征图，第1张特征图，第2张特征图，总共3个5×5个节点相连接。后面依次类推，C3层每一张特征映射图的权值是相同的。

4.S4 层是在C3层基础上下采样，前面已述。在后面的层由于每一层节点个数比较少，都是全连接层，这个比较简单，不再赘述。