LeetCode 数组 题目总结
2020.2.16
☟☟☟
(1)1.两数之和
题目:给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。
你可以假设每种输入只会对应一个答案。但是,你不能重复利用这个数组中同样的元素。
示例:
给定 nums = [2, 7, 11, 15], target = 9
因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]
暴力法:
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
// int i,j;
int len=nums.size();
for(int i=0;i<len-1;i++){
for(int j=i+1;j<len;j++){
if(nums[i]+nums[j]==target){
return{i,j};//如果找到,就返回
}
}
}
return {};//没有找到返回空数组
}
};
Hash表
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
map<int,int> a;//提供一对一的hash
vector<int> res;//用来承载结果
for(int i=0;i<nums.size();i++)
{ //先找再存,这样有先后关系,在已经存的元素中去找可以凑成2sum对的元素,防止同一个数被使用两次
if(a.count(target-nums[i]))
{
res.push_back(a[target-nums[i]]);
res.push_back(i);
break;
}
a[nums[i]]=i;//反过来放入map中,用来获取结果下标
}
return res;
};
};
☟☟☟
(2)167 两数之和||-输入有序数组
167 Two Sum II - Input array is sorted
给定一个已按照升序排列 的有序数组,找到两个数使得它们相加之和等于目标数。
函数应该返回这两个下标值 index1 和 index2,其中 index1 必须小于 index2。
说明:
返回的下标值(index1 和 index2)不是从零开始的。
你可以假设每个输入只对应唯一的答案,而且你不可以重复使用相同的元素。
示例:
输入: numbers = [2, 7, 11, 15], target = 9
输出: [1,2]
解释: 2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。
思路:双指针,因为是有序的。
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
//vector res;//用vector保存也行
int l=0;
int r=numbers.size()-1;
while(l<r){//从两边开始扫描
if(numbers[l]+numbers[r]<target){
l++;
}
else if(numbers[l]+numbers[r]>target){
r--;
}
else{
return {l+1,r+1};
}
}
return {};
}
};
hash,不快
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
map<int,int> mp;
vector<int> res;
int len=nums.size();
for(int i=0; i<len; i++){
if(mp.count(target-nums[i])){
res.push_back(mp[target-nums[i]]+1);
res.push_back(i+1);
}
mp[nums[i]]=i;
}
return res;
}
};
☟☟☟
(3)15.三数之和
给定一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?找出所有满足条件且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例:
给定数组 nums = [-1, 0, 1, 2, -1, -4],
满足要求的三元组集合为:
[
[-1, 0, 1],
[-1, -1, 2]
]
思路:排序之后用双指针,转化为两数之和问题。
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> res;
vector<int>tmp;
int len=nums.size();
if(len<=2) return res;
sort(nums.begin(),nums.end());//排序
for(int i=0;i<len-2;i++){
if(nums[i]>0){
return res;
}
if(i>0 && nums[i]==nums[i-1]){
continue;
}
int left=i+1,right=len-1;
while(left<right){
if(nums[i]+nums[left]+nums[right]==0){
tmp.push_back(nums[i]);
tmp.push_back(nums[left]);
tmp.push_back(nums[right]);
res.push_back(tmp);
tmp.clear();
while(left<right && nums[left]==nums[left+1]) left++;
while(left<right && nums[right]==nums[right-1]) right--;
//left++;
right--;
}
else if(nums[i]+nums[left]+nums[right]<0){
left++;
}
else{
right--;
}
}
}
return res;
}
};
☺☺☺
(4)16.最接近的三数之和
给定一个包括 n 个整数的数组 nums 和 一个目标值 target。找出 nums 中的三个整数,使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。
例如,给定数组 nums = [-1,2,1,-4], 和 target = 1.
与 target 最接近的三个数的和为 2. (-1 + 2 + 1 = 2).
思路:双指针。排序后! 扫描a[i],后面在用left和right首尾两指针扫描
class Solution {
public:
int threeSumClosest(vector<int>& nums, int target) {
int len=nums.size();
if(len<3) return 0;
sort(nums.begin(),nums.end());
int sum=nums[0]+nums[1]+nums[2];
for(int i=0;i<len-2;i++){
int left=i+1,right=len-1;
while(left<right){
int temp=nums[i]+nums[left]+nums[right];
if(abs(temp-target)<abs(sum-target)){
sum=temp;
}
if(temp<target){
left++;
}
else {
right--;
}
}
}
return sum;
}
};
☺☺☺
(5)18.四数之和
给定一个包含 n 个整数的数组 nums 和一个目标值 target,判断 nums 中是否存在四个元素 a,b,c 和 d ,使得 a + b + c + d 的值与 target 相等?找出所有满足条件且不重复的四元组。
注意:
答案中不可以包含重复的四元组。
示例:
给定数组 nums = [1, 0, -1, 0, -2, 2],和 target = 0。
满足要求的四元组集合为:
[
[-1, 0, 0, 1],
[-2, -1, 1, 2],
[-2, 0, 0, 2]
]
思路:排序,双指针;参照三数之和
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
vector<vector<int>> res;
int len=nums.size();
if(len<4) return res;
sort(nums.begin(),nums.end());//排序
for(int i=0;i<len-3;i++){
if(i>0 && nums[i]==nums[i-1]) continue; //重复
for(int j=i+1; j<len-2;j++){
if(j>i+1 && nums[j]==nums[j-1]) continue; //重复
int left=j+1, right=len-1;
while(left<right){
if(nums[i]+nums[j]+nums[left]+nums[right]==target){
res.push_back({nums[i],nums[j],nums[left],nums[right]});
while(left<right && nums[left+1]==nums[left]) left++; //重复
while(left<right && nums[right-1]==nums[right]) right--; //重复
left++;
}
else if(nums[i]+nums[j]+nums[left]+nums[right]<target){
left++;
}
else{
right--;
}
}
}
}
return res;
}
};
也可以定义一个set,可以避免重复项,记得最后要转化回去
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
//vector> res;
set<vector<int>> res;
int len=nums.size();
if(len<4) return vector<vector<int>>(); //或者用{{}}
sort(nums.begin(),nums.end());//排序
for(int i=0;i<len-3;i++){
//if(i>0 && nums[i]==nums[i-1]) continue;
for(int j=i+1; j<len-2;j++){
//if(j>i+1 && nums[j]==nums[j-1]) continue;
int left=j+1, right=len-1;
while(left<right){
if(nums[i]+nums[j]+nums[left]+nums[right]==target){
vector<int> tmp{nums[i], nums[j], nums[left], nums[right]};
res.insert(tmp); //用set,当有重复结果时,插入会失败
left++;
}
else if(nums[i]+nums[j]+nums[left]+nums[right]<target){
left++;
}
else{
right--;
}
}
}
}
return vector<vector<int>>(res.begin(), res.end()); //由set转化为vector输出
}
};
☺☺☺
(6)217.存在重复元素
给定一个整数数组,判断是否存在重复元素。
如果任何值在数组中出现至少两次,函数返回 true。如果数组中每个元素都不相同,则返回 false。
示例 1:
输入: [1,2,3,1]
输出: true
示例 2:
输入: [1,2,3,4]
输出: false
示例 3:
输入: [1,1,1,3,3,4,3,2,4,2]
输出: true
法1:哈希,判断key值是否大于1
//unordered_map
class Solution {
public:
bool containsDuplicate(vector<int>& nums) {
map<int,int> p;
for(int i=0;i<nums.size();i++){
p[nums[i]]++; //注意后写if条件
if(p[nums[i]]>1){
return true;
}
}
return false;
}
};
法2.利用集合,与原数组比较大小
class Solution {
public:
bool containsDuplicate(vector<int>& nums) {
set<int> st (nums.begin(),nums.end()); //初始化
return (st.size()==nums.size()) ? false:true;
//return nums.size()>st.size();
}
};
法3.排序,比较前后两个元素是否相等,来判断是否存在重复元素
class Solution {
public:
bool containsDuplicate(vector<int>& nums) {
int len=nums.size();
if(len<2) return false;
sort(nums.begin(),nums.end());
for(int i=1; i<nums.size();i++){
if(nums[i]==nums[i-1]){ //注意从1开始
return true;
}
}
return false;
}
};
☺☺☺
(7)26. 删除排序数组中的重复项
给定一个排序数组,你需要在原地删除重复出现的元素,使得每个元素只出现一次,返回移除后数组的新长度。
不要使用额外的数组空间,你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。
示例 1:
给定数组 nums = [1,1,2],
函数应该返回新的长度 2, 并且原数组 nums 的前两个元素被修改为 1, 2。
你不需要考虑数组中超出新长度后面的元素。
示例 2:
给定 nums = [0,0,1,1,1,2,2,3,3,4],
函数应该返回新的长度 5, 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4。
你不需要考虑数组中超出新长度后面的元素。
方法:双指针法(覆盖法);相等时不覆盖,不等时覆盖
设置两个指针,一个慢指针i,一个快指针j,当nums[i]!=nums[j],将nums[i+1]=nums[j]。
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
if(nums.size()==0) return 0;
int i=0;
for(int j=1; j<nums.size(); j++){
if(nums[j]!=nums[i]){
++i;
nums[i]=nums[j];
}
}
return i+1;
}
};
☺☺☺
(8)80. 删除排序数组中的重复项 II 【中等】
给定一个排序数组,你需要在原地删除重复出现的元素,使得每个元素最多出现两次,返回移除后数组的新长度。
不要使用额外的数组空间,你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。
示例 :
给定 nums = [1,1,1,2,2,3],
函数应返回新长度 length = 5, 并且原数组的前五个元素被修改为 1, 1, 2, 2, 3 。
思路:原地删除,用双指针!快指针:遍历整个数组;慢指针:记录可以覆写数据的位置;
当数组的长度小于等于 2 时,不需要操作,直接返回原数组即可。
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
int len=nums.size();
if(len<=2) return len;
int i=1;
for(int j=2; j<len; j++){
if(nums[j]!=nums[i-1]){
i++;
nums[i]=nums[j];
}
}
return i+1;
}
};
☺☺☺
(9)349. 两个数组的交集
给定两个数组,编写一个函数来计算它们的交集。
示例 1:
输入: nums1 = [1,2,2,1], nums2 = [2,2]
输出: [2]
示例 2:
输入: nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出: [9,4]
说明:
输出结果中的每个元素一定是唯一的。
我们可以不考虑输出结果的顺序。
法1:查找,用set避免重复
注意:迭代器 end 指向尾元素的“下一个位置”!
O(n) ,O(n)
class Solution {
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
unordered_set<int> st1(nums1.begin(),nums1.end()); //用unordered_set对nums1的元素去重
unordered_set<int> st2(nums2.begin(),nums2.end());//用unordered_set对nums2的元素去重
vector<int> res;
for(int i:st2){//set不能用下标运算符,所以写成**a:st2**,遍历st2中元素
if(st1.find(i)!=st1.end()){ //必须写**!=st1.end()**
res.push_back(i);
}
}
return res;
}
};
法2:同法1
class Solution {
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
unordered_set<int> m(nums1.begin(), nums1.end()); //将第一个数组的元素建立一个unordered_set
vector<int> res;//建立关于结果的vector
for(int a:nums2) //set不能用下标运算符,所以写成**a:nums2**,遍历nums中元素
{
if( m.count(a)) //查找了m中是否存在a,
{
res.push_back(a);//在vector res的末尾加入a
m.erase(a);//去除该数,//**删除的是m中的元素**
//这里不理解, a是迭代器吗???????和(10)法1比较
//因为在m中删除,所以变成迭代器了???
}
}
return res;
}
};
自我理解上面问题:set里面不需要,vector需要抽象出一个迭代器。
法3:排序后再找
空间换时间
O(nlogn),O(1)
**注意:获取首元素和尾元素最直接的方法是调用 front 和 back **
class Solution {
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
vector<int> res;
sort(nums1.begin(),nums1.end());
sort(nums2.begin(),nums2.end());
int i=0,j=0;
while (i<nums1.size() && j<nums2.size()){
if(nums1[i]<nums2[j]){
i++;
}
else if(nums1[i]>nums2[j]){
j++;
}
else{//==
if(res.empty() || res.back()!=nums1[i]){
res.push_back(nums1[i]);
}
i++;
j++;
}
}
return res;
}
};
细节注意:c.erase(p)是删除迭代器p所指的元素,所以说p是一个迭代器!
set<int> iset={1,2,3,4,5,6,7,8,9,10};
iset.find(1); //返回一个迭代器!!!,指向key==1的元素
iset.find(11); //返回一个迭代器!!!,其值等于iset.end()
iset.count(1); //返回1
iset.count(11); //返回0
☺☺☺
(10)350. 两个数组的交集 II
给定两个数组,编写一个函数来计算它们的交集。
示例 1:
输入: nums1 = [1,2,2,1], nums2 = [2,2]
输出: [2,2]
示例 2:
输入: nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出: [4,9]
说明:
输出结果中每个元素出现的次数,应与元素在两个数组中出现的次数一致。
我们可以不考虑输出结果的顺序。
法1:直接在数组上查找,查找完之后删除
class Solution {
public:
vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
vector<int>::iterator it; //必须先定义迭代器it
vector<int> res;
for(int i:nums1){// i是一个值
it=find(nums2.begin(),nums2.end(),i); //it是一个迭代器
if(it!=nums2.end()){
res.push_back(i); // 或者 res.push_back(*it);
nums2.erase(it); //it是迭代器
}
}
return res;
}
};
排序后再找
class Solution {
public:
vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
if(nums1.empty() || nums2.empty()) return {};
vector<int> res;
sort(nums1.begin(),nums1.end());
sort(nums2.begin(),nums2.end());
int i=0,k=0;
while( i<nums1.size() && k<nums2.size() )
{
if(nums1[i]==nums2[k])
{
res.push_back(nums1[i]);
i++;
k++;
}
else if(nums1[i]>nums2[k])
k++;
else
i++;
}
return res;
}
};
法3:hash表
**思路:此题可以看成是一道传统的映射题(map映射),为什么可以这样看呢,因为我们需找出两个数组的交集元素,同时应与两个数组中出现的次数一致。这样就导致了我们需要知道每个值出现的次数,所以映射关系就成了<元素,出现次数>,所以我们可以首先统计数组1中所有元素的出现次数。然后再遍历数组2,如果数组2中的元素在map中存在(出现次数大于0),该元素就是一个交集元素,我们就将其存入返回数组中并且将map中该元素的出现次数减一即可.
**
class Solution {
public:
vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
map<int,int> map;
vector<int> res;
for(int i=0; i<nums1.size(); i++){
map[nums1[i]]++;
}
for(int i=0; i<nums2.size(); i++){
if(map[nums2[i]]>0){
res.push_back(nums2[i]);
map[nums2[i]]--;
}
}
return res;
}
};
☺☺☺
(11)228. 汇总区间
给定一个无重复元素的有序整数数组,返回数组区间范围的汇总。
示例 1:
输入: [0,1,2,4,5,7]
输出: [“0->2”,“4->5”,“7”]
解释: 0,1,2 可组成一个连续的区间; 4,5 可组成一个连续的区间。
示例 2:
输入: [0,2,3,4,6,8,9]
输出: [“0”,“2->4”,“6”,“8->9”]
解释: 2,3,4 可组成一个连续的区间; 8,9 可组成一个连续的区间。
思路:双指针
因为题目强调的是连续的区间,所以可用如下方法。第二指针结束位置:区间右端
class Solution {
public:
vector<string> summaryRanges(vector<int>& nums) {
vector<string> res;
if(nums.empty()){
return res;
}
for(int i=0; i<nums.size();){ //注意写 ;
int left=i;
int right=i;
while(right+1<nums.size() && nums[right+1]==nums[right]+1){
right++;
}
if(right-left==0){
res.push_back(to_string(nums[right]));
}
else if(right-left>0){
res.push_back(to_string(nums[left])+"->"+ to_string(nums[right]));
}
i=right+1;
}
return res;
}
};
注意:写成这样会超时:
while(right+1<nums.size() && nums[right+1]-nums[right]==1){
right++;
}
方法同上:
class Solution {
public:
vector<string> summaryRanges(vector<int>& nums) {
vector<string> res;
if(!nums.empty()){
long i = 0, j = 0;
while(j < nums.size()){
while(j < nums.size()-1 && nums[j+1] == nums[j]+1) j++;
if(j == i){
res.push_back(to_string(nums[i]));
}
if(j > i) res.push_back(to_string(nums[i])+"->"+to_string(nums[j]));
i = j + 1;
j = i;
}
}
return res;
}
};
☺☺☺
(12)334. 递增的三元子序列
给定一个未排序的数组,判断这个数组中是否存在长度为 3 的递增子序列。
数学表达式如下:
如果存在这样的 i, j, k, 且满足 0 ≤ i < j < k ≤ n-1,
使得 arr[i] < arr[j] < arr[k] ,返回 true ; 否则返回 false 。
说明: 要求算法的时间复杂度为 O(n),空间复杂度为 O(1) 。
示例 1:
输入: [1,2,3,4,5]
输出: true
示例 2:
输入: [5,4,3,2,1]
输出: false
注意:可以是不连续的数,比如[2,1,5,0,4,6]也返回true
思路:双指针。。。长度为3意思是连续的3个数,[2,1,5,0,4,6]结果是[0,4,6]
m1, m2保存两个较小数,找出一个同时大于m1和m2的数即返回。
时间复杂度:O(n)
空间复杂度:O(1)
class Solution {
public:
bool increasingTriplet(vector<int>& nums) {
int m1 = INT_MAX, m2 = INT_MAX;
for (auto a : nums) {
if (a<=m1) m1 = a; //a为扫描过程中遇到的最小数,是第一个数的候选
else if (a<=m2) m2 = a;//当a 大于m1,a可能是第二或第三个数
else return true; // m1
}
return false;
}
};
☺☺☺
(13)66. 加一
给定一个由整数组成的非空数组所表示的非负整数,在该数的基础上加一。
最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。
你可以假设除了整数 0 之外,这个整数不会以零开头。
示例 1:
输入: [1,2,3]
输出: [1,2,4]
解释: 输入数组表示数字 123。
示例 2:
输入: [4,3,2,1]
输出: [4,3,2,2]
解释: 输入数组表示数字 4321。
/*
问题:数组加一,高位在前,低位在后
要考虑进位情况
*/
class Solution {
public:
vector<int> plusOne(vector<int>& digits) {
//123 129 199 999
for(int i=digits.size()-1; i>=0; i--){//从后往前扫描
if(digits[i]==9){//如果为9,置0,下次进位
digits[i]=0;
}
else{
digits[i]++;
return digits;//不为9就加一,退出
}
}
digits[0]=1;//如果最高位有进位,置1
digits.push_back(0); //补充一位
return digits;
}
};
☟☟☟
(14)283. 移动零
知识点:c.erase(p) 删除迭代器p所指定的元素,返回一个指向被删除元素之后的迭代器(注意是 之后!);若p指向尾元素,则返回尾后迭代器。
c.push_back(t) 在c的尾部创建一个值为t的元素,返回void;
c.insert(p,t) 在迭代器p指向的元素之前创建一个值为t的元素。返回指向新添加的元素的迭代器; c.inert(p,n,t) 在迭代器p指向的元素之前插入n个值为t的元素。返回指向新添加的第一个元素的迭代器。
题目:
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
示例:
输入: [0,1,0,3,12]
输出: [1,3,12,0,0]
说明:
必须在原数组上操作,不能拷贝额外的数组。
尽量减少操作次数
法1:遍历数组,只要遇到0则删除,count加1(计0的个数),最后在末尾补上count个0即可。因为使用了迭代器,要注意的是避免迭代器失效。
方法不咋地,但是能学会运用不少东西啊,比如迭代器。
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int count=0;
for (auto it=nums.begin(); it!=nums.end();){
if(*it==0){
it=nums.erase(it);
count++;
}
else it++;
}
while(count>0){
nums.push_back(0);
//nums.insert(nums.end(),0);
count--;
}
//nums.insert(nums.end(),count,0);//可以用这个代替上面的while循环
}
};
法2:双指针
✘错误代码
原因:int i 定义到了for循环里面,是局部变量,当第一个for循环结束,i就不存在了。
class Solution {
public:
void moveZeroes(vector<int>& nums) {
//int i=0;
for(int i=0; i<nums.size() && nums[i]!=0; ++i);//
for(int j=i+1; j<nums.size(); j++){
if(nums[j]!=0){
swap(nums[i],nums[j]);
++i;
}
}
}
};
**正确代码,定义全局变量i **
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int i=0;
for(i=0; i<nums.size() && nums[i]!=0; ++i);////找到第一个0;
for(int j=i+1; j<nums.size(); j++){//将第一个零之后的第一个非零数字与该0交换
if(nums[j]!=0){
swap(nums[i],nums[j]);
++i;
}
}
}
};
☟☟☟
(15)36. 有效的数独 【中等】
判断一个 9x9 的数独是否有效。只需要根据以下规则,验证已经填入的数字是否有效即可。
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

上图是一个部分填充的有效的数独。
数独部分空格内已填入了数字,空白格用 ‘.’ 表示。
示例 1:
输入:
[
["5","3",".",".","7",".",".",".","."],
["6",".",".","1","9","5",".",".","."],
[".","9","8",".",".",".",".","6","."],
["8",".",".",".","6",".",".",".","3"],
["4",".",".","8",".","3",".",".","1"],
["7",".",".",".","2",".",".",".","6"],
[".","6",".",".",".",".","2","8","."],
[".",".",".","4","1","9",".",".","5"],
[".",".",".",".","8",".",".","7","9"]
]
输出: true
示例 2:
输入:
[
["8","3",".",".","7",".",".",".","."],
["6",".",".","1","9","5",".",".","."],
[".","9","8",".",".",".",".","6","."],
["8",".",".",".","6",".",".",".","3"],
["4",".",".","8",".","3",".",".","1"],
["7",".",".",".","2",".",".",".","6"],
[".","6",".",".",".",".","2","8","."],
[".",".",".","4","1","9",".",".","5"],
[".",".",".",".","8",".",".","7","9"]
]
输出: false
解释: 除了第一行的第一个数字从 5 改为 8 以外,空格内其他数字均与 示例1 相同。
但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。
说明:
一个有效的数独(部分已被填充)不一定是可解的。
只需要根据以上规则,验证已经填入的数字是否有效即可。
给定数独序列只包含数字 1-9 和字符 '.' 。
给定数独永远是 9x9 形式的。
法1:暴力!先按行排查,再按列排查,最后按3*3排查。具体实现采用了辅助数组a[10]来统计0-9出现的次数,若a[x]>1,则返回false。
因为要存放数字1-9,最大要到9的位置,所以定义数组大小为a[10],下标为0~9
class Solution {
public:
bool isValidSudoku(vector<vector<char>>& board) {
//先按照行排查
for(int i=0;i<9;++i){
int a[10]={0,0,0,0,0,0,0,0,0,0};
for(int j=0;j<9;++j){
if(board[i][j]=='.') continue;
a[board[i][j]-'0']+=1;
if(a[board[i][j]-'0']>1) return false;
}
}
//按列排查
for(int j=0;j<9;++j){
int a[10]={0,0,0,0,0,0,0,0,0,0};
for(int i=0;i<9;++i){
if(board[i][j]=='.') continue;
a[board[i][j]-'0']+=1;
if(a[board[i][j]-'0']>1)return false;
}
}
//按照3*3排查
for(int i=0;i<9;i=i+3){
for(int j=0;j<9;j=j+3){
int a[10]={0,0,0,0,0,0,0,0,0,0};
for(int x=i;x<i+3;x++){
for(int y=j;y<j+3;y++){
if(board[x][y]=='.') continue;
a[board[x][y]-'0']+=1;
if(a[board[x][y]-'0']>1)return false;
}
}
}
}
return true;
}
};
法2:这个解法有点烧脑!!!
class Solution {
public:
bool isValidSudoku(vector<vector<char>>& board) {
int row[9][10] = {0};// 哈希表存储每一行的每个数是否出现过,默认初始情况下,每一行每一个数都没有出现过
// 整个board有9行,第二维的维数10是为了让下标有9,和数独中的数字9对应。
int col[9][10] = {0};// 存储每一列的每个数是否出现过,默认初始情况下,每一列的每一个数都没有出现过
int box[9][10] = {0};// 存储每一个box的每个数是否出现过,默认初始情况下,在每个box中,每个数都没有出现过。整个board有9个box。
for(int i=0; i<9; i++){
for(int j = 0; j<9; j++){
// 遍历到第i行第j列的那个数,我们要判断这个数在其所在的行有没有出现过,
// 同时判断这个数在其所在的列有没有出现过
// 同时判断这个数在其所在的box中有没有出现过
if(board[i][j] == '.') continue;
int curNumber = board[i][j]-'0';
if(row[i][curNumber]) return false;
if(col[j][curNumber]) return false;
if(box[j/3 + (i/3)*3][curNumber]) return false;
row[i][curNumber] = 1;// 之前都没出现过,现在出现了,就给它置为1,下次再遇见就能够直接返回false了。
col[j][curNumber] = 1;
box[j/3 + (i/3)*3][curNumber] = 1;
}
}
return true;
}
};
☟☟☟
(16)48. 旋转图像
给定一个 n × n 的二维矩阵表示一个图像。
将图像顺时针旋转 90 度。
说明:
你必须在原地旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。
示例 1:
给定 matrix =
[
[1,2,3],
[4,5,6],
[7,8,9]
],
原地旋转输入矩阵,使其变为:
[
[7,4,1],
[8,5,2],
[9,6,3]
]
示例 2:
给定 matrix =
[
[ 5, 1, 9,11],
[ 2, 4, 8,10],
[13, 3, 6, 7],
[15,14,12,16]
],
原地旋转输入矩阵,使其变为:
[
[15,13, 2, 5],
[14, 3, 4, 1],
[12, 6, 8, 9],
[16, 7,10,11]
]
顺时针旋转矩阵:先上下翻转,再沿对角线翻转
//问题:旋转图像(要求:原地顺时针旋转90°)
/*
* 顺时针旋转方法:先上下翻转,再沿对角线翻转
* clockwise rotate
* first reverse up to down, then swap the symmetry
* 1 2 3 7 8 9 7 4 1
* 4 5 6 => 4 5 6 => 8 5 2
* 7 8 9 1 2 3 9 6 3
*/
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
reverse(matrix.begin(), matrix.end()); //stl中翻转数组,对每列reverse,直接reverse matrix即可
for(int i=0; i<matrix.size(); i++){//只需对一半元素执行操作
for(int j=i+1; j<matrix[0].size(); j++){
swap(matrix[i][j],matrix[j][i]);
}
}
}
};
逆时针旋转矩阵:先左右翻转,再沿对角线翻转
/*
* * 逆时针旋转方法:先左右翻转,再沿对角线翻转
* anticlockwise rotate
* first reverse left to right, then swap the symmetry
* 1 2 3 3 2 1 3 6 9
* 4 5 6 => 6 5 4 => 2 5 8
* 7 8 9 9 8 7 1 4 7
*/
void anti_rotate(vector<vector<int> > &matrix) {
for (auto vi : matrix) reverse(vi.begin(), vi.end()); //对每行reverse,故要遍历matrix,reverse内部容器
for (int i = 0; i < matrix.size(); ++i) {
for (int j = i + 1; j < matrix[i].size(); ++j)
swap(matrix[i][j], matrix[j][i]);
}
}
☟☟☟
(17)面试题57. 和为s的两个数字
输入一个递增排序的数组和一个数字s,在数组中查找两个数,使得它们的和正好是s。如果有多对数字的和等于s,则输出任意一对即可。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[2,7] 或者 [7,2]
示例 2:
输入:nums = [10,26,30,31,47,60], target = 40
输出:[10,30] 或者 [30,10]
思路:双指针
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
vector<int> res;
int left=0, right=nums.size()-1;
while(left < right){
if(nums[left]+nums[right]==target){
res.push_back(nums[left]);
res.push_back(nums[right]);
break; //找到了, 就弹出
}
else if(nums[left]+nums[right] < target) left++;
else right--;
}
return res;
}
};
如果题目要求输出乘积最小的,如下:
题目描述
输入一个递增排序的数组和一个数字S,在数组中查找两个数,使得他们的和正好是S,如果有多对数字的和等于S,输出两个数的乘积最小的。
则,思路也一样,因为:
不要被题目误导了!证明如下,清晰明了:
//输出两个数的乘积最小的。这句话的理解?
假设:若b>a,且存在,
a + b = s;
(a - m ) + (b + m) = s
则:(a - m )(b + m)=ab - (b-a)m - m*m < ab;说明外层的乘积更小
class Solution {
public:
vector<int> FindNumbersWithSum(vector<int> array,int sum) {
vector<int> result;
int size=array.size();
int left=0;
int right=size-1;
while(right>left){
if(array[left]+array[right]==sum){
result.push_back(array[left]);
result.push_back(array[right]);
break;
}
else if(array[left]+array[right]<sum){
left++;
}
else{
right--;
}
}
return result;
}
};
也贴上这个代码吧,万一人家要求输出乘积最大的呢。变一下下面的符号就行。
//双指针
class Solution {
public:
vector<int> FindNumbersWithSum(vector<int> array,int sum) {
vector<int> ret;
int i = 0, j = array.size()-1;
while(i < j){
if(array[i] + array[j] == sum){
if(ret.empty()){
ret.push_back(array[i]);
ret.push_back(array[j]);
}
else if(array[i]*array[j] < ret[0]*ret[1]){
ret[0] = array[i];
ret[1] = array[j];
}
++i;
--j;
}
else if(array[i] + array[j] < sum) ++i;
else --j;
}
return ret;
}
};
☟☟☟
(18)面试题57 - II. 和为s的连续正数序列
输入一个正整数 target ,输出所有和为 target 的连续正整数序列(至少含有两个数)。
序列内的数字由小到大排列,不同序列按照首个数字从小到大排列。
示例 1:
输入:target = 9
输出:[[2,3,4],[4,5]]
示例 2:
输入:target = 15
输出:[[1,2,3,4,5],[4,5,6],[7,8]]
求连续数和
等差数列公式:和 = n(a1+an)/2
思路:双指针
class Solution {
public:
vector<vector<int>> findContinuousSequence(int target) {
vector<vector<int>> res;
int small=1; //正整数,从1开始
int big=2;
while(small<big){
int sum=(big-small+1)*(big+small)/2; //等差数列
if(sum==target){
vector<int> tmp;
for(int i=small; i<=big; i++){ //每个数都放入
tmp.push_back(i);
}
res.push_back(tmp);
big++; //或small++;
}
else if(sum< target) big++;
else if(sum> target) small++;
}
return res;
}
};
☟☟☟
(19)面试题04. 二维数组中的查找
在一个 n * m 的二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
示例:
现有矩阵 matrix 如下:
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]
给定 target = 5,返回 true。
给定 target = 20,返回 false。
思路:定位到右上角。从右上角开始比较,比它大就往下数一行,比它小就往左数一列
class Solution {
public:
bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
if(matrix.size()==0 || matrix[0].size()==0) return false;//记得写
int row=0;
int col=matrix[0].size()-1; //定位到右上角
while(row < matrix.size() && col>=0){//边界条件
if(matrix[row][col]==target) return true;
else if(matrix[row][col] < target) row++;//如果当前位置元素比target小,则row++
else if(matrix[row][col] > target) col--;//如果当前位置元素比target大,则col--
}
return false;
}
};
☟☟☟
(20)面试题03. 数组中重复的数字
找出数组中重复的数字。
在一个长度为 n 的数组 nums 里的所有数字都在 0~n-1 的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。
示例 1:
输入:
[2, 3, 1, 0, 2, 5, 3]
输出:2 或 3
法1:用一个数组存放出现的次数
class Solution {
public:
int findRepeatNumber(vector<int>& nums) {
int n=nums.size();
vector<int> index(n,0);
int res;
for(int i=0; i<n; i++){
index[nums[i]]++;
if(index[nums[i]]>1){
res= nums[i]; //保存在全局变量,如果用局部变量,当退出for循环后,res也会消失
break;
}
}
return res;
}
};
法2:hash
其实和法1是一样的,把hash表理解成法1的数组。
class Solution {
public:
int findRepeatNumber(vector<int>& nums) {
int n=nums.size();
map<int,int>m;
int res;
for(int i=0; i<n; i++){
m[nums[i]]++;
if(m[nums[i]]>1){
res= nums[i]; //保存在全局变量,如果用局部变量,当退出for循环后,res也会消失
break;
}
}
return res;
}
};
☟☟☟
(21)面试题39. 数组中出现次数超过一半的数字
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入: [1, 2, 3, 2, 2, 2, 5, 4, 2]
输出: 2
解法一:排序取中位数
//时间O(nlogn),空间O(1)
class Solution {
public:
int majorityElement(vector<int>& nums) {
sort(nums.begin(), nums.end());
return nums[nums.size()/2];
}
};
解法二:建立哈希表法
//时间O(n),空间O(n)
class Solution {
public:
int majorityElement(vector<int>& nums) {
map<int,int> m;
int res;//定义全局变量
for(int i=0; i<nums.size(); i++){
m[nums[i]]++;
if(m[nums[i]]>nums.size()/2){//不必等到哈希表完全建立再进行此判断
res=nums[i];
}
}
return res;
}
};
解法3:摩尔投票法
核心理念为 “正负抵消” 。时间复杂度为 O(N) ,空间复杂度为 O(1) 。是本题的最佳解法。
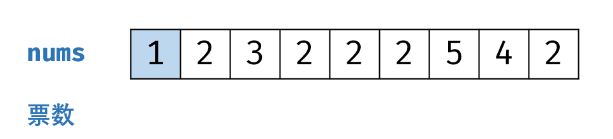
如果有符合条件的数字,则它出现的次数比其他所有数字出现的次数和还要多。
在遍历数组时保存两个值:一是数组中一个数字,一是次数。遍历下一个数字时,若它与之前保存的数字相同,则次数加1,否则次数减1;若次数为0,则保存下一个数字,并将次数置为1。遍历结束后,所保存的数字即为所求。
class Solution {
public:
int majorityElement(vector<int>& numbers) {
int n = numbers.size();
if (n == 0) return 0;
int num = numbers[0], count = 1;
for (int i = 1; i < n; i++) {
if (numbers[i] == num) count++;
else count--;
if (count == 0) {
num = numbers[i];
count = 1;
}
}
return num;
}
};
☟☟☟
(22)面试题53 - I. 在排序数组中查找数字 I(统计一个数字在排序数组中出现的次数。)
统计一个数字在排序数组中出现的次数。
示例 1:
输入: nums = [5,7,7,8,8,10], target = 8
输出: 2
示例 2:
输入: nums = [5,7,7,8,8,10], target = 6
输出: 0
法1:二分查找(面试官要的)
** 二分查找,通过两次二分查找,分别找到第一个k和最后一个k,可以使时间复杂度减少为O(logn)**
class Solution {
public:
int search(vector<int>& nums, int target) {
int first= findFirst(nums, target);
int last=findLast(nums,target);
if(first==-1 || last==-1)
return 0;
return last-first+1;//计算次数
}
int findFirst(vector<int>& nums, int target){
int left=0, right=nums.size()-1;
while(left <= right){
int mid=left+(right-left)/2;
if(nums[mid] < target){
left++;
}
else if(nums[mid] > target){
right--;
}
else if(mid-1>=0 && nums[mid-1]==target){
right=mid-1;
}
else
return mid;
}
return -1;
}
int findLast(vector<int>& nums, int target){
int left=0, right=nums.size()-1;
while(left <= right){
int mid=left+(right-left)/2;
if(nums[mid] < target){
left++;
}
else if(nums[mid] > target){
right--;
}
else if(mid+1<nums.size() && nums[mid+1]==target){
left=mid+1;
}
else
return mid;
}
return -1;
}
};
其他:简单暴力,不是面试官想要的;
法2:
class Solution {
public:
int GetNumberOfK(vector<int> data ,int k) {
return count(data.begin(),data.end(),k);
}
};
法3:
//利用C++ stl的二分查找
class Solution {
public:
int GetNumberOfK(vector<int> data ,int k) {
auto resultPair = equal_range(data.begin(), data.end(),k);
return resultPair.second - resultPair.first;
}
};
法4:
class Solution {
public:
int GetNumberOfK(vector<int> data ,int k) {
int num=0;
for(int i=0;i<data.size();i++){
if(data[i]==k)
num++;
}
return num;
}
};
☟☟☟
(23)面试题53 - II. 0~n-1中缺失的数字
一个长度为n-1的递增排序数组中的所有数字都是唯一的,并且每个数字都在范围0~n-1之内。在范围0~n-1内的n个数字中有且只有一个数字不在该数组中,请找出这个数字。
示例 1:
输入: [0,1,3]
输出: 2
示例 2:
输入: [0,1,2,3,4,5,6,7,9]
输出: 8
二分!!! 排序数组中的搜索问题,首先想到 二分法 解决。
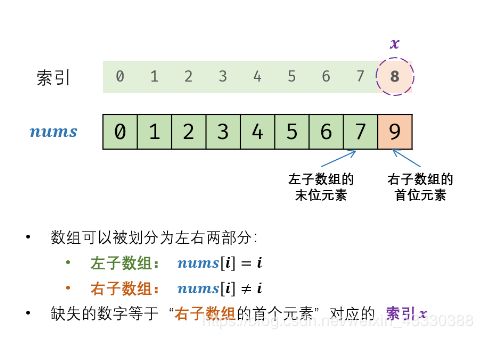
根据题意,数组可以按照以下规则划分为两部分。
左子数组: nums[i]=i ;
右子数组: nums[i]!=i ;
缺失的数字等于 “右子数组的首位元素” 对应的索引;因此考虑使用二分法查找 “右子数组的首位元素” 。
class Solution {
public:
//二分
int missingNumber(vector<int>& nums) {
int left=0;
int right=nums.size()-1;
while(left<=right){
int mid=left+(right-left)/2;
if(nums[mid]==mid){
left=mid+1;
}
else // !=
right=mid-1;
}
return left;
}
};
☟☟☟
(24)面试题66:构建乘积数组
给定一个数组 A[0,1,…,n-1],请构建一个数组 B[0,1,…,n-1],其中 B 中的元素 B[i]=A[0]×A[1]×…×A[i-1]×A[i+1]×…×A[n-1]。不能使用除法。
示例:
输入: [1,2,3,4,5]
输出: [120,60,40,30,24]
思路:
B[i]的值可以看作下图的矩阵中每行的乘积。
下三角用连乘可以很容求得,上三角,从下向上也是连乘。
因此我们的思路就很清晰了,先算下三角中的连乘,即我们先算出B[i]中的一部分,然后倒过来按上三角中的分布规律,把另一部分也乘进去。

class Solution {
public:
vector<int> constructArr(vector<int>& a) {
int n=a.size();
vector<int> b(n);
if(n!=0){
b[0]=1; //计算下三角连乘
for(int i=1; i<n; i++){
b[i]=b[i-1]*a[i-1];
}
//计算上三角
int tmp=1;
for(int j=n-2; j>=0; j--){
tmp=tmp*a[j+1];
b[j]=b[j]*tmp;
}
}
return b;//从B[0]~B[n-1]
}
};
☟☟☟
(25)面试题21. 调整数组顺序使奇数位于偶数前面
输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有奇数位于数组的前半部分,所有偶数位于数组的后半部分。
示例:
输入:nums = [1,2,3,4]
输出:[1,3,2,4]
注:[3,1,2,4] 也是正确的答案之一。
法1思路:首尾双指针
定义头指针 left ,尾指针 right .
left 一直往右移,直到它指向的值为偶数
right 一直往左移, 直到它指向的值为奇数
交换 nums[left] 和 nums[right] .
重复上述操作,直到 left == rightleft==right .
class Solution {
public:
vector<int> exchange(vector<int>& nums) {
// if (nums.empty()) return nums;
int l = 0, r = nums.size() - 1;
while (l < r) {
while (l < r && nums[l] % 2 == 1) ++l;
while (l < r && nums[r] % 2 == 0) --r;
swap(nums[l], nums[r]);
}
return nums;
}
};
法2: 用一个新数组保存 low
class Solution {
public: //评论里说此方法有点low!
void reOrderArray(vector<int> &array) {
vector<int> res;
for(int i = 0; i < array.size(); i++)
{
if(array[i] % 2 == 1)
res.push_back(array[i]);
}
for(int i = 0; i < array.size(); i++)
{
if(array[i] % 2 == 0)
res.push_back(array[i]);
}
//array.swap(res);
array = res;
}
};
法3(没看):插入算法思想,先把当前的数保存,整体后移。。
class Solution {
public:
//插入排序思想
void reOrderArray(vector<int> &array) {
int size=array.size();
for(int i=0;i<size;i++){
int target = array[i];
if(array[i] % 2 == 1){
int j = i;
while(j >= 1 && array[j-1] % 2 == 0){
array[j] = array[j-1];
j--;
}
array[j] = target;
}
}
}
};
☟☟☟
(26)面试题61. 扑克牌中的顺子
从扑克牌中随机抽5张牌,判断是不是一个顺子,即这5张牌是不是连续的。2~10为数字本身,A为1,J为11,Q为12,K为13,而大、小王为 0 ,可以看成任意数字。A 不能视为 14。
示例 1:
输入: [1,2,3,4,5]
输出: True
示例 2:
输入: [0,0,1,2,5]
输出: True
思路:排序后,求出0的数量,求出空的间隔数,比较它们
class Solution {
public:
bool isStraight(vector<int>& nums) {
int size=nums.size();
//if(size<=0) return false;//没有扑克
sort(nums.begin(), nums.end());//注意排序
int numof0=0;//0的数量
for(int i=0; i<size; i++){
if(nums[i]==0) numof0++;
}
int kong=0;//空格数量
for(int i=numof0+1; i<size; i++){
if(nums[i]==nums[i-1]) return false;
else kong += nums[i]-nums[i-1]-1;
}
if(numof0 >= kong) return true;
else return false;
}
};
知识点:sort
c++中的sort函数和实例
sort中的比较函数compare要声明为静态成员函数或全局函数,不能作为普通成员函数,否则会报错。 因为:非静态成员函数是依赖于具体对象的,而std::sort这类函数是全局的,因此无法再sort中调用非静态成员函数。静态成员函数或者全局函数是不依赖于具体对象的, 可以独立访问,无须创建任何对象实例就可以访问。同时静态成员函数不可以调用类的非静态成员。
通俗说明用法:
c++中的sort函数一般用来对数组进行排序,有三个参数,第一个参数是是数组的起始位子,第二个参数为你要排序的数组的终止位子。
第三个参数一般是排序的条件,可以通过这个参数达到各种各样的排序(后面再讲),也可以不写,默认是升序。
如:int arr[5]={1,3,2,5,4}. 操作:sort(arr,arr+5). 结果{1,2,3,4,5} //默认升序
如: int arr[5]={1,3,2,5,3}. 操作:sort(arr,arr+3) 结果{1,2,3,5,4} //对数组可以部分操作
这里我对第三个参数进行详细解释:第三个参数可以是一个函数,如果该函数返回为真,就将操作对象位子不变,否则交换位子(后面有例子)。
我们可以通过调整该函数的内容来控制,当某个条件满足时返回值的真假。
如:例如一个数组{32,3}这两个数如何拼接组合达到的数最小,两种情况323,332。显然323小。这类问题可以用sort来进行操作。
代码如下:
int arr[3]={3,32,321} // 组成最小数是321323
sort(arr,arr+3,cmp). //对数组三个位子进行操作,条件是cmp函数,一般是bool类型函数
static bool cmp(int a, int b)
{
string A = to_string(a)+to_string(b);
string B =to_string(b)+to_string(a);
return A<B;
}
//函数的意思是sort函数操作的对象数组中两个挨着的顺序的元素,分别赋值到a和b上。
通过一系列操作,满足条件某个条件(题中条件是A<B),返回如果真,两个数顺序不变,如果返回假,两个元素交换位子。
详细解读上面得到最小值321323的过程:
从sort函数开始,将数组前两个值3,32丢入cmp中。即a=3,b=32.先将a和b转换成字符串
再拼接故A=“332” B=“323” 故return A<B这个条件是假值,sort函数将这两个值的位子交换。此时arr={32,3,321}.
接下来类似操作依次得到结果是:
arr={32,321,3}
arr={321,32,3}。
将上述数组遍历输出及得到结果。(到这里sort内容讲完)
☟☟☟
(27)面试题45. 把数组排成最小的数
输入一个正整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。
示例 1:
输入: [10,2]
输出: "102"
示例 2:
输入: [3,30,34,5,9]
输出: "3033459"
思路:sort(第三个参数排序)
class Solution {
public:
string minNumber(vector<int>& nums) {
int len=nums.size();
if(len==0) return "";
string res;
sort(nums.begin(), nums.end(), cmp);
for(int i=0; i<len; i++){
res += to_string(nums[i]); //所以这里还得to_string
}
return res;
}
//是的,必须 static
static bool cmp(int a, int b){//只是交换了原数组中的位置,并没有把它们变成string
string A=to_string(a)+to_string(b);
string B=to_string(b)+to_string(a);
return A<B;
}
};
☟☟☟
(28)剑指11.旋转数组的最小数字(189. Rotate Array)【该题归类到了查找与排序(二分)】
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个递增排序的数组的一个旋转,输出旋转数组的最小元素。例如,数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一个旋转,该数组的最小值为1。
示例 1:
输入:[3,4,5,1,2]
输出:1
示例 2:
输入:[2,2,2,0,1]
输出:0
思路:二分查找
该题减治的思想是:通过排除不可能是最小值元素,进而缩小范围。
当我们拿中间的数和最右边的数相比时,有三种情况:
1. 中间的数比右边的大,那么中间数不可能是最小的数,
最小的数只可能出现在中间数的后面,改left = mid + 1缩小区间
3. 中间的数和右边的小,那么右边的数不可能是中位数,
此时,中间的数可能是最小的数,改right = mid 缩小区间
5. 中间的数和右边相等,例如[3,3,3,1,3]此时中间的数和最右边的数都为3,
可以知道的是,此时我们可以排除最右边的数,改区间为right = right - 1
class Solution {
public:
int minArray(vector<int>& numbers) {
int i=0, j=numbers.size()-1;
while(i < j){ //当i=j时,跳出循环,返回i所指元素
int m=i + (j - i) / 2;//int m=(i+j)/2;
if(numbers[m]>numbers[j]) i=m+1;
else if(numbers[m] < numbers[j]) j=m;
else j--;
}
return numbers[i];
}
};
while (i < j) 循环里应该是<=吧。请问为什么是<
☟☟☟
(29)面试题51. 数组中的逆序对【困难】
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
示例 1:
输入: [7,5,6,4]
输出: 5
思路:归并排序
貌似是剑指最难的一道,看了半天放弃了。这里先贴一个可通过的代码。复习了排序算法再返回来看。
class Solution {
public:
int InversePairs(vector<int> data) {
int length=data.size();
if(length<=0)
return 0;
//vector copy=new vector[length];
vector<int> copy;
for(int i=0;i<length;i++)
copy.push_back(data[i]);
long long count=InversePairsCore(data,copy,0,length-1);
//delete[]copy;
return count%1000000007;
}
long long InversePairsCore(vector<int> &data,vector<int> ©,int start,int end)
{
if(start==end)
{
copy[start]=data[start];
return 0;
}
int length=(end-start)/2;
long long left=InversePairsCore(copy,data,start,start+length);
long long right=InversePairsCore(copy,data,start+length+1,end);
int i=start+length;
int j=end;
int indexcopy=end;
long long count=0;
while(i>=start&&j>=start+length+1)
{
if(data[i]>data[j])
{
copy[indexcopy--]=data[i--];
count=count+j-start-length; //count=count+j-(start+length+1)+1;
}
else
{
copy[indexcopy--]=data[j--];
}
}
for(;i>=start;i--)
copy[indexcopy--]=data[i];
for(;j>=start+length+1;j--)
copy[indexcopy--]=data[j];
return left+right+count;
}
};