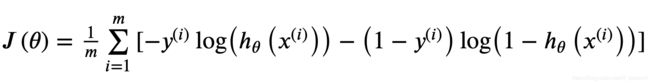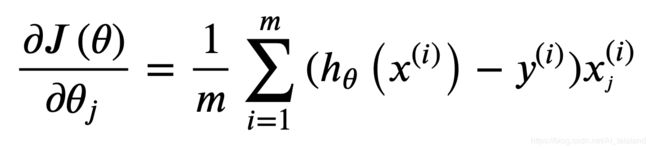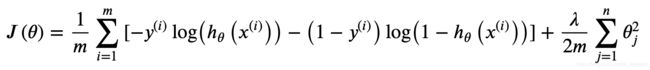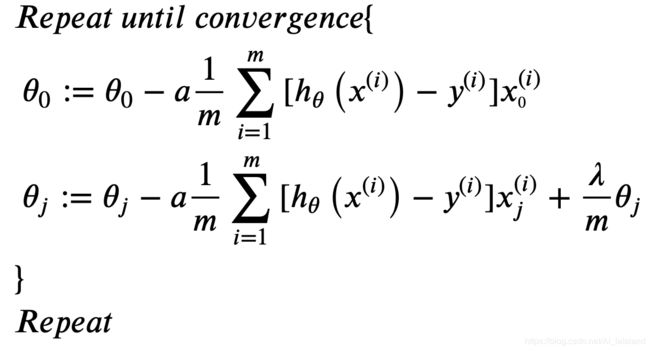吴恩达机器学习CS229A_EX2_逻辑回归与正则化_Python3
逻辑回归
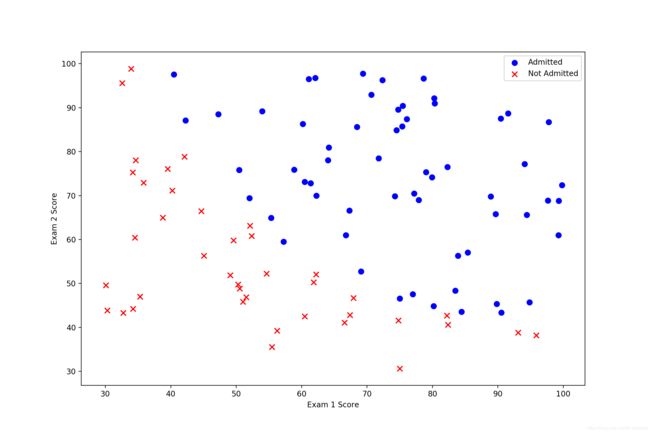
问题描述:特征集为学生的两门课的成绩,标签集为是否被大学录取。
说明:
- 这里调用 scipy 库函数执行梯度下降的具体迭代,不用手动设置步长和迭代次数,但 cost 如何计算、梯度如何求取需要以函数形式传递给 scipy;
- numpy 对 array 执行矩阵运算时,对数据格式比较严格,程序中调用了好几次 shape() 用于将形如 (100, ) 的数据格式转化为 (100, 1),这样执行矩阵乘法才能得到正确结果。
首先导入并可视化数据:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.optimize as opt
def loadData(filename):
return pd.read_csv(filename, header = None, names = ['Exam 1', 'Exam 2', 'Admitted'])
def showData(data):
positive = data[data['Admitted'].isin([1])]
negative = data[data['Admitted'].isin([0])]
fig, ax = plt.subplots(figsize = (12, 8))
ax.scatter(positive['Exam 1'], positive['Exam 2'], s=50, c='b', marker='o', label='Admitted')
ax.scatter(negative['Exam 1'], negative['Exam 2'], s=50, c='r', marker='x', label='Not Admitted')
ax.legend()
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
plt.show()
data = loadData('ex2data1.txt')
print(data.head())
print(data.describe())
showData(data) Exam 1 Exam 2 Admitted
0 34.623660 78.024693 0
1 30.286711 43.894998 0
2 35.847409 72.902198 0
3 60.182599 86.308552 1
4 79.032736 75.344376 1
Exam 1 Exam 2 Admitted
count 100.000000 100.000000 100.000000
mean 65.644274 66.221998 0.600000
std 19.458222 18.582783 0.492366
min 30.058822 30.603263 0.000000
25% 50.919511 48.179205 0.000000
50% 67.032988 67.682381 1.000000
75% 80.212529 79.360605 1.000000
max 99.827858 98.869436 1.000000
Process finished with exit code 0接着对数据预处理(这里将 X,y,theta 都转化为 numpy 的 array 格式):
def initData(data):
data.insert(0, 'Ones', 1)
cols = data.shape[1]
X = data.iloc[:, 0: cols - 1]
y = data.iloc[:, cols - 1: cols]
X = np.array(X.values)
y = np.array(y.values)
theta = np.zeros(3)
return X, y, thetadata = loadData('ex2data1.txt')
X, y, theta = initData(data)
print(X.shape, theta.shape, y.shape)(100, 3) (3,) (100, 1)
Process finished with exit code 0根据如下公式计算 cost:
# 辅助函数:计算 sigmoid
def sigmoid(z):
return 1 / (1 + np.exp(-z))
# 计算 cost
def cost(theta, X, y):
# theta 参数个数
n = len(theta)
first = -y * np.log(sigmoid(X @ theta.reshape(n, 1)))
second = -(1 - y) * np.log(1 - sigmoid(X @ theta.reshape(n, 1)))
return np.sum(first + second) / (len(X))根据如下公式进行梯度下降:
# 计算单次梯度下降
def gradient(theta, X, y):
# theta 参数个数
n = len(theta)
# 样本数
m = len(y)
grad = np.zeros(n)
error = sigmoid(X @ theta.reshape(n, 1)) - y
for i in range(n):
term = error * X[:, i].reshape(m, 1)
grad[i] = np.sum(term) / m
return grad调用 scipy 使用 TNC 寻找最优参数:
data = loadData('ex2data1.txt')
X, y, theta = initData(data)
# 利用 SciPy 的 truncated newton(TNC) 寻找最优参数
result = opt.fmin_tnc(func=cost, x0=theta, fprime=gradient, args=(X, y))
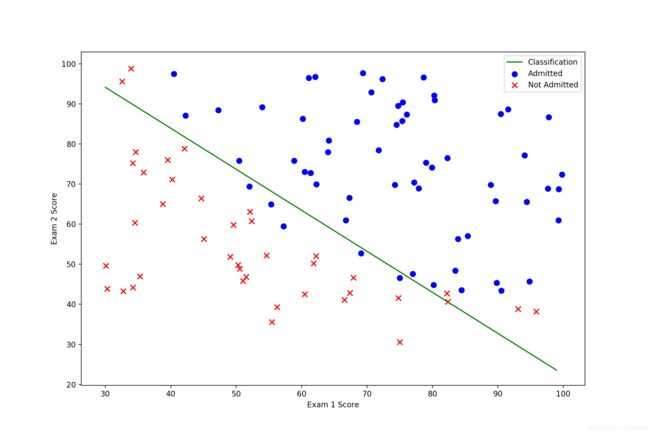
print(result)(array([-25.16131866, 0.20623159, 0.20147149]), 36, 0)绘图:
def showClassification(result, data):
x = np.arange(30, 100, step=1)
f = (- result[0][0] - x * result[0][1]) / result[0][2]
positive = data[data['Admitted'].isin([1])]
negative = data[data['Admitted'].isin([0])]
fig, ax = plt.subplots(figsize=(12, 8))
ax.scatter(positive['Exam 1'], positive['Exam 2'], s=50, c='b', marker='o', label='Admitted')
ax.scatter(negative['Exam 1'], negative['Exam 2'], s=50, c='r', marker='x', label='Not Admitted')
ax.plot(x, f, 'g', label='Classification')
ax.legend()
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
plt.show()统计训练集数据分类的正确率:
def predict(theta, X):
n = len(theta)
probability = sigmoid(X @ theta.reshape(n, 1))
return [1 if x >= 0.5 else 0 for x in probability]
data = loadData('ex2data1.txt')
X, y, theta = initData(data)
# 利用 SciPy 的 truncated newton(TNC) 寻找最优参数
result = opt.fmin_tnc(func=cost, x0=theta, fprime=gradient, args=(X, y))
print(result)
theta_get = np.array(result[0])
predictions = predict(theta_get, X)
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)]
accuracy = (sum(correct) / len(correct)) * 100
print ('accuracy = {0}%'.format(accuracy))(array([-25.16131866, 0.20623159, 0.20147149]), 36, 0)
accuracy = 89%
Process finished with exit code 0完整的逻辑回归程序:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.optimize as opt
def loadData(filename):
return pd.read_csv(filename, header = None, names = ['Exam 1', 'Exam 2', 'Admitted'])
def showData(data):
positive = data[data['Admitted'].isin([1])]
negative = data[data['Admitted'].isin([0])]
fig, ax = plt.subplots(figsize = (12, 8))
ax.scatter(positive['Exam 1'], positive['Exam 2'], s=50, c='b', marker='o', label='Admitted')
ax.scatter(negative['Exam 1'], negative['Exam 2'], s=50, c='r', marker='x', label='Not Admitted')
ax.legend()
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
plt.show()
def initData(data):
data.insert(0, 'Ones', 1)
cols = data.shape[1]
X = data.iloc[:, 0: cols - 1]
y = data.iloc[:, cols - 1: cols]
X = np.array(X.values)
y = np.array(y.values)
theta = np.zeros(3)
return X, y, theta
# 辅助函数:计算 sigmoid
def sigmoid(z):
return 1 / (1 + np.exp(-z))
# 计算 cost
def cost(theta, X, y):
# theta 参数个数
n = len(theta)
first = -y * np.log(sigmoid(X @ theta.reshape(n, 1)))
second = -(1 - y) * np.log(1 - sigmoid(X @ theta.reshape(n, 1)))
return np.sum(first + second) / (len(X))
# 计算单次梯度下降
def gradient(theta, X, y):
# theta 参数个数
n = len(theta)
# 样本数
m = len(y)
grad = np.zeros(n)
error = sigmoid(X @ theta.reshape(n, 1)) - y
for i in range(n):
term = error * X[:, i].reshape(m, 1)
grad[i] = np.sum(term) / m
return grad
def showClassification(result, data):
x = np.arange(30, 100, step=1)
f = (- result[0][0] - x * result[0][1]) / result[0][2]
positive = data[data['Admitted'].isin([1])]
negative = data[data['Admitted'].isin([0])]
fig, ax = plt.subplots(figsize=(12, 8))
ax.scatter(positive['Exam 1'], positive['Exam 2'], s=50, c='b', marker='o', label='Admitted')
ax.scatter(negative['Exam 1'], negative['Exam 2'], s=50, c='r', marker='x', label='Not Admitted')
ax.plot(x, f, 'g', label='Classification')
ax.legend()
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
plt.show()
def predict(theta, X):
n = len(theta)
probability = sigmoid(X @ theta.reshape(n, 1))
return [1 if x >= 0.5 else 0 for x in probability]
data = loadData('ex2data1.txt')
#showData(data)
X, y, theta = initData(data)
# 利用 SciPy 的 truncated newton(TNC) 寻找最优参数
result = opt.fmin_tnc(func=cost, x0=theta, fprime=gradient, args=(X, y))
print(result)
#showClassification(result, data)
theta_get = np.array(result[0])
predictions = predict(theta_get, X)
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)]
accuracy = (sum(map(int, correct)) % len(correct))
print ('accuracy = {0}%'.format(accuracy))
正则化逻辑回归
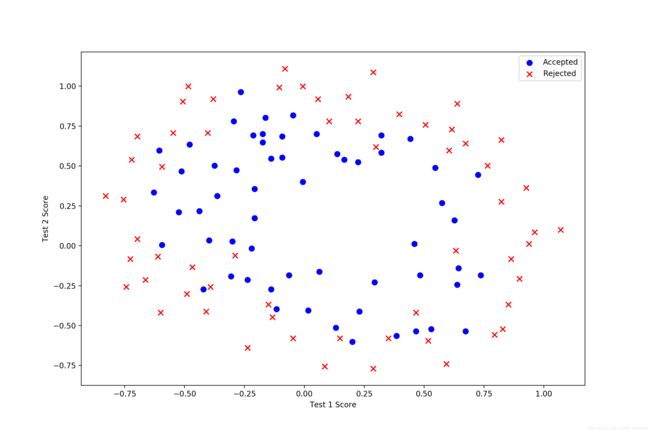
问题描述:特征集是芯片两次测试的数据,标签集是芯片是否丢弃,要求用正则化的逻辑回归进行分类。
说明:
- 以逻辑回归的程序为基础,改写计算 cost 和梯度的函数,下面可以看到公式,非常直观;
- 主要改动在于数据的初始化,使用多项式方法提取特征,这里值得注意一下;
- 其他相似的代码只在最后完整程序贴出。
首先读取并可视化数据:
初始化数据集,用多项式方法提取特征:
# degree:多项式回归允许的最大次方数
def initData(data, degree = 5):
# 特征集数量
parameters = int((degree + 1) * (degree + 2) / 2)
# 在 data 中添加多项式项
x1 = data['Test 1']
x2 = data['Test 2']
for i in range(0, degree + 1):
for j in range(0, degree + 1 - i):
data['F' + str(i) + str(j)] = np.power(x1, i) * np.power(x2, j)
# 生成 X、y、theta 的 array 数据
cols = data.shape[1]
X = data.iloc[:, 3: cols]
y = data.iloc[:, 2: 3]
X = np.array(X.values)
y = np.array(y.values)
theta = np.zeros(parameters)
return X, y, thetadata = loadData('ex2data2.txt')
X, y, theta = initData(data)
print(data.head())
print(X.shape, theta.shape, y.shape) Test 1 Test 2 Accepted F00 ... F32 F40 F41 F50
0 0.051267 0.69956 1 1.0 ... 0.000066 0.000007 0.000005 3.541519e-07
1 -0.092742 0.68494 1 1.0 ... -0.000374 0.000074 0.000051 -6.860919e-06
2 -0.213710 0.69225 1 1.0 ... -0.004677 0.002086 0.001444 -4.457837e-04
3 -0.375000 0.50219 1 1.0 ... -0.013299 0.019775 0.009931 -7.415771e-03
4 -0.513250 0.46564 1 1.0 ... -0.029315 0.069393 0.032312 -3.561597e-02
[5 rows x 24 columns]
(118, 21) (21,) (118, 1)
Process finished with exit code 0根据如下公式改写 cost 计算方法:
# 计算 cost
def costReg(theta, X, y, lamda):
# theta 参数个数
n = len(theta)
# 样本数
m = len(y)
first = -y * np.log(sigmoid(X @ theta.reshape(n, 1)))
second = -(1 - y) * np.log(1 - sigmoid(X @ theta.reshape(n, 1)))
reg = (lamda / (2 * m)) * np.sum(np.power(theta.reshape(n, 1), 2))
return (np.sum(first + second) / m) + reg根据如下公式改写梯度计算方法:
# 计算单次梯度下降
def gradientReg(theta, X, y, lamda):
# theta 参数个数
n = len(theta)
# 样本数
m = len(y)
grad = np.zeros(n)
error = sigmoid(X @ theta.reshape(n, 1)) - y
for i in range(n):
term = error * X[:, i].reshape(m, 1)
if(i == 0):
grad[i] = np.sum(term) / m
else:
grad[i] = (np.sum(term) / len(X)) + ((lamda / len(X)) * theta.reshape(n, 1)[i])
return grad运行并测试(可以尝试增加 lamda,正确率会下降,但是泛化能力可能会提高):
lamda = 1
data = loadData('ex2data2.txt')
X, y, theta = initData(data)
# 利用 SciPy 的 truncated newton(TNC) 寻找最优参数
result = opt.fmin_tnc(func=costReg, x0=theta, fprime=gradientReg, args=(X, y, lamda))
print(result)
theta_get = np.array(result[0])
predictions = predict(theta_get, X)
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)]
accuracy = (sum(correct) / len(correct)) * 100
print ('accuracy = {0}%'.format(accuracy))(array([ 1.25428442, 1.19474489, -1.49491004, -0.29714827, -1.39749019,
-0.67605408, 0.61391241, -0.89234232, -0.36100897, -0.25106153,
-0.28291693, -2.1579572 , -0.36841775, -0.62674956, -0.27932149,
0.0560712 , -0.07305438, -0.06419001, -1.62631552, -0.22204016,
-0.32974837]), 54, 4)
accuracy = 83.89830508474576%
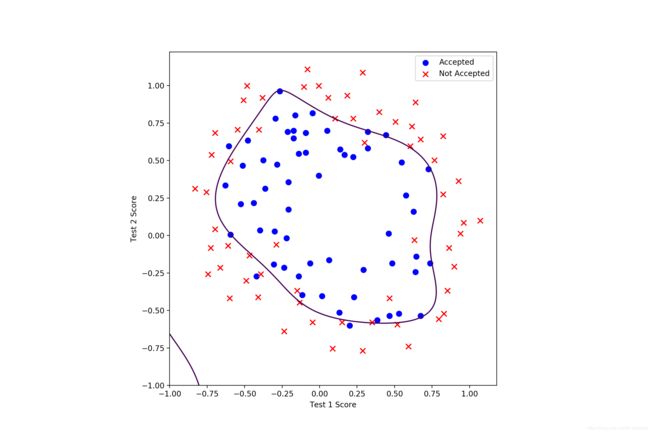
Process finished with exit code 0绘图(多项数最大阶数取 5)
这里可应该有更简洁的方式绘制多项式曲线,笔者就用 matplotlib 的 contour 来做了。
def showClassificationReg(result, data):
x = y = np.arange(-1, 1, 0.01)
x, y = np.meshgrid(x, y)
positive = data[data['Accepted'].isin([1])]
negative = data[data['Accepted'].isin([0])]
fig, ax = plt.subplots(figsize=(12, 8))
ax.scatter(positive['Test 1'], positive['Test 2'], s=50, c='b', marker='o', label='Accepted')
ax.scatter(negative['Test 1'], negative['Test 2'], s=50, c='r', marker='x', label='Not Accepted')
plt.contour(x, y, result[0][1]*y + result[0][2]*(y**2) + result[0][3]*(y**3) + result[0][4]*(y**4) + result[0][5]*(y**5)\
+ result[0][6]*x + result[0][7]*x*y + result[0][8]*x*(y**2) + result[0][9]*x*(y**3) + result[0][10]*x*(y**4)\
+ result[0][11]*(x**2) + result[0][12]*(x**2)*y + result[0][13]*(x**2)*(y**2) + result[0][14]*(x**2)*(y**3)\
+ result[0][15]*(x**3) + result[0][16]*(x**3)*y + result[0][17]*(x**3)*(y**2)\
+ result[0][18]*(x**4) + result[0][19]*(x**4)*y + result[0][20]*(x**5), [-result[0][0]])
plt.axis('scaled')
ax.legend()
ax.set_xlabel('Test 1 Score')
ax.set_ylabel('Test 2 Score')
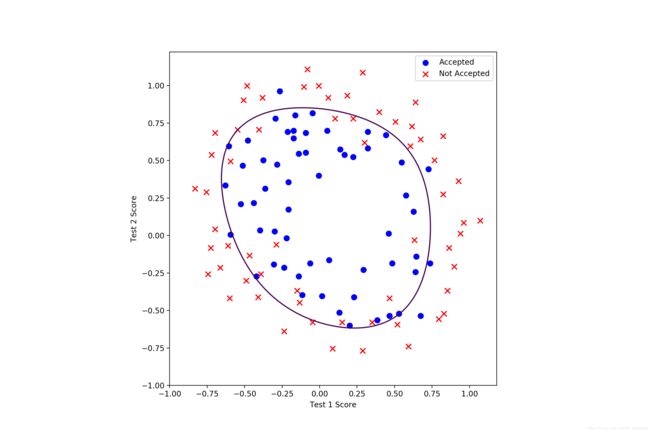
plt.show()lamda = 0(训练集正确率 88.98305084745762%):过拟合(若最大阶数更高,得到的曲线会更加扭曲)
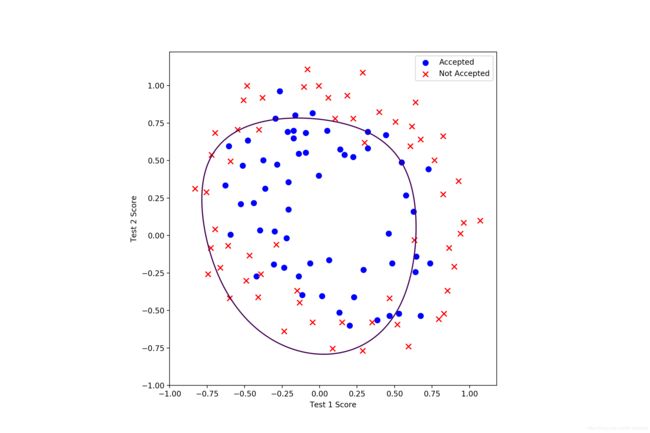
lamda = 1(训练集正确率 83.89830508474576%):结果较好
lamda = 10(训练集正确率 70.33898305084746%):欠拟合
完整的正则化逻辑回归程序:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.optimize as opt
def loadData(filename):
return pd.read_csv(filename, header = None, names = ['Test 1', 'Test 2', 'Accepted'])
def showData(data):
positive = data[data['Accepted'].isin([1])]
negative = data[data['Accepted'].isin([0])]
fig, ax = plt.subplots(figsize = (12, 8))
ax.scatter(positive['Test 1'], positive['Test 2'], s=50, c='b', marker='o', label='Accepted')
ax.scatter(negative['Test 1'], negative['Test 2'], s=50, c='r', marker='x', label='Rejected')
ax.legend()
ax.set_xlabel('Test 1 Score')
ax.set_ylabel('Test 2 Score')
plt.show()
# degree:多项式回归允许的最大阶数
def initData(data, degree = 5):
# 特征集数量
parameters = int((degree + 1) * (degree + 2) / 2)
# 在 data 中添加多项式项
x1 = data['Test 1']
x2 = data['Test 2']
for i in range(0, degree + 1):
for j in range(0, degree + 1 - i):
data['F' + str(i) + str(j)] = np.power(x1, i) * np.power(x2, j)
# 生成 X、y、theta 的 array 数据
cols = data.shape[1]
X = data.iloc[:, 3: cols]
y = data.iloc[:, 2: 3]
X = np.array(X.values)
y = np.array(y.values)
theta = np.zeros(parameters)
return X, y, theta
# 辅助函数:计算 sigmoid
def sigmoid(z):
return 1 / (1 + np.exp(-z))
# 计算 cost
def costReg(theta, X, y, lamda):
# theta 参数个数
n = len(theta)
# 样本数
m = len(y)
first = -y * np.log(sigmoid(X @ theta.reshape(n, 1)))
second = -(1 - y) * np.log(1 - sigmoid(X @ theta.reshape(n, 1)))
reg = (lamda / (2 * m)) * np.sum(np.power(theta.reshape(n, 1), 2))
return (np.sum(first + second) / m) + reg
# 计算单次梯度下降
def gradientReg(theta, X, y, lamda):
# theta 参数个数
n = len(theta)
# 样本数
m = len(y)
grad = np.zeros(n)
error = sigmoid(X @ theta.reshape(n, 1)) - y
for i in range(n):
term = error * X[:, i].reshape(m, 1)
if(i == 0):
grad[i] = np.sum(term) / m
else:
grad[i] = (np.sum(term) / len(X)) + ((lamda / len(X)) * theta.reshape(n, 1)[i])
return grad
def predict(theta, X):
n = len(theta)
probability = sigmoid(X @ theta.reshape(n, 1))
return [1 if x >= 0.5 else 0 for x in probability]
def showClassificationReg(result, data):
x = y = np.arange(-1, 1, 0.01)
x, y = np.meshgrid(x, y)
positive = data[data['Accepted'].isin([1])]
negative = data[data['Accepted'].isin([0])]
fig, ax = plt.subplots(figsize=(12, 8))
ax.scatter(positive['Test 1'], positive['Test 2'], s=50, c='b', marker='o', label='Accepted')
ax.scatter(negative['Test 1'], negative['Test 2'], s=50, c='r', marker='x', label='Not Accepted')
plt.contour(x, y, result[0][1]*y + result[0][2]*(y**2) + result[0][3]*(y**3) + result[0][4]*(y**4) + result[0][5]*(y**5)\
+ result[0][6]*x + result[0][7]*x*y + result[0][8]*x*(y**2) + result[0][9]*x*(y**3) + result[0][10]*x*(y**4)\
+ result[0][11]*(x**2) + result[0][12]*(x**2)*y + result[0][13]*(x**2)*(y**2) + result[0][14]*(x**2)*(y**3)\
+ result[0][15]*(x**3) + result[0][16]*(x**3)*y + result[0][17]*(x**3)*(y**2)\
+ result[0][18]*(x**4) + result[0][19]*(x**4)*y + result[0][20]*(x**5), [-result[0][0]])
plt.axis('scaled')
ax.legend()
ax.set_xlabel('Test 1 Score')
ax.set_ylabel('Test 2 Score')
plt.show()
lamda = 1
data = loadData('ex2data2.txt')
#showData(data)
X, y, theta = initData(data)
# 利用 SciPy 的 truncated newton(TNC) 寻找最优参数
result = opt.fmin_tnc(func=costReg, x0=theta, fprime=gradientReg, args=(X, y, lamda))
print(result)
showClassificationReg(result, data)
theta_get = np.array(result[0])
predictions = predict(theta_get, X)
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)]
accuracy = (sum(correct) / len(correct)) * 100
print ('accuracy = {0}%'.format(accuracy))