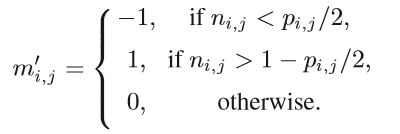深度学习在信息隐藏中的应用(下)
上一篇主要是使用卷积神经网络来做隐写分析,这一篇主要介绍几篇使用生成对抗网络来做隐写和加密。在介绍这些工作之前,我们先来看一下什么是生成对抗网络。
生成对抗网络(Generative Adversarial Network, GAN)是深度学习中一个新的网络结构,其自2014年被提出以来一直备受关注,不断有新的GAN模型或基于GAN的应用出现。GAN提出了一种不需要大量标注训练数据就能学习深度表征的方法,其采用一个极大极小博弈(minmax game)来训练得到一个生成器和判别器。在图像领域中,现有数据集中的图像可能服从一个分布 p d a t a ( x ) p_{data}(x) pdata(x),生成器G尝试去生成图像,使得生成的图像分布越来越接近真实图像的分布(这也就让生成图像看起来越来像真实图像);而判别器D则尽可能地区分出真实图像(real image)和生成的图像(fake image)。下面是一个GAN的示意图。
GAN的训练目标是获得令判别器分类准确率最大化的参数,以及获得最大化欺骗判别器的生成器参数。训练的代价由一个价值函数V(G, D)来评估,其中包含了生成器和判别器的参数,下面是这个价值函数。
min G max D V ( D , G ) = E x ∼ p d a t a ( x ) l o g ( D ( x ) ) + E z ∼ p n o i s e ( z ) l o g ( 1 − D ( G ( z ) ) ) \min\limits_{G}\max\limits_{D}V(D,G)=E_{x\sim p_{data}(x)}log(D(x))+E_{z\sim p_{noise}(z)}log(1-D(G(z))) GminDmaxV(D,G)=Ex∼pdata(x)log(D(x))+Ez∼pnoise(z)log(1−D(G(z)))
为了优化这个最小最大化问题,在使用mini-batch随机梯度进行每一次迭代时,算法分别计算V(G, D)对生成器G的参数 W G W_G WG和对判别器D的参数 W D W_D WD的梯度。在更新参数时,对于生成器G来说,我们的目标是最小化价值函数,因此有
W G ← W G − γ G ∇ G V W_G\leftarrow W_G-\gamma_G\nabla_GV WG←WG−γG∇GV
其中,
∇ G V = ∂ ∂ W G E z ∼ p n o i s e ( z ) l o g ( 1 − D ( G ( z , W G ) , W D ) ) \nabla_GV=\frac{\partial}{\partial W_G}E_{z\sim p_{noise}(z)}log(1-D(G(z, W_G), W_D)) ∇GV=∂WG∂Ez∼pnoise(z)log(1−D(G(z,WG),WD))
对于生成器D来说,我们的目标则是要最大化价值函数,因此有
W D ← W D + γ D ∇ D V W_D\leftarrow W_D+\gamma_D\nabla_DV WD←WD+γD∇DV
其中,
∇ D V = ∂ ∂ W D { E x ∼ p d a t a ( x ) l o g ( D ( x , W D ) ) + E z ∼ p n o i s e ( z ) l o g ( 1 − D ( G ( z , W G ) , W D ) ) } \nabla_DV=\frac{\partial}{\partial W_D}\{E_{x\sim p_{data}(x)}log(D(x,W_D))+E_{z\sim p_{noise}(z)}log(1-D(G(z,W_G),W_D))\} ∇DV=∂WD∂{Ex∼pdata(x)log(D(x,WD))+Ez∼pnoise(z)log(1−D(G(z,WG),WD))}
最终训练的效果就是生成器G生成的图像的分布很接近真实图像的分布,判别器已经不能分清真假。下图是使用GAN去生成手写数字时前40个epoch的训练过程的一个可视化,可以看到开始的时候生成器的输出就是一些噪声,随着训练的进行生成图像慢慢显现出了手写数字的样子,且越来越真实。
Learning to Protect Communications with Adversarial Neural Cryptography
这是Google Brain的一篇,应该也是最早将深度学习应用于加密的工作了。考虑一个对称加密体制:Alice和Bob想要安全地进行通信,Eve监听了信道但不能发起会话、注入消息或者在传输中修改消息。整个场景如图2-3所示:Alice将明文P和密钥K加密产生密文C,然后将C放到信道上进行传输。Bob使用密钥K从接受到的密文C恢复出明文 P B o b P_{Bob} PBob,而监听者Eve在没有密钥K的情况下尝试从密文C中恢复出明文 P E v e P_{Eve} PEve。
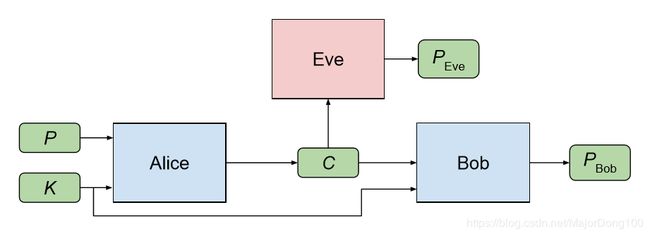
在这里,Alice,Bob,Eve三者都是卷积神经网络,它们的参数分别为 θ A \theta_{A} θA, θ B \theta_{B} θB和 θ E \theta_{E} θE。加密模型和解密模型,即Alice和Bob有着相同的网络结构,但参数不同。对于大多数神经网络来说,模型的输入和输出通常都是浮点数,而不是比特序列,因此这里的P,K, P B o b P_{Bob} PBob和 P E v e P_{Eve} PEve都可能是浮点数。即是P和K是0和1组成的比特序列,C、 P B o b P_{Bob} PBob和 P E v e P_{Eve} PEve也可以是任意的浮点数。在实际操作中,我们将它们限制在区间(-1, 1)内。
Eve的目标很简单,即能够准确地从窃听到的密文C中恢复出明文P,也就是尽可能地缩小P和 P E v e P_{Eve} PEve之间的误差。Alice和Bob呢,则希望能够安全准确地进行通信,换句话说就是尽可能地缩小P和 P B o b P_{Bob} PBob之间的误差。根据现代密码学的定义,我们不必要求密文C对Eve来说一定要是随机的(look random),因此从随机数中分辨出密文C不是Eve的目标。
因此,整个生成对抗网络包含三个部分,下表说明了三个部分的输入输出。
| Model | Input | Output |
|---|---|---|
| Alice | P, K | A ( θ A , P , K ) A(\theta_{A}, P, K) A(θA,P,K) |
| Bob | C, K | B ( θ B , C , K ) B(\theta_{B}, C, K) B(θB,C,K) |
| Eve | C | E ( θ E , C ) E(\theta_{E}, C) E(θE,C) |
我们引入明文之间的距离函数d,这里使用L1距离: d ( P , P ′ ) = ∑ i = 1 N ∣ P i − P i ′ ∣ d(P, P^{'})=\sum_{i=1}^{N}|P_i-P^{'}_i| d(P,P′)=∑i=1N∣Pi−Pi′∣,其中N为明文长度。因此对于每一个样本,Eve的损失函数为:
L E ( θ A , θ E , P , K ) = d ( P , E ( θ E , A ( θ A , P , K ) ) ) L_E(\theta_A, \theta_E, P, K)=d(P, E(\theta_E, A(\theta_A, P, K))) LE(θA,θE,P,K)=d(P,E(θE,A(θA,P,K)))
那么,Eve在明文P和密钥K的分布下的损失函数为:
L E ( θ A , θ E ) = E P , K ( d ( P , E ( θ E , A ( θ A , P , K ) ) ) ) L_E(\theta_A, \theta_E)=E_{P, K}(d(P, E(\theta_E, A(\theta_A, P, K)))) LE(θA,θE)=EP,K(d(P,E(θE,A(θA,P,K))))
Eve的目标也就如下:
O E ( θ A ) = a r g m i n θ E ( L E ( θ A , θ E ) ) O_E(\theta_A)=argmin_{\theta_E}(L_E(\theta_A, \theta_E)) OE(θA)=argminθE(LE(θA,θE))
类似的,Bob针对某个样本的损失函数和在明文P和密钥K的分布下的损失函数分别如下:
L B ( θ A , θ B , P , K ) = d ( P , B ( θ B , A ( θ A , P , K ) , K ) ) L_B(\theta_A, \theta_B, P, K)=d(P, B(\theta_B, A(\theta_A, P, K), K)) LB(θA,θB,P,K)=d(P,B(θB,A(θA,P,K),K))
L B ( θ A , θ B ) = E P , K ( d ( P , B ( θ B , A ( θ A , P , K ) , K ) ) ) L_B(\theta_A, \theta_B)=E_{P, K}(d(P, B(\theta_B, A(\theta_A, P, K), K))) LB(θA,θB)=EP,K(d(P,B(θB,A(θA,P,K),K)))
综上,对于Alice和Bob来说,损失函数如下:
L A B ( θ A , θ B ) = L B ( θ A , θ B ) − L E ( θ A , O E ( θ A ) ) L_{AB}(\theta_A, \theta_B)=L_B(\theta_A, \theta_B)-L_E(\theta_A, O_E(\theta_A)) LAB(θA,θB)=LB(θA,θB)−LE(θA,OE(θA))
限定明文和密钥长度相等,Alice和Bob的模型结构相同,如图2-2所示(图是用keras画的,图中取明文长度N为64)。Eve则将前两层改成N-2N的全连接,其余一样。
图2-5为N=16时的最后的训练结果。后面论文还讨论了如何去学习加密,我没仔细看。

Steganographic generative adversarial networks
这篇论文连续投了2016年和2017年的ICLR(International Conference on Learning Representations,这个会议是由深度学习三大巨头之二的Yoshua Bengio和Yann LeCun两个人牵头举办的,现在已经成为了深度学习领域的顶会),好像都没有中。这篇是我看到的第一篇将生成对抗网络应用到信息隐藏领域的文章,下面对其进行一个概述。
这篇文章在DCGAN(Deep Convolutional Generative Adversarial Networks)的基础上提出了SGAN(Steganographic Generative Adversarial Networks),它主要是在经典GAN的基础上加了一个由CNN实现的判别器网络S对输入给S的图像进行隐写分析,模型示意图如下图所示。输入给S的图像一部分通过一个传统隐写算法做了隐写,另外一部分没有。

因为模型里加了隐写分析器S,所以用来衡量模型的价值函数就变成了下面这个样子,其中的 α \alpha α是一个超参数。
min G max D max S V ( D , G , S ) = α V ( D , G ) + ( 1 − α ) V ( G , S ) \min\limits_{G}\max\limits_{D}\max\limits_{S}V(D,G,S)=\alpha V(D,G)+(1-\alpha)V(G,S) GminDmaxSmaxV(D,G,S)=αV(D,G)+(1−α)V(G,S)
其中,
E z ∼ p n o i s e ( z ) [ l o g S ( S t e g o ( G ( z ) ) ) + l o g ( 1 − S ( G ( z ) ) ) ] E_{z\sim p_{noise}(z)}[logS(Stego(G(z)))+log(1-S(G(z)))] Ez∼pnoise(z)[logS(Stego(G(z)))+log(1−S(G(z)))]
训练方法同经典GAN一样,采用mini-batch的随机梯度法,迭代式地分别训练三个网络,具体的参数更新函数这里就不再赘述了,基本跟前面的一样。
论文使用了名人集作为数据集,其中包含了200000张名人照片,全剪切成了64x64的大小。其中的10%的数据做为测试集,其他作为训练集。这里使用的隐写算法是正负一嵌入算法,也就是LSB,嵌入率为0.4,且只在图像的一个通道内嵌入秘密信息。
我们用C2D-BN-LR来表示这样的一块(block)网络结构:Conv2D-Batch Normalization-Leaky ReLU。判别器D和隐写分析器S使用了相似的网络结构:四块C2D-BN-LR后面跟的直接就是一个sigmoid单元。生成器G按顺序先是一个含有8192的单元的全连接层,然后后边是4块C2D-BN-LR(里边使用的是反卷积),最后跟着一个tanh函数用来输出归一化的结果。训练过程使用了Adam作为优化器,学习率为 2 − 4 2^{-4} 2−4,更新参数分别取 β 1 = 0.5 \beta_1=0.5 β1=0.5和 β 2 = 0.999 \beta_2=0.999 β2=0.999。在每一个mini-batch上训练时,每更新D和S的参数一次就更新G的参数两次。
另外,还设计了一个独立的隐写分析器 S ∗ S^* S∗,该模型结构为Conv2D-Conv2D-Conv2D-Max Pooling-Conv2D-Conv2D-Max Pooling-Fully connected layer,其中第一层卷积使用的卷积核就是上篇中Qian等使用的卷积核。
最后的结果是使用DCGAN生成的图像比自然图像更适合做隐写载体。
SSGAN: secure steganography based on generative adversarial networks
这篇paper是上篇博客中中科院的后续工作,是在上篇之后出来的,它的主要工作有以下三点:
1.使用WGAN替代上篇中的DCGAN,生成图像的可视化质量更高,训练速度也更快;
2.使用上篇博客中的GNCNN替代上篇中的隐写分析器;
3.使用GNCNN和GAN进行对抗,使GAN生成的图像更适合隐写。
最后的结果是用WGAN生成的图像比用DCGAN生成的图像更适合做隐写,比DCGAN训练速度更快。
Automatic steganographic distortion learning using a generative adversarial network
这篇文章是首次使用GAN来做隐写,去搜索一张图像中的隐写位置,设计一个自己的框架ASDL-GAN。
一个成功的隐写算法要尽可能地减小cover和stego之间的差距,X和Y分别代表cover和stego, x i , j x_{i,j} xi,j和 y i , j y_{i,j} yi,j分别表示其中的像素点,因此就有了一个失真函数:
D ( X , Y ) = ∑ i = 1 H ∑ j = 1 W ρ i , j ∣ x i , j − y i , j ∣ D(X, Y)=\sum_{i=1}^{H}\sum_{j=1}^{W}\rho_{i,j}|x_{i,j}-y_{i,j}| D(X,Y)=i=1∑Hj=1∑Wρi,j∣xi,j−yi,j∣
H和W分别是图像的高和宽, ρ i , j \rho_{i,j} ρi,j表示像素 x i , j x_{i,j} xi,j和 y i , j y_{i,j} yi,j之间的改变对应的一个代价值。 ρ \rho ρ是由现有的内容自适应空域隐写算法如HUGO、S-UNIWARD和HILL等设计的。给定嵌入率和嵌入代价矩阵,由每个像素改变可能性组成的改变矩阵 P = ( p i , j ) H ∗ W P=(p_{i,j})^{H*W} P=(pi,j)H∗W也就确定了。
上面是传统的隐写算法中使用的方法,这里我们反过来:我们首先通过模型学习到图像的改变矩阵P,然后根据这个改变矩阵来得出代价矩阵 ρ \rho ρ。
ρ i , j = l n ( 1 / p i , j − 2 ) \rho_{i,j}=ln(1/p_{i,j}-2) ρi,j=ln(1/pi,j−2)
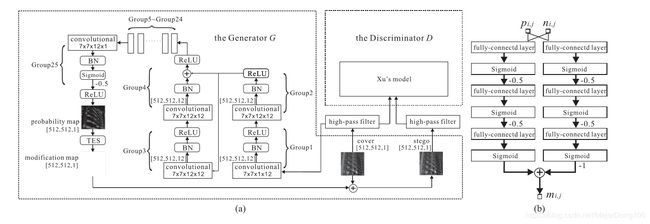
因此,在这个模型中,生成器G用来学习一个输入图像的改变矩阵P,判别器D则试图分辨出经G产生的改变矩阵隐写过的stego。生成器G的结构下面会细讲,判别器D的结构采用了上篇博客介绍的Xu等的模型。为了根据G生成的改变矩阵去做隐写生成stego,论文中设计了一个叫TES(ternary embedding simulator)的激活函数来模拟秘密信息的嵌入过程,这个激活函数是通过一个小的神经网络实现的,后面会详细介绍。
生成器G的结构分成了25个group,前24个group的结构都一样,先是一个卷积尺寸为7x7的卷积层,后边是Batch Normalization,最后是ReLU激活函数。第偶数个group的输出会同时输入给下面的两个group。最后一个group的输出只有一个feature map,所有值都在(0, 1)之间。更进一步地,输出矩阵在全部减去一个0.5之后又经过了一个ReLU激活函数来确保最终的输出全在(0, 0.5)之间。改变概率在(0, 0.5)之间而不是在(0, 1)之间的原因在于,改变大的改变概率对应的像素值会留下潜在的安全漏洞。另外,传统的隐写算法得出的改变矩阵也都在(0, 0.5)之间。生成器G的模型示意图如下图中a所示。
论文采取了一个三元的嵌入模式,即对于一个像素值 x i , j x_{i,j} xi,j,其改变量有三种可能:-1,1,0,其对应的由G学习到的改变概率为 p i , j p_{i,j} pi,j,则有 p i , j + 1 = p i , j − 1 = p i , j / 2 p_{i,j}^{+1}=p_{i,j}^{-1}=p_{i,j}/2 pi,j+1=pi,j−1=pi,j/2, p i , j 0 = 1 − p i , j p_{i,j}^0=1-p_{i,j} pi,j0=1−pi,j。这样以来,该图像的嵌入率也就有了:
c a p a c i t y = ∑ i = 1 H ∑ j = 1 W ( − p i , j + 1 l o g 2 p i , j + 1 − p i , j − 1 l o g 2 p i , j − 1 − p i , j 0 l o g 2 p i , j 0 ) capacity=\sum_{i=1}^{H}\sum_{j=1}^{W}(-p_{i,j}^{+1}log_2p_{i,j}^{+1}-p_{i,j}^{-1}log_2p_{i,j}^{-1}-p^0_{i,j}log_2p_{i,j}^0) capacity=i=1∑Hj=1∑W(−pi,j+1log2pi,j+1−pi,j−1log2pi,j−1−pi,j0log2pi,j0)
将生成器G的输出P输入给TES就得到了modification map,用它就可以将cover隐写成stego。传统的隐写算法中,根据一个改变概率 p i , j p_{i,j} pi,j和一个区间[0,1]之间的随机数字 n i , j n_{i,j} ni,j, n i , j n_{i,j} ni,j服从一个均匀分布,然后得出相应的改变量,具体公式如下图所示。
但是到这里有一个问题,上图中的是一个阶梯函数,存在不可导的点,因此也就不能使用反向传播,因此就有了TES。将 p i , j p_{i,j} pi,j和 n i , j n_{i,j} ni,j作为输入,TES被训练以拟合上图中的函数并尽可能的给出一个相近的输出 m i , j m_{i,j} mi,j。TES的结构如图2-7中b所示,包含两个独立的四层全连接网络,每个隐藏层包含10个神经元,在经过sigmoid激活函数后减去一个0.5(输出值也就由原来的以0.5为中心变成了以0为中心);另外,右子网络在输出后会减去一个1,这样左子网络的输出可以近似成0或1,右子网络的输出可以近似成-1或0,两个子网络的输出相加做为最终的输出,这样输出值就有-1,0,1三种可能,实现了三元激活函数。
以上就是整个模型的构想及结构,下面是训练过程。TES作为一个激活函数是要提前进行预训练的,其输入 n i , j n_{i,j} ni,j和 p i , j p_{i,j} pi,j都取自区间[0, 1],独立均匀分布。TES模型中的所有参数都由符合 ( μ = 0 , σ = 1 ) (\mu=0, \sigma=1) (μ=0,σ=1)的高斯随机数进行初始化,模型的损失函数如下:
l T E S = 1 H 1 W ∑ i = 1 H ∑ j = 1 W ( m i , j − m i , j ′ ) 2 l_{TES}=\frac{1}{H}\frac{1}{W}\sum_{i=1}^{H}\sum_{j=1}^{W}(m_{i,j}-m^{'}_{i,j})^2 lTES=H1W1i=1∑Hj=1∑W(mi,j−mi,j′)2
学习率设为0.01,batch size取1000,经过10^6的迭代,TES已经能够在超过90%的概率下输出正负一。另外,在训练整个GAN的阶段,TES的参数还会参与修正。
下面是ASDL-GAN的训练过程。判别器D的损失函数如下:
l D = − ∑ i = 1 2 y i ′ l o g ( y i ) l_D=-\sum_{i=1}^{2}y^{'}_ilog(y_i) lD=−i=1∑2yi′log(yi)
生成器G的损失函数分为 l G 1 l^1_G lG1和 l G 2 l^2_G lG2两部分, l G 1 l^1_G lG1是为了和判别器D进行博弈, l G 2 l^2_G lG2则是为了确保隐写率。
l G 1 = − l D l^1_G=-l_D lG1=−lD
l G 2 = ( c a p a c i t y − H × W × q ) 2 l^2_G=(capacity-H\times W\times q)^2 lG2=(capacity−H×W×q)2
训练G和D使用的学习率不同,训练阶段使用了40000张512x512的灰度图,最终的隐写效果从下面两张图中可以看到。图2-9展示的不同的训练次数下,该模型与S-UNIWARD的比较,可以看到在180000次迭代后,该模型的抗检测效果略次于S-UNIWARD。图2-10则是对隐写位置的可视化,其中(a)是原图,(b)是S-UNIWARD隐写位置的可视化,©到(f)则是ASDL-GAN在不同的训练次数下的可视化效果,可以看到随着训练的不断进行,其隐写位置越来越像传统算法,这也说明了该模型的可行性。
以上就是GAN在隐写分析领域的相关工作,以后有新的paper的话会有更新。
附录
[1] Mart´ın Abadi, David G. Andersen. Learning to Protect Communications with Adversarial Neural Cryptography. arXiv preprint arXiv:1610.06918,2017.
[2] Denis Volkhonskiy, Ivan Nazarov, Boris Borisenko, Evgeny Burnaev. Steganographic Generative Adversarial Networks. arXiv preprint arXiv:1703.05502,2017.
[3] Haichao Shi, Jing Dong, Wei Wang, Yinlong Qian, Xiaoyu Zhang. SSGAN: Secure Steganography Based on Generative Adversarial Networks. arXiv preprint arXiv:1707.01613,2017.
[4] Tang W, Tan S, Li B, et al. Automatic steganographic distortion learning using a generative adversarial network[J]. IEEE Signal Processing Letters, 2017, PP(99):1-1.