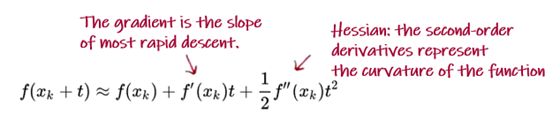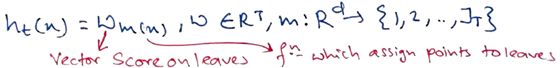XGBoost算法背后的数学:尽可能简单地解释XGBoost算法背后的机制
如果你想很好地理解某些内容,请尝试简单地给别人解释出来。 ——费曼
XGBoost是一个很优美的算法,它的过程不乏启发性。这些通常简单而美丽的概念在数学术语中消失了。我在理解数学的过程中也遇到过同样的挑战,所以我写这篇文章的目的是巩固我的理解,同时帮助其他人完成类似的过程。
为了解XGBoost是什么,我们首先要了解什么是梯度提升机Gradient Boosting,以及梯度提升机背后的数学概念。请注意,这篇文章假设你对梯度提升机非常熟悉,并试图触及梯度提升机和XGBoost背后的直觉和数学。现在我们开始吧。
理解梯度提升机
第一步 - 初始函数
与往常一样,让我们从粗略的初始函数Fo
开始,类似于回归时所有值的平均值。 它将为我们提供一些输出,无论效果如何。
第二步 - 损失函数
下面我们计算损失函数L(yi,Ft(xi))
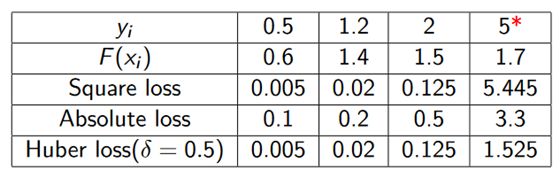
那么什么是损失函数?它是一种度量预测值与真实值之间差异的算式,这里有几个例子:
从下表可以理解为什么对异常值的鲁棒性很重要:
其思想是,损失函数的值越低,我们的预测就越准确,所以获取最佳的预测值等价为损失函数的最小化问题。
第三步 - 新的目标
到目前为止,我们已经建立了我们的初始模型,并进行了预测。接下来,我们应该在损失函数给出的残差上拟合一个新模型,但有一个微妙的转折:我们将拟合损失函数的负梯度,下面给出我们为什么这样做以及为什么它们相似的直觉:
梯度可以解释为函数的“最快增加的方向和速率”,因此负梯度告诉我们函数最小值的方向,在这种情况下为损失函数的最小值。
我们将遵循梯度下降法,逐步逼近损失函数的极小值,算法的学习速率将给出每一次更新的步长。在损失函数最小的情况下,我们的错误率也最低。
因此,我们将在损失函数的-ve梯度处建立新模型ht+1
第四步 - 累加
在-ve梯度上迭代拟合模型的过程将继续进行,直到我们达到给定的弱学习器数量的最小值或极限T为止,这称为累加。
回想一下,在Adaboost中,模型的“缺点”是由高权重数据点确定的。在梯度提升机中,“缺点”是通过梯度来识别的。
简单来说,这就是梯度提升机的工作机制。在回归和分类任务中,唯一不同的是所使用的损失函数。
XGBoost
XGBoost和梯度提升机都遵循梯度提升决策树的原理,但是XGBoost使用更加正则化的模型公式来控制拟合,这使它具有更好的性能,这就是为什么它也被称为“正则提升”技术。
牛顿法
那么什么是牛顿法呢?在随机梯度下降中,我们用更少的数据点来计算梯度更新的方向,耗时也相对更少,但如果我们想要加速更新,就需要更多的数据点。而在牛顿法中,我们用来计算梯度更新的方向的耗时更多,但是需要的计算点也更少。
需要注意的重要一点是,即使梯度提升机在解决回归问题时使用梯度下降法进行优化,在解决分类问题仍然使用牛顿方法来解决优化问题。 而XGBoost在分类和回归的情况下都使用此方法。
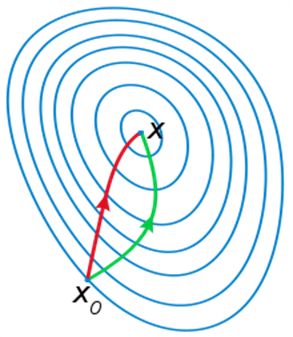
牛顿法试图通过构造一个序列{xk}来解决最小化问题,该序列从随机起点x0∈R开始,通过f的二阶泰勒展开序列收敛到f的最小值x*。f在{xk}附近的二阶泰勒展开式是
二阶导数对于加快梯度下降非常重要,因为在一个损失函数的山谷里,如果算法的修正方向是锯齿状的下降,那么您在沿着山谷的实际梯度上的进展就非常缓慢, 通过二阶导数调整方向将使您的下降方向朝山谷的实际梯度方向倾斜,从而将缓慢的下降转换为更快的下降。
损失函数
我们已经看到了平方损失函数在梯度提升机中的行为,让我们快速看一下XGBoost中平方损失函数的作用:
均方误差损失函数的形式是非常友好的,有一个一次项(通常称为剩余项)和一个二次项。对于其他值得注意的损失函数(例如logistic损失),要得到这样一个好的形式并不容易。所以在一般情况下,我们把损失函数的泰勒展开式推广到二阶
这就成了我们对新树的优化目标。该定义的一个重要优点是,目标函数的值仅依赖于pi和qi。这就是XGBoost支持自定义损失的方式。我们可以使用完全相同的以pi和qi作为输入的求解器来优化每个损失函数,包括逻辑回归和成对排序
正则化
接下来,我们将处理正则化项,但在此之前,我们需要了解如何以数学方式定义决策树。 直观来说,决策树主要是叶节点、数据点和将数据点分配给这些叶节点的函数的组合。 数学上它写为:
其中JT是叶数。此定义将树上的预测过程描述为:
- 将数据点x赋给一片叶子m
- 、将相应分数wm(x)分配给第m(x)个数据点
在XGBoost中,复杂度定义为:
XGBoost中的超参数描述如下:
当然,定义复杂度的方法不止一种,但这一种方法在实践中效果很好。正则化是大多数基于树的方法处理得不太仔细或忽略掉的一部分。这是因为传统的树学习方法只强调提升纯度,而复杂度的控制则只能基于试探。通过正式定义它,我们可以更好地了解我们的模型正在学习的内容,并获得泛化能力良好的模型
最后一个方程衡量的是树的结构的优劣。
如果听起来有些复杂,让我们看一下图片,看看如何计算分数。
基本上,对于给定的树结构,我们将统计信息gi和hi推入它们所属的叶节点,将统计信息求和,然后使用这一公式计算树的质量。 该分数类似于决策树中的纯度度量,不同之处在于它还考虑了模型的复杂性
学习树的结构
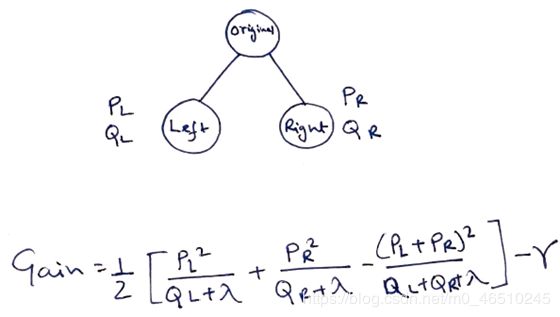
现在,我们有了一种方法来衡量一棵树的质量。理想情况下,我们将枚举所有可能的树并选择最佳的树,但实际上这是非常棘手的,因此我们将尝试一次优化一个树的部分。 具体来说,我们尝试将一片叶子分成两片叶子,其得分为
该公式可分解为: 1)新左叶上的分数;2)新右叶上的分数;3)原始叶上的分数;4)附加叶上的正则化。 我们在这里可以看到一个重要的事实:如果增益小于γ,我们最好不要添加该分支,这正是基于树的模型中的修剪技术! 通过使用监督学习的原理,我们自然可以得出这些技术起作用的原因
很好,现在希望我们对XGBoost有一个初步的了解,以及为什么它会这样工作。下次见!
作者:Dip Ranjan Chatterjee
deephub翻译组:Alexander Zhao
![]()