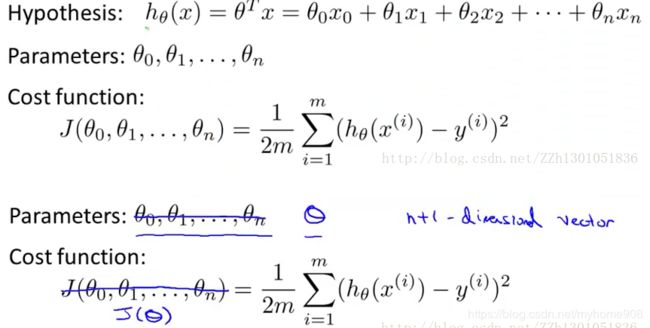梯度下降与一元线性回归python实现
线性回归
线性回归包括一元线性回归和多元线性回归。
下面是一个简单的数据集,即房屋面积和价格之间的关系,自变量是面积feet,因变量时价格price,用上述数据可以进行训练
找到一个合适的线来预测房价。
线性回归主要是进行参数 的查找,找到合适的参数使损失函数的值最小,损失函数计算公式是
真实值与预测值差的平方和。
对于上述损失函数,可以分别对西塔求偏导,采用梯度下降的方法进行循环迭代。
在进行梯度下降求解参数的时候如果已知的值过大,可以进行特征缩放或者归一化或者设置学习率来提高梯度下降的速度,
https://blog.csdn.net/ZZh1301051836/article/details/79142800
画出散点图(重新造的数据)
方法一:自己编写
import numpy as np
import matplotlib.pyplot as plt
#载入数据,用“,”分割
#data=np.getformtxt('data.csv',delimiter=',')
#取数据中所有的行,只针对第0列
#x_data=data[:,0]
x_data=np.array([6.1101, 5.5277,8.5186, 7.0032, 5.8598, 8.3829,7.476, 8.5781, 6.4862,5.0546,5.7107, 14.1640,5.7340,8.4084, 5.6407, 5.3794, 6.3654,5.1301, 6.429,7.0708, 6.1891,20.2700, 5.4901, 6.3261, 5.5649, 18.9450, 12.8280, 10.9570, 13.1760, 22.2030, 5.2524, 6.5894, 9.2482, 5.8918, 8.2111, 7.9334, 8.0959, 5.6063, 12.8360, 6.3534, 5.4069,6.8825, 11.7080,5.7737, 7.8247, 7.0931, 5.0702, 5.8014,11.7000, 5.5416,7.5402,5.3077, 7.4239,7.6031,6.3328,6.3589,6.2742, 5.6397, 9.3102, 9.4536, 8.8254, 5.1793, 21.2790, 14.9080, 18.9590, 7.2182, 8.2951, 10.2360,5.4994,20.3410,10.1360,7.3345,6.0062,7.2259,5.0269, 6.5479, 7.5386, 5.0365, 10.2740, 5.1077,5.7292,5.1884, 6.3557,9.7687, 6.5159, 8.5172,9.1802,6.0020,5.5204, 5.0594, 5.7077,7.6366, 5.8707, 5.3054, 8.2934, 13.3940, 5.4369])
#取数据中所有的行,只要第一列
#y_data=data[:,1]
y_data=np.array([ 17.5920,9.1302,13.6620,11.8540,6.8233,11.8860,4.3483,12.0000,6.5987,3.8166,3.2522,15.5050,3.1551,7.2258,0.7162,3.5129,5.3048,0.5608,3.6518,5.3893,3.1386,21.7670,4.2630,5.1875,3.0825,22.6380,13.5010,7.0467,14.6920,24.1470,-.2200,5.9966,12.1340,1.8495,6.5426,4.5623,4.1164,3.3928,10.1170,5.4974,0.5566,3.9115,5.3854,2.4406,6.7318,1.0463,5.1337,1.8440,8.0043,1.0179,6.7504,1.8396,4.2885,4.9981,1.4233,-1.4211,2.4756,4.6042,3.9624,5.4141,5.1694,-0.7428,17.929,12.0540,17.0540,4.8852,5.7442,7.7754,1.0173,20.9920,6.6799,4.0259,1.2784,3.3411,-.6807,0.2968,3.8845,5.7014,6.7526,2.0576,0.4795,0.2042,0.6786,7.5435,5.3436,4.2415,6.7981,0.9270,0.1520,2.8214,1.8451,4.2959,7.2029,1.9869,0.1445,9.0551,0.6170])
plt.scatter(x_data,y_data)
plt.show()#设置学习率
lr=0.001
#截距相当于xita0
b=0
#斜率k,相当于xita1
k=0
#最大迭代次数
epochs=50
#自小二乘法,看代价函数(损失函数)定义的形式
def compute_error(b,k,x_data,y_data):
totalError=0
for i in range(0,len(x_data)):
#差平方
totalError+=(y_data[i]-(k*x_data[i]+b))**2
pass
return totalError/float(len(x_data))/2.0
#梯度下降法
def gradient_descent_runner(x_data,y_data,b,k,lr,epochs):
#计算总数量
m=float(len(x_data))
#循环epochs
for i in range(epochs):
b_grad=0
k_grad=0
#计算梯度综合再求平均
for j in range(0,len(x_data)):
#分别对西塔0和西塔1求骗到后的函数,
b_grad+=-(1/m)*(y_data[j]-((k*x_data[j])+b))
k_grad+=-(1/m)*x_data[j]*(y_data[j]-((k*x_data[j])+b))
#更新b和k
b=b-(lr*b_grad)
k=k-(lr*k_grad)
#没迭代5次,输出一次图像
# if i%5==0:
# print("epochs",i)
# plt.plot(x_data,y_data,'b.')
# plt.plot(x_data,k*k_data+b,'r')
# plt.show()
# pass
# pass
return b,k
# gradient_descent_runner(x_data,y_data,b,k,lr,epochs)print("Starting b={0},k={1},error={2}".format(b,k,compute_error(b,k,x_data,y_data)))
print("Running")
b,k=gradient_descent_runner(x_data,y_data,b,k,lr,epochs)
print("After{0} iterations b={1},k={2},error={3}".format(epochs,b,k,compute_error(b,k,x_data,y_data)))
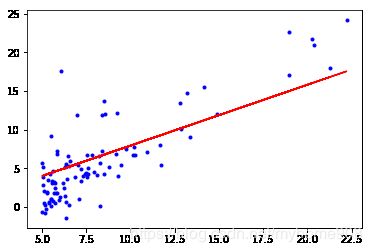
#画图
plt.plot(x_data,y_data,'b.')
#也就是y的值k*x_data+b
plt.plot(x_data, x_data*k+b, 'r')
plt.show()输出结果
Starting b=0,k=0,error=32.0306580806701
Running
After50 iterations b=0.04389983864403549,k=0.7881950216677549,error=5.726166012388302方法二:使用sklearn进行拟合
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
x_data=np.array([6.1101, 5.5277,8.5186, 7.0032, 5.8598, 8.3829,7.476, 8.5781, 6.4862,5.0546,5.7107, 14.1640,5.7340,8.4084, 5.6407, 5.3794, 6.3654,5.1301, 6.429,7.0708, 6.1891,20.2700, 5.4901, 6.3261, 5.5649, 18.9450, 12.8280, 10.9570, 13.1760, 22.2030, 5.2524, 6.5894, 9.2482, 5.8918, 8.2111, 7.9334, 8.0959, 5.6063, 12.8360, 6.3534, 5.4069,6.8825, 11.7080,5.7737, 7.8247, 7.0931, 5.0702, 5.8014,11.7000, 5.5416,7.5402,5.3077, 7.4239,7.6031,6.3328,6.3589,6.2742, 5.6397, 9.3102, 9.4536, 8.8254, 5.1793, 21.2790, 14.9080, 18.9590, 7.2182, 8.2951, 10.2360,5.4994,20.3410,10.1360,7.3345,6.0062,7.2259,5.0269, 6.5479, 7.5386, 5.0365, 10.2740, 5.1077,5.7292,5.1884, 6.3557,9.7687, 6.5159, 8.5172,9.1802,6.0020,5.5204, 5.0594, 5.7077,7.6366, 5.8707, 5.3054, 8.2934, 13.3940, 5.4369])
#取数据中所有的行,只要第一列
#y_data=data[:,1]
y_data=np.array([ 17.5920,9.1302,13.6620,11.8540,6.8233,11.8860,4.3483,12.0000,6.5987,3.8166,3.2522,15.5050,3.1551,7.2258,0.7162,3.5129,5.3048,0.5608,3.6518,5.3893,3.1386,21.7670,4.2630,5.1875,3.0825,22.6380,13.5010,7.0467,14.6920,24.1470,-.2200,5.9966,12.1340,1.8495,6.5426,4.5623,4.1164,3.3928,10.1170,5.4974,0.5566,3.9115,5.3854,2.4406,6.7318,1.0463,5.1337,1.8440,8.0043,1.0179,6.7504,1.8396,4.2885,4.9981,1.4233,-1.4211,2.4756,4.6042,3.9624,5.4141,5.1694,-0.7428,17.929,12.0540,17.0540,4.8852,5.7442,7.7754,1.0173,20.9920,6.6799,4.0259,1.2784,3.3411,-.6807,0.2968,3.8845,5.7014,6.7526,2.0576,0.4795,0.2042,0.6786,7.5435,5.3436,4.2415,6.7981,0.9270,0.1520,2.8214,1.8451,4.2959,7.2029,1.9869,0.1445,9.0551,0.6170])
plt.scatter(x_data,y_data)
plt.show()
#一维,97个数据
print(x_data.shape)x_data=x_data.reshape(97,1)
y_data=y_data.reshape(97,1)#需要将一维的变为二维的,这样才可以使用库中的函数进行预测
model=LinearRegression()
model.fit(x_data,y_data)
plt.plot(x_data,y_data,'b.')
#model.predict(x_data)就是预测的y值
plt.plot(x_data,model.predict(x_data),'r')
plt.show()