主题模型TopicModel：PLSA模型及PLSA的EM推导

http://blog.csdn.net/pipisorry/article/details/42560877

Introduction:

        概率潜在语义分析简称pLSA(Probabilisticlatent semantic analysis)基于双模式和共现的数据分析方法延伸的经典的统计学方法。概率潜在语义分析应用于信息检索，过滤，自然语言处理，文本的机器学习或者其他相关领域。

        概率潜在语义分析与标准潜在语义分析的不同是，标准潜在语义分析是以共现表（就是共现的矩阵）的奇异值分解的形式表现的，而概率潜在语义分析却是基于派生自LCM的混合矩阵分解。考虑到word和doc共现形式，概率潜在语义分析基于多项式分布和条件分布的混合来建模共现的概率。所谓共现其实就是W和D的一个矩阵，所谓双模式就是在W和D上同时进行考虑。基于概率统计的PLSA模型，用EM算法学习模型参数。

PLSA的建模——层面模型

层面模型就是关联于潜在类Z的共现表的潜在可变模型。在层面模型中，文档被视为潜在的K个层面的混合。每一个层面就是word对于z(潜在类)的概率分布。

PLSA的建模——数据的共现

对于每一组（w,d）都使之与潜在变量z关联。

PLSA的建模——预测words

已经的是文档的概率，首先要计算潜在类Z根据条件概率D，生成单词W根据条件概率Z。

PLSA的公式：

P(w,d) =

∑

P(c)P(d | c)P(w | c) = P(d)

∑

P(c | d)P(w | c)

注：这里的C和上面说的Z是一样的。

公式解析：第一个公式是对称公式，在这个公式中,W和D都是以相同的方式（都用了W和D基于C的条件概率）通过潜在类C处理的。第二个公式是非对称公式。在这个公式中，对于每一个D，先根据D的条件概率计算C，然后根据C的条件概率计算W。事实上，这个公式可以扩展成计算任何一对离散变量的共现。因为我们的W和D是已知的，但是Z是未知的，所以我们的重心放在求Z上。那么如何求Z呢？

PLSA的概率图模型如下

其中D代表文档，Z代表隐含类别或者主题，W为观察到的单词，表示单词出现在文档的概率，表示文档中出现主题下的单词的概率，给定主题出现单词的概率。并且每个主题在所有词项上服从Multinomial 分布，每个文档在所有主题上服从Multinomial 分布。

整个文档的生成过程：

(1) 以的概率选中文档；

(2) 以的概率选中主题；

(3) 以的概率产生一个单词。

我们可以观察到的数据就是对，而是隐含变量。

的联合分布为

而和分布对应了两组Multinomial 分布，我们需要估计这两组分布的参数。下面给出用EM算法估计PLSA参数的详细推导过程。

Estimate parameters in PLSA  by EM

目标parameters有：、  -

如文本语言模型的参数估计-最大似然估计、MAP及贝叶斯估计一文所述，常用的参数估计方法有MLE、MAP、贝叶斯估计等等。

但是在PLSA中，如果我们试图直接用MLE来估计参数，就会得到似然函数

    { 由于文档长度可以单独计算，所以去掉它不影响 }

其中是单词出现在文档中的次数。

注意这是一个关于和的函数，一共有N*K + M*K个自变量，如果直接对这些自变量求偏导数，我们会发现由于自变量包含在对数和中，这个方程的求解很困难。因此对于这样的包含“隐含变量”或者“缺失数据”的概率模型参数估计问题，我们采用EM算法。

EM算法的步骤是：

(1)E步骤：求隐含变量Given当前估计的参数条件下的后验概率。

(2)M步骤：最大化Complete data对数似然函数的期望，此时我们使用E步骤里计算的隐含变量的后验概率，得到新的参数值。

两步迭代进行直到收敛。

{在PLSA中，Incomplete data 是观察到的，隐含变量是主题，那么complete data就是三元组}

针对我们PLSA参数估计问题

在E步骤中，直接使用贝叶斯公式计算隐含变量在当前参数取值条件下的后验概率，有

在这个步骤中，我们假定所有的和都是已知的，初始时随机赋值，后面迭代的过程中取前一轮M步骤中得到的参数值。

在M步骤中，我们最大化Complete data对数似然函数的期望(即把其中与z相关的部分积分掉），见【TopicModel - EM算法】）。其期望是

   {TopicModel - EM算法 - Lazy Statistician规则：E(z) = ∑P（zk|di, wj)z中z替换成L式， 相当于把其中与z相关的部分积分掉}

注意这里是已知的，取得是前面E步骤里面的估计值。下面我们来最大化期望，这又是一个多元函数求极值的问题，可以用拉格朗日乘数法。

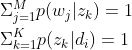拉格朗日乘数法可以把条件极值问题转化为无条件极值问题，在PLSA中目标函数就是,约束条件是（1）

由此我们可以写出拉格朗日函数

这是一个关于和的函数，分别对其求偏导数，我们可以得到（对求导，j、k固定值）

（2）

{注意这里进行过方程两边同时乘以和的变形}，联立上面4组方程（1）（2），我们就可以解出M步骤中通过最大化期望估计出的新的参数值

{解方程组的关键在于先求出,其实只需要做一个加和运算就可以把的系数都化成1，后面就好计算了}

然后使用更新后的参数值，我们又进入E步骤，计算隐含变量 Given当前估计的参数条件下的后验概率。如此不断迭代，直到满足终止条件。

注意到我们在M步骤中还是使用对Complete Data的MLE，那么如果我们想加入一些先验知识进入我们的模型，我们可以在M步骤中使用MAP估计。正如文本语言模型的参数估计-最大似然估计、MAP及贝叶斯估计中投硬币的二项分布实验中我们加入“硬币一般是两面均匀的”这个先验一样。而由此计算出的参数的估计值会在分子分母中多出关于先验参数的preduo counts,其他步骤都是一样的。具体可以参考Mei Qiaozhu 的Notes。

http://blog.csdn.net/pipisorry/article/details/42560877

Estimate parameters in a simple mixture unigram language model by EM

在PLSA的参数估计中，我们使用了EM算法。EM算法经常用来估计包含“缺失数据”或者“隐含变量”模型的参数估计问题。这两个概念是互相联系的，当我们的模型中有“隐含变量”时，我们会认为原始数据是“不完全的数据”，因为隐含变量的值无法观察到；反过来，当我们的数据incomplete时，我们可以通过增加隐含变量来对“缺失数据”建模。

为了加深对EM算法的理解，下面我们来看如何用EM算法来估计一个简单混合unigram语言模型的参数。

最大似然估计与隐含变量引入

        所谓unigram语言模型，就是构建语言模型是抛弃所有上下文信息，认为一个词出现的概率与其所在位置无关，具体概率图模型可以参见LDA及Gibbs Samping一文中的介绍。

通俗的说混合概率模型就是由最基本的概率分布比如正态分布、多元分布等经过线性组合形成的新的概率模型，比如混合高斯模型就是由K个高斯分布线性组合而得到。混合模型中产生数据的确切“component model”对我们是隐藏的。

我们假设混合模型包含两个multinomial component model,一个是背景词生成模型,另一个是主题词生成模型。注意这种模型组成方式在概率语言模型中很常见，比如在TwitterLDA中使用的背景词和主题词两个多元分布；TimeUserLDA中使用的Global Topic 和Personal Topic两个多元分布，都是这类模型。为了表示单词是哪个模型生成的，我们会为每个单词增加一个布尔类型的控制变量。

文档的对数似然函数为

为第i个文档中的第j个词，为表示文档中背景词比例的参数，通常根据经验给定。因此是已知的，我们只需要估计即可。

同样的我们首先试图用最大似然估计来估计参数。也就是去找最大化似然函数的参数值，有

这是一个关于的函数，同样的，包含在了对数和中。因此很难求解极大值，用拉格朗日乘数法，你会发现偏导数等于0得到的方程很难求解。所以我们需要依赖数值算法，而EM算法就是其中常用的一种。

我们为每个单词引入一个布尔类型的变量z表示该单词是background word 还是topic word.即

这里我们假设”complete data”不仅包含可以观察到F中的所有单词，而且还包括隐含的变量z。那么根据EM算法，在E步骤我们计算“complete data”的对数似然函数有

比较一下和，求和运算在对数之外进行，因为此时通过控制变量z的设置，我们明确知道了单词是由背景词分布还是topic 词分布产生的。

和的关系是怎样的呢？如果带估计参数是,原始数据是X，对于每一个原始数据分配了一个隐含变量H，则有

似然函数的下界分析

EM算法的基本思想就是初始随机给定待估计参数的值，然后通过E步骤和M步骤两步迭代去不断搜索更好的参数值。更好的参数值应该要满足使得似然函数更大。我们假设一个潜在的更好参数值是，第n次迭代M步骤得到的参数估计值是,那么两个参数值对应的似然函数和”complete data”的似然函数的差满足

我们寻找更好参数值的目标就是要最大化,也等价于最大化。我们来计算隐含变量在给定当前数据X和当前估计的参数值条件下的条件概率分布即，有

其中右边第三项是和的相对熵，总为非负值。因此我们有

于是我们得到了潜在更好参数值的incomplete data似然函数的下界。这里我们尤其要注意右边后两项为常数，因为不包含。所以incomplete data似然函数的下界就是complete data似然函数的期望，也就是诸多EM算法讲义中出现的Q函数，表达式为

可以看出这个期望等于complete data似然函数乘以对应隐含变量条件概率再求和。对于我们要求解的问题，Q函数就是

这里多解释几句Q函数。单词相应的变量z为0时，单词为topic word,从多元分布中产生；当z为1时，单词为background word,从多元分布产生。同时我们也可以看到如何求Q函数即complete data似然函数的期望，也就是我们要最大化的那个期望(EM算法最大化期望指的就是这个期望)，我们要特别关注隐含变量在观察到数据X和前一轮估计出的参数值条件下取不同值的概率，而隐含变量不同的值对应complete data的不同的似然函数，我们要计算的所谓的期望就是指complete data的似然函数值在不同隐含变量取值情况下的期望值。

EM算法的一般步骤

通过上面部分的分析，我们知道，如果我们在下一轮迭代中可以找到一个更好的参数值使得

那么相应的也会有，因此EM算法的一般步骤如下

(1) 随机初始化参数值，也可以根据任何关于最佳参数取值范围的先验知识来初始化。

(2) 不断两步迭代寻找更优的参数值：

(a) E步骤（求期望） 计算Q函数

(b)M步骤（最大化）通过最大化Q函数来寻找更优的参数值

(3) 当似然函数收敛时算法停止。

这里需要注意如何尽量保证EM算法可以找到全局最优解而不是局部最优解呢？第一种方法是尝试许多不同的参数初始值，然后从得到的很多估计出的参数值中选取最优的；第二种方法是通过一个更简单的模型比如只有唯一全局最大值的模型来决定复杂模型的初始值。

通过前面的分析可以知道，EM算法的优势在于complete data的似然函数更容易最大化，因为已经假定了隐含变量的取值，当然要乘以隐含变量取该值的条件概率，所以最终变成了最大化期望值。由于隐含变量变成了已知量，Q函数比原始incomplete data的似然函数更容易求最大值。因此对于“缺失数据”的情况，我们通过引入隐含变量使得complete data的似然函数容易最大化。

在E步骤中，主要的计算难点在于计算隐含变量的条件概率，在PLSA中就是

在我们这个简单混合语言模型的例子中就是

我们假设z的取值只于当前那一个单词有关，计算很容易，但是在LDA中用这种方法计算隐含变量的条件概率和最大化Q函数就比较复杂，可以参见原始LDA论文的参数推导部分。我们也可以用更简单的Gibbs Sampling来估计参数，具体可以参见LDA及Gibbs Samping。

继续我们的问题，下面便是M步骤。使用拉格朗日乘数法来求Q函数的最大值，约束条件是

构造拉格朗日辅助函数

对自变量求偏导数

令偏导数为0解出来唯一的极值点

容易知道这里唯一的极值点就是最值点了。注意这里Zhai老师变换了一下变量表示，把对文档里面词的遍历转化成了对词典里面的term的遍历，因为z的取值至于对应的那一个单词有关，与上下文无关。因此E步骤求隐含变量的条件概率公式也相应变成了

最后我们就得到了简单混合Unigram语言模型的EM算法更新公式

即E步骤 求隐含变量条件概率和M步骤 最大化期望估计参数的公式

整个计算过程我们可以看到，我们不需要明确求出Q函数的表达式。取而代之的是我们计算隐含变量的条件概率，然后通过最大化Q函数来得到新的参数估计值。

因此EM算法两步迭代的过程实质是在寻找更好的待估计参数的值使得原始数据即incomplete data似然函数的下界不断提升，而这个“下界“就是引入隐含变量之后的complete data似然函数的期望，也就是诸多EM算法讲义中出现的Q函数，通过最大化Q函数来寻找更优的参数值。同时，上一轮估计出的参数值会在下一轮E步骤中当成已知条件计算隐含变量的条件概率，而这个条件概率又是最大化Q函数求新的参数值是所必需的。

【EM算法Notes】

PLSA模型的缺点

plsa过拟合现象

PLSA有时会出现过拟合的现象。所谓过拟合（Overfit），是这样一种现象：一个假设在训练数据上能够获得比其他假设更好的拟合，但是在训练数据外的数据集上却不能很好的拟合数据。此时我们就叫这个假设出现了overfit的现象。

原因

出现这种现象的主要原因是训练数据中存在噪音或者训练数据太少。

解决方法

要避免过拟合的问题，PLSA使用了一种广泛应用的最大似然估计的方法，期望最大化。PLSA中训练参数的值会随着文档的数目线性递增。PLSA可以生成其所在数据集的的文档的模型，但却不能生成新文档的模型。通过修改EM（期望最大化）的算法来避免这个问题，我么把这个算法称为强化的期望最大化算法（tempered EM）。强化的期望最大化算法中引入了控制参数beta。Beta值起始是1，紧着逐渐减少。引入beta的目的就是为了避免过拟合的问题，在beta中，过拟合和不充分拟合的状态被定义。具体的算法是：让beta的初始值为1，然后根据待训练数据来测试模型，如果成功，则使用该beta，如果不成功，则收敛。收敛的意思就是使得beta = n*beta， n<1。

from:http://blog.csdn.net/pipisorry/article/details/42560877

ref:TopicModel - EM算法

wiki - Probabilistic latent semantic analysis

关于PLSA