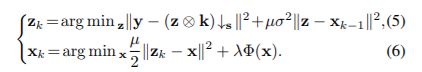CVPR2020: Deep Unfolding Network for Image Super-Resolution
论文地址:https://arxiv.org/pdf/2003.10428.pdf
作者认为,基于模型(model-based)的方法适合处理不同的尺寸,模糊核和噪声水平的单张图像的超分辨率问题。相比之下,基于学习的方法(learning-based)普遍缺少这种灵活性。这篇文章结合了基于模型和基于学习的两种方法,提出了一种端到端的unfolding network:USRNet(deep unfolding superresolution network)。
Contribution:
- USRNet是第一个尝试处理经典退化模型与不同的尺度因子,模糊内核和噪声水平通过一个单一的端到端训练模型。
- 为弥合基于模型方法和基于学习的方法之间的差距提供了途径。
- 本质上强加了一个降级约束(即,估计的HR图像应符合退化过程)和一个先验约束(即,估计的HR图像应该具有自然特征)上的解决方案。
- 在不同退化设置的LR图像上表现良好,显示了巨大的实际应用潜力。
Contribution理解:
第一点和第三点可以认为是model-based带来的优势。
第二点解读:
我们知道,常规的迭代算法通常可以分为一些子问题进行求解,然后通过若干次迭代进行更新。这篇文章的套路就是把每次迭代变成神经网络的一层,将多次迭代的过程变成神经网络的若干个层。每个子问题的求解,在神经网络里就变成一层网络里的一个子模块。这也是model-based问题用learning-based框架来解决的常见方法。
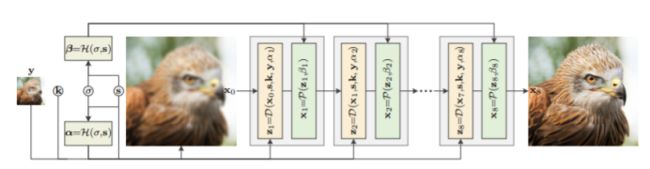
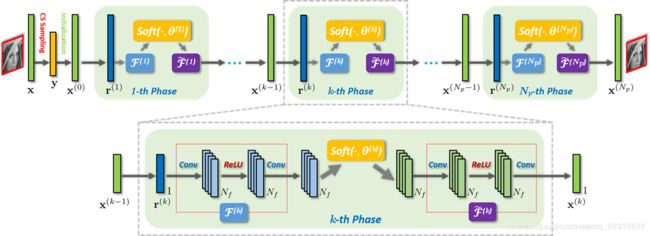
理解了第二点,整个网络结构就呼之欲出了:
这种combined learning-based和model-based网络的本质通常在于将iteration algorithm 通过unfolding 的方式变成神经网络,可以通过backward使得算法中handcraft的参数变的learnable。这种网络让我想起,2018年ISTA-Net文章就提到过类似的unfolding方法(见下图),当然这种思想都是通用的。
然后就是本文具体每一层的子模块了。既然是model-based的subproblem,往往就是建模型-建立子问题-求解子问题-改成网络子模块四步。
本文也不例外。
首先,图像恢复模型,数据项,正则项:
第二,建立子问题。 数据项,先验项分别求解,自然分成了两个子问题。
两个子问题当然就对应上面网络里每一层的两个子模块了。
第三,求解子问题。 就是解决(5)(6)两个式子。
1.更新 z z z(数据项): 文章采用频域fft解法。
2.更新 x x x (先验项): 通常和先验有关,文章里写的很少(就三行):从贝叶斯的角度来看,它实际上对应于某个噪声水平的去噪问题。
第四,子问题变成网络的子模块。
1. z z z(数据项)子模块Data module:
class DataNet(nn.Module):
def __init__(self):
super(DataNet, self).__init__()
def forward(self, x, FB, FBC, F2B, FBFy, alpha, sf):
FR = FBFy + torch.rfft(alpha*x, 2, onesided=False)
x1 = cmul(FB, FR)
FBR = torch.mean(splits(x1, sf), dim=-1, keepdim=False)
invW = torch.mean(splits(F2B, sf), dim=-1, keepdim=False)
invWBR = cdiv(FBR, csum(invW, alpha))
FCBinvWBR = cmul(FBC, invWBR.repeat(1, 1, sf, sf, 1))
FX = (FR-FCBinvWBR)/alpha.unsqueeze(-1)
Xest = torch.irfft(FX, 2, onesided=False)
return Xest
可以看出,这部分和频域fft解法是对应的,每层都有训练参数 α \alpha α
2. x x x(先验项)子模块Prior Module:基于U-Net和Residual block的去噪,用来handle various noise levels via a single model。
放代码:class ResUNet(nn.Module):
def __init__(self, in_nc=4, out_nc=3, nc=[64, 128, 256, 512], nb=2, act_mode='R', downsample_mode='strideconv', upsample_mode='convtranspose'):
super(ResUNet, self).__init__()
self.m_head = B.conv(in_nc, nc[0], bias=False, mode='C')
# downsample
if downsample_mode == 'avgpool':
downsample_block = B.downsample_avgpool
elif downsample_mode == 'maxpool':
downsample_block = B.downsample_maxpool
elif downsample_mode == 'strideconv':
downsample_block = B.downsample_strideconv
else:
raise NotImplementedError('downsample mode [{:s}] is not found'.format(downsample_mode))
self.m_down1 = B.sequential(*[B.ResBlock(nc[0], nc[0], bias=False, mode='C'+act_mode+'C') for _ in range(nb)], downsample_block(nc[0], nc[1], bias=False, mode='2'))
self.m_down2 = B.sequential(*[B.ResBlock(nc[1], nc[1], bias=False, mode='C'+act_mode+'C') for _ in range(nb)], downsample_block(nc[1], nc[2], bias=False, mode='2'))
self.m_down3 = B.sequential(*[B.ResBlock(nc[2], nc[2], bias=False, mode='C'+act_mode+'C') for _ in range(nb)], downsample_block(nc[2], nc[3], bias=False, mode='2'))
self.m_body = B.sequential(*[B.ResBlock(nc[3], nc[3], bias=False, mode='C'+act_mode+'C') for _ in range(nb)])
# upsample
if upsample_mode == 'upconv':
upsample_block = B.upsample_upconv
elif upsample_mode == 'pixelshuffle':
upsample_block = B.upsample_pixelshuffle
elif upsample_mode == 'convtranspose':
upsample_block = B.upsample_convtranspose
else:
raise NotImplementedError('upsample mode [{:s}] is not found'.format(upsample_mode))
self.m_up3 = B.sequential(upsample_block(nc[3], nc[2], bias=False, mode='2'), *[B.ResBlock(nc[2], nc[2], bias=False, mode='C'+act_mode+'C') for _ in range(nb)])
self.m_up2 = B.sequential(upsample_block(nc[2], nc[1], bias=False, mode='2'), *[B.ResBlock(nc[1], nc[1], bias=False, mode='C'+act_mode+'C') for _ in range(nb)])
self.m_up1 = B.sequential(upsample_block(nc[1], nc[0], bias=False, mode='2'), *[B.ResBlock(nc[0], nc[0], bias=False, mode='C'+act_mode+'C') for _ in range(nb)])
self.m_tail = B.conv(nc[0], out_nc, bias=False, mode='C')
def forward(self, x):
h, w = x.size()[-2:]
paddingBottom = int(np.ceil(h/8)*8-h)
paddingRight = int(np.ceil(w/8)*8-w)
x = nn.ReplicationPad2d((0, paddingRight, 0, paddingBottom))(x)
x1 = self.m_head(x)
x2 = self.m_down1(x1)
x3 = self.m_down2(x2)
x4 = self.m_down3(x3)
x = self.m_body(x4)
x = self.m_up3(x+x4)
x = self.m_up2(x+x3)
x = self.m_up1(x+x2)
x = self.m_tail(x+x1)
x = x[..., :h, :w]
return x
3.除了上面两个模块以外,文章还提出了超参数模块 Hyper-parameter module,作为一个“滑条”来控制数据模块和先验模块的输出,是对以上两个模块的补正。它实际位于上面两个子模块的内部。
class HyPaNet(nn.Module):
def __init__(self, in_nc=2, out_nc=8, channel=64):
super(HyPaNet, self).__init__()
self.mlp = nn.Sequential(
nn.Conv2d(in_nc, channel, 1, padding=0, bias=True),
nn.ReLU(inplace=True),
nn.Conv2d(channel, channel, 1, padding=0, bias=True),
nn.ReLU(inplace=True),
nn.Conv2d(channel, out_nc, 1, padding=0, bias=True),
nn.Softplus())
def forward(self, x):
x = self.mlp(x) + 1e-6
return x
最后是USRNet整体结构:
class USRNet(nn.Module):
def __init__(self, n_iter=8, h_nc=64, in_nc=4, out_nc=3, nc=[64, 128, 256, 512], nb=2, act_mode='R', downsample_mode='strideconv', upsample_mode='convtranspose'):
super(USRNet, self).__init__()
self.d = DataNet()
self.p = ResUNet(in_nc=in_nc, out_nc=out_nc, nc=nc, nb=nb, act_mode=act_mode, downsample_mode=downsample_mode, upsample_mode=upsample_mode)
self.h = HyPaNet(in_nc=2, out_nc=n_iter*2, channel=h_nc)
self.n = n_iter
def forward(self, x, k, sf, sigma):
'''
x: tensor, NxCxWxH
k: tensor, Nx(1,3)xwxh
sf: integer, 1
sigma: tensor, Nx1x1x1
'''
# initialization & pre-calculation
w, h = x.shape[-2:]
FB = p2o(k, (w*sf, h*sf))
FBC = cconj(FB, inplace=False)
F2B = r2c(cabs2(FB))
STy = upsample(x, sf=sf)
FBFy = cmul(FBC, torch.rfft(STy, 2, onesided=False))
x = nn.functional.interpolate(x, scale_factor=sf, mode='nearest')
# hyper-parameter, alpha & beta
ab = self.h(torch.cat((sigma, torch.tensor(sf).type_as(sigma).expand_as(sigma)), dim=1))
# unfolding
for i in range(self.n):
x = self.d(x, FB, FBC, F2B, FBFy, ab[:, i:i+1, ...], sf)
x = self.p(torch.cat((x, ab[:, i+self.n:i+self.n+1, ...].repeat(1, 1, x.size(2), x.size(3))), dim=1))
return x
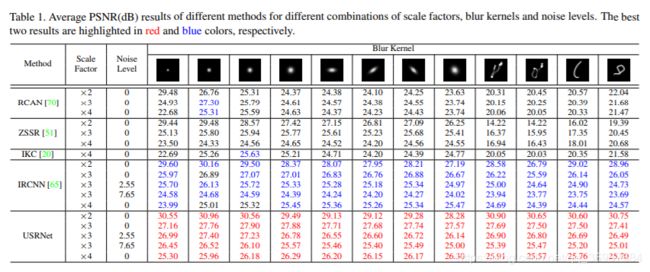
Results
可以看出,文章在处理超分辨率、去噪的联合问题上更有优势。