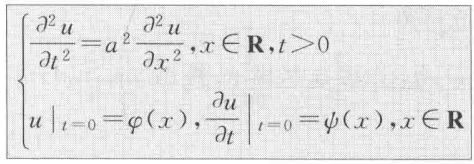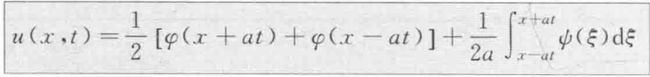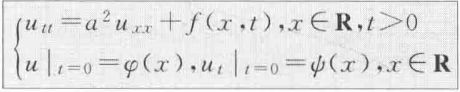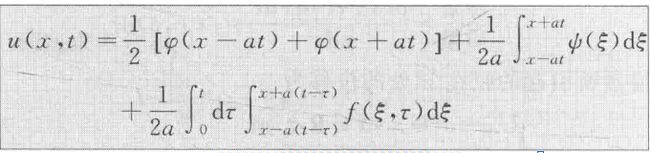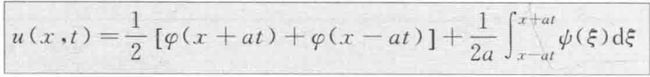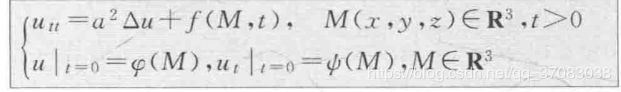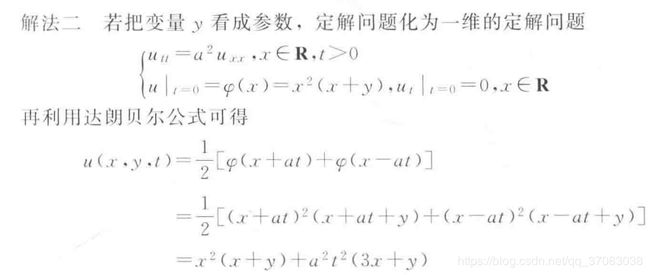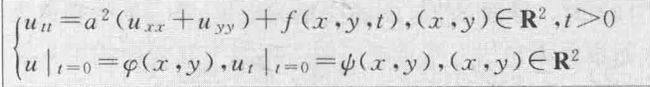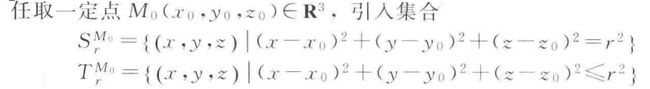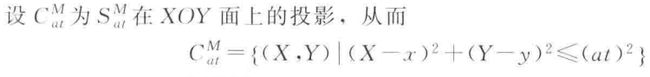数学物理方程 第三章 行波法

3.1 一维波动

3.1.1 无界弦的自由振动

----------------------

定解问题：范定方程+条件

先利用公式求解范定方程，得到u的通解

再带入条件，得到u的定解

----------------------------

定解问题

求出的定解

该定解称为无限长弦的自由振动的达朗贝尔公式

 

3.1.2 齐次化原理/冲量原理/外力化初速度原理      用于求解非齐次式

 

3.1.3 无界弦的受迫振动   利用杜哈梅原理求解

将该定解问题分解为两个子定解问题

子问题1直接求解得u1，子问题2利用杜哈梅原理求解得u2，u=u1+u2

该解称为无限长弦的受迫振动的达朗贝尔公式

 

3.1.4  达朗贝尔公式的意义

这是齐次问题的解，非齐次也一样问题解的意义也一样

φ为波，φ(x+at)为左行波  φ(x-at)为右行波

达朗贝尔公式表示：解是左行波与右行波的平均值再加上一些其它项

 

 

 

3.1.5 特征线

一维波动方程的特征方程是：dx/dt=±a

则特征线为 x±at=C

过点(x0,t0)的两条特征线为 x+a*t=x0+a*t0   x-a*t=x0-a*t0

 

3.1.6 依赖区间

u只依赖于初始函数φ与ψ在区间 x0-a*t0到x0+a*t0 上的取值

称[x0-a*t0,x0+a*t0]为点(x0,t0)的依赖区间

 

3.1.7 决定区域

过点[x1,0] 做两条特征线 x+a*t=x1 x-a*t=x1

过点[x2,0] 做两条特征线 x+a*t=x2   x-a*t=x2

会有两条特征线交到一起，这个三角形区域称为[x1, x2]的决定区域

即定义在[x1, x2]上的初始函数φ与ψ，决定该三角形区域内的u

 

3.1.8 影响区域

会有两条特征线未交到一起，这个区域称为[x1, x2]的影响区域

即定义在[x1, x2]上的初始函数φ与ψ，影响该区域内的u

 

 

 

 

3.2 空间波动问题

定解问题： 三维波动方程+初始条件

定解

该解称为三维齐次波动问题的泊松公式

 

 

定解问题：三维波动方程+第一类边值条件

定解

u=x+y+z

 

 

定解问题：二维波动方程+初始条件

定解

该解称为二维齐次波动问题的泊松公式

注：由三维推出二维定解问题的方法称为降维法

 

定解问题：二维波动方程+第一类边值条件

定解

u=x**2*(x+y)+(a**2)*(t**2)*(3x+y)

附上解法，即令 z=x**2*(x+y)，求解出关于z的达朗贝尔公式，再将 z=x**2*(x+y)带入

 

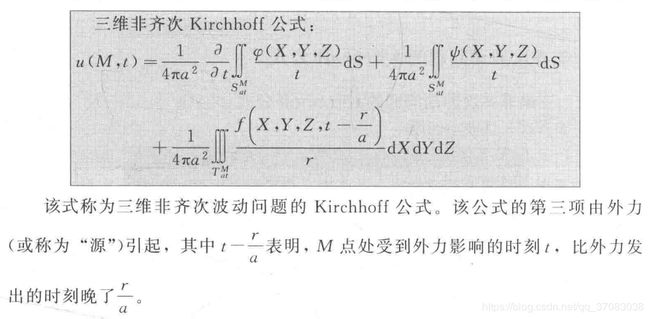
3.2.3 非齐次波动问题的Kirchhoff公式

定解问题：三维非齐次波动方程 + 初始条件

定解，由杜哈梅原理和三维波动泊松公式求解

该解称为三维非齐次波动问题的Kirchhoff公式

 

 

定解问题：二维非齐次波动方程 + 初始条件

定解

 

 

注：所引入的集合的含义

S表示球面  T表示球的内部 

 

C表示球面S在XOY面的投影，所以C是一个圆面

 

4.2.4 波动问题的物理意义

三维与二维泊松方程的解的取值区域，前者是球面S 后者是圆面C。

三维空间中，局部的初始扰动会有波前也有波后，即波会很明显的产生与消失；但二维空间中，只有波前，即波会很明显的产生但不会消失，不过会随着t衰减，但不会消失。

 

imagination：

三维空间有一区域R**3，此时有一个球面波慢慢接近，当球面与该区域交上，即表示该区域有波产生，当球面波继续传播，与该区域不交，即表示该区域波消失。

二维空间有一区域R**2，此时有一个圆面波慢慢接近，当圆面与该区域交上，即表示该区域有波产生，当球面波继续传播，始终与该区域交上，表示该区域始终有波产生。

 

黑色的是波  红色的是前方的区域

波传播到了红色区域处，可以看出波始终与红色区域相交，即表示红色区域始终有波

水面波大体为二维波。

无法利用二维波传递信息。