B站学习法之深度学习笔记一

Three Steps for Deep Learning

Step 1. A neural network is a function compose of simple functions (neurons)
神经元=simple fcn
神经网络=fcn
    通常需要自己决定网络的structure,and let machine find parameters from data.
    所以我们要focused 就是有哪些常见的structure.
Step 2. 定好structure和para后就要定cost function——什么样的network参数是好的？什么样的network的参数又是不好的？那么如何定cost fcn呢？
    那当然是case by case，取决于你要处理的问题和你手上的data（训练数据）
Step 3. 有了上面两个步骤之后，我们就用gradient descent(梯度下降）找到一个最好的fcn

接下来开头课程的outline

1.Fully connected layer(全连接层)

1.1关于全连接层的浅显理解

对全连接层的理解参考了这篇原创文章[link]https://blog.csdn.net/m0_37407756/article/details/80904580
理解：例如经过卷积，relu后得到3x3x5的输出。
那它是怎么样把3x3x5的输出，转换成1x4096的形式？

很简单,可以理解为在中间做了一个卷积。

从上图我们可以看出，我们用一个3x3x5的filter 去卷积激活函数的输出，得到的结果就是一个fully connected layer 的一个神经元的输出，这个输出就是一个值。因为我们有4096个神经元。我们实际就是用一个3x3x5x4096的卷积层去卷积激活函数的输出。

以VGG-16再举个例子吧，

对224x224x3的输入，最后一层卷积可得输出为7x7x512，如后层是一层含4096个神经元的FC，则可用卷积核为7x7x512x4096的全局卷积来实现这一全连接运算过程。

它把特征representation整合到一起，输出为一个值。

那么全连接层这样做,有什么好处？
好处就是大大减少特征位置对分类带来的影响，不能理解？没关系，继续举例理解：
举个简单的例子：

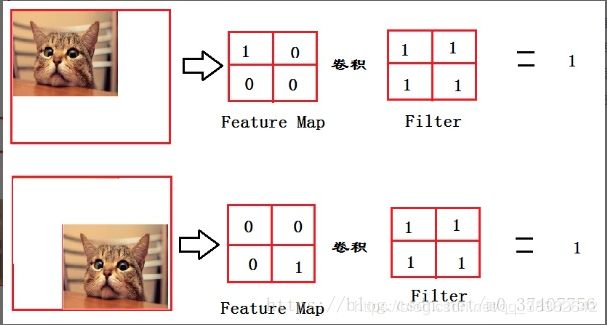
从上图我们可以看出，猫在不同的位置，输出的feature值相同，但是位置不同。

对于电脑来说，特征值相同，但是特征值位置不同，那分类结果也可能不一样。所以为了避免上图中Feature Map的位置不同引起电脑分类不一样的后果，全连接层filter的作用就相当于告诉电脑——

喵在哪我不管，我只要喵，于是我让filter去把这个喵找到，实际就是把Feature map 整合成一个值，这个值大，有喵，这个值小，那就可能没喵，和这个喵在哪关系不大了，鲁棒性有大大增强。

在实际使用当中，全连接层中一层的一个神经元可以看成一个多项式，我们用许多神经元去拟合数据分布。但是只用一层fully connected layer 有时候没法解决非线性问题，那么如果有两层或以上fully connected layer就可以很好地解决非线性问题了

再举一个例子说明很好地解决非线性问题：
我们都知道，全连接层之前的作用是提取特征

全连接层的作用是分类

我们现在的任务是去区别一图片是不是猫

假设现在神经网络模型已经训练完了，全连接层已经知道了，并表示：当我们检测到以下特征时，我就可以判断这个东东是猫了。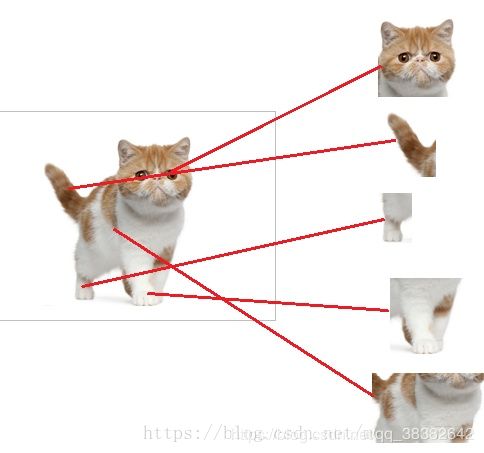
因为全连接层的作用主要就是实现分类（Classification）

从下图，我们可以看出

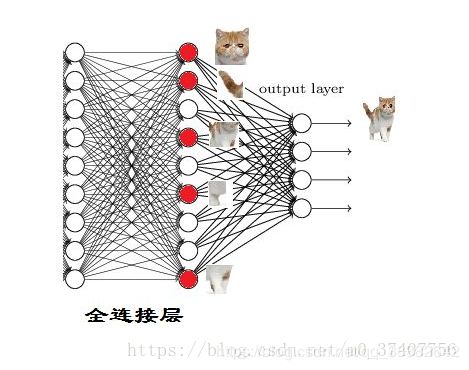
红色的神经元表示这个特征被找到了（激活了）
同一层的其他神经元，要么猫的特征不明显，要么没找到
当我们把这些找到的特征组合在一起后发现最符合要求的是猫——ok，我认为这是猫了。

再比如说区别猫头：

道理和区别猫一样
当我们找到这些特征，神经元就被激活了（上图红色圆圈）

注：这些细节特征又是怎么来的？——是从前面的卷积层，下采样层来的

全连接层参数特多（可占整个网络参数80%左右），那么全连接层对模型影响参数就是三个：

1. 全连接层的总层数（长度）
2. 单个全连接层的神经元数（宽度）
3. 激活函数
   其中，激活函数暂时先明白他的作用是
   
       以上，从全连接层的好处（减少特征位置对分类带来的影响）+全连接层的作用（分类）+全连接层对模型影响的主要参数进行了十分浅显且不知道恰不恰当的举例，对Fully connected layer有了粗浅的了解。

1.2关于全连接层的浅显理解

    第$l$层有N个Nodes,均对用一个output:$a_i^l$,其中$i$代表第$l$层的第$i$个神经元的输出
    把一层layer中的所有output集合起来——就组成了一个vector向量，用$a^l$代表第$l$层的输出向量。

    FCL中的每个layer都是两两相接的，那neurons和neurons之间的connection有一个weight——$w_{ij}^l$
其中，上标表示这个连接了第l-1个layer和第l个Layer；下标是指这个weight连接了第$l-1$个layer的第$j$个neuron$a_j$连接到（箭头指向）第$l$个layer的第$i$个neuron.($j$在左边，$i$在右边）

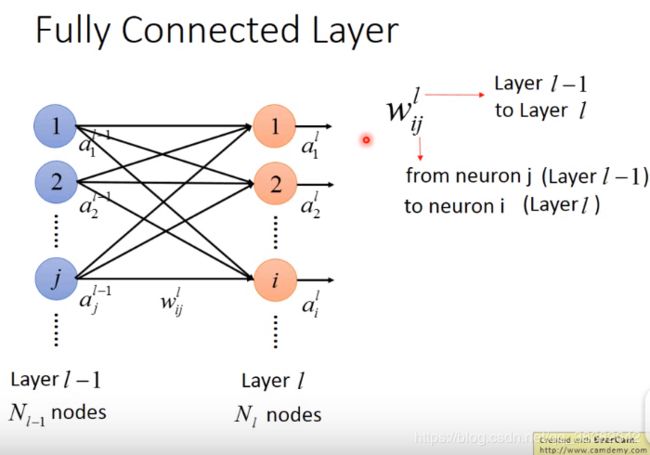
    依次类推，两两neurons之间就有一个weight，由此排成一个矩阵$W^l$.第一个index(即$i$)指的是row,第二个index(即$j$)指的是column.从而$W^l$的row行的个数就是$N_l$(节点数），$W^l$的column列的个数就是$N_{l-1}$(节点数）
（注：第一个index指的是上图的input layer,第二个index指的是上图的output layer）

    那么，现在就构造了一个matrix将所有的weight全都表示。上标$l$表示第$l-1$和第$l$层的weight_matrix.
    除了weight以外，每个neuron还有一个bias.（我们可以把bias想象成weight的一部分，只是需要在input的地方多加一个1（如下图所示的1，并将1视为是weight的一部分），所以有些书就没有给出bias图线的部分）将这些bias全部穿起来成一个vector,用$b^l$表示第$l$个layer组成的bias的vector.

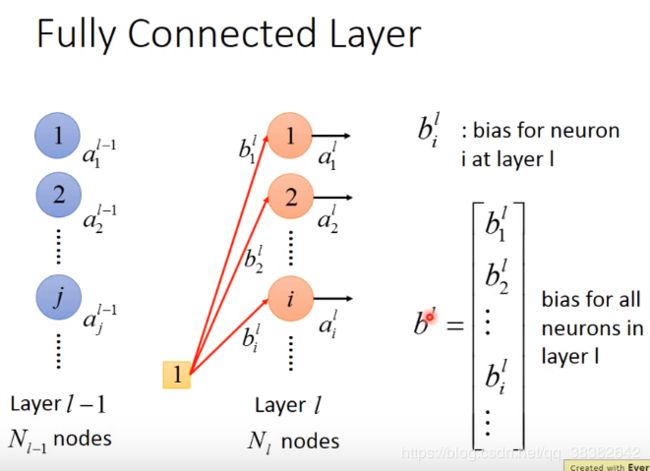
接下来我们要算$a_i^l$,即第$l$个layer的第$i$个neuron的output$a_i^l$,和前一层$l-1$对应的output$a_j^{l-1}$有什么样的关系。
在计算上面这个关系之前，我们必须先计算$z_i^l$(input of the activation function for neuron i at layer l),同样，我们用$z^l$表示layer $l-1$到layer $l$的所有$z_i^l$构成的vector.
$z_i^l$与他前面层所有的output的关系式
$$z_i^l=w_{i1}^l{a}_1^{l-1}+w_{i2}^l{a}_2^{l-1}+...+b_i^l$$
(即前一层各个neuron的output乘上对应的weight后再加上最后1发出的bias,$w_{i1}^l$表示前层的第1个neuron到后层第i个neuron对用的权重)

    现在考虑$l$一整个layer的output,那就要考虑$a^{l-1}$和$a^l$之间的关系，但是计算他们关系这之前，要先计算一下$z^l$与$a^{l-1}$的关系。

    如果ij相反的话，即index反过来，那就要将$W^l$加转置transport。
以上计算了$Z^l$与$a^{l-1}$的关系，那接下来要计算$Z^l$与$a^l$的关系，从而得到$a^{l-1}$与$a^l$的关系。
    我们假设$Z^l$到$a^l$有映射函数$\sigma$满足：
$$a_i^l=\sigma (z_i^l)$$
从而建立一竖排z和一竖排a的关系：

    那么整理上面三个式子，可以得到layer与layer的输出关系：

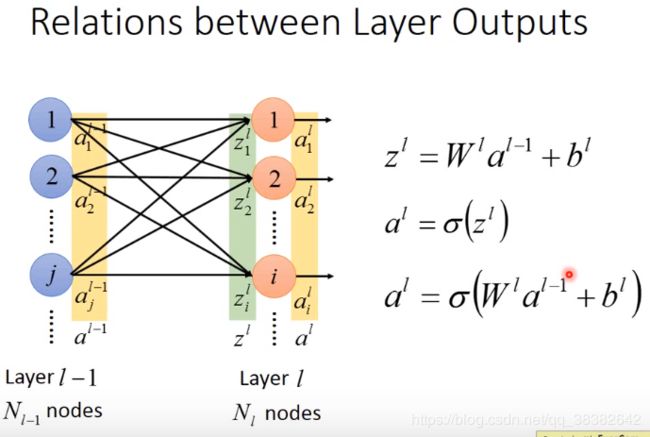
2. Recurrent Structure(RS)

    把同一个structure反复使用就叫RS…
    因为我们需要的不同种类的段并不会因为input的长度而改变，我们需要的参数量永远都是一样的。

1.1 RNN

有一个fcn，输入是两个vector:input:$(h,x)$，输出也是两个vector:KaTeX parse error: Expected group after '^' at position 3: (h^̲',y)。
(图中上标表示one、two),要特别注意设计时$h$和$h^{\prime }$（即图中的$h^0$和$h^1$）它们两个的dimension是一样的，你才能够把他们堆LEGO一样堆到一起。像这样依次类推，新的$f$吃前面一个$f$的output,再产生一个新的$y$.所以只要保证dimension一致，针对MIMO我们只需要同一个$f$就可以产生无限的input/output。

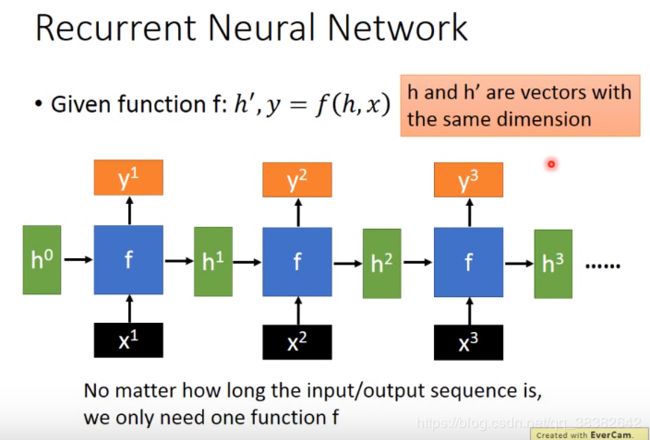
    注：如果我们用feedforward network解这个问题，input x1,x2,x3;output y1,y2,y3.那么当然可以做得到——把x1,x2,x3接起来拼成一个比较长的sequence,再丢到feedforwardnetwork里面，让它吐一个比较长的y1y2y3,但是如果sequence非常长，这时候将x1~x100都拼起来，那这个前馈神经网络它至少在input_layer的地方要很大才能吃的下——参数一多就会导致overfitted(过拟合)
    所以RNN的好处就是便于处理序列，因为它需要很少的参数就能处理这样的问题。

1.2 Deep RNN

    在RNN的基础上，引入一个新的fcn:
$$b^{\prime },c=f_2(b,y)$$
注意f2的输入输出向量的维度与
$$h^{\prime },y=f_1(h,x)$$
向量维度上满足：
$$dimension(h^{\prime })=dimension(h)$$
$$dimension(b^{\prime })=dimension(b)$$
且这里两个函数的$y$是同一个东西

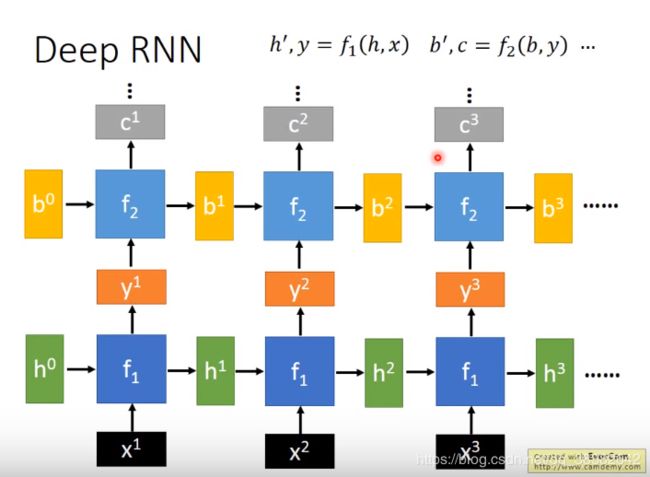
1.3 Bidirectional RNN (双向RNN）

    引入第三个function，$a,c$为$f3$的input vector,$f3$存在的目的就是使得f1与f2的output合在一起.

1.4 Pyramidal RNN (金字塔RNN）

    首先每层塔的白框均代表一个function所形成的MIMO系统，且可以观察到同层的白框两两之间的双向箭头就表示两者相互构成Bidirectional RNN.这是W.Chan用Sequence2Sequence硬做一个语音辨识的网络。因为语音辨识一般是input:Sequence,然后output 一个 character sequence.所以这里就硬train下去，并在paper说这样做真的可以语音辨识。在Paper中提到了一个很重要的trick:让Seq2Seq能做出来的原因
第二层的每个block吃前面一个层的几个layer的好几个output，随着Deep的RNN越来越深，那么迭代得到的Sequence就越来越短。

    但是每一个block运算量变多了，运算量会不会变复杂？其实从平行运算的角度看，一个Seq是没有办法平行运算的，但是一个block却可以实现平行运算。

1.5$f$长什么样子？（以最Naive的RNN为例）

    将输入的$h^{\prime }$和$x$分别乘上对应的weight matrix并相加， 代入sigmoid function中便得到输出$h^{\prime }$.;。如果要得到$y$,同样如图所示。
    r如果$y$是最后的layer，同时希望output是激励的话，可以加一个softmax function.

注：上面的naive就表示一个最简单的RNN。

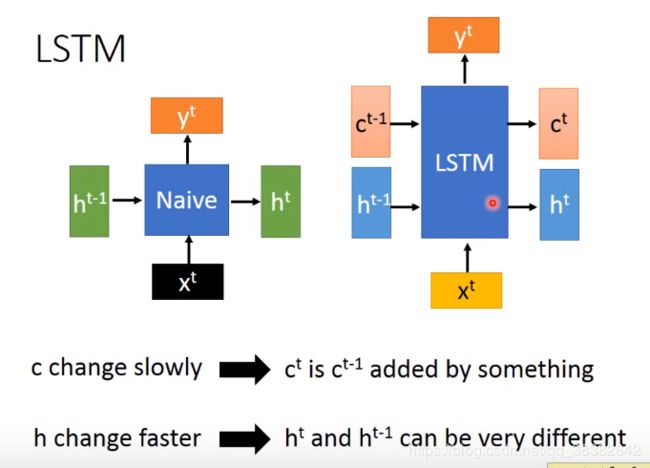
1.6 LSTM (Long Short Term Memory长短时记忆网络)

    如果从block的角度看，LSTM长的和naive的RNN一样，有一个input $x$,然后naive RNN 有一个input$h$,有一个output$h$,这个output$h$就是要去连接其他的RNN的。那么在LSTM里面，它的input有两个要卡死的vector——$c^{t-1}$和$h^{t-1}$，然后output$c^t$和$h^t$去接其他的LSTM.
    总而言之，LSTM比naive RNN多了一个输入向量，从SISO变成了MIMO。
    但区别就在LSTM的c和h扮演了不同的角色。c的变化很慢，$c^{t-1}$加了一些什么（激活函数）才变成$c^t$；从而不同于h vector,这使得c可以记得比较过去的一些info**（慢的c是剧情主线，快的h是每集剧情）**。

1.6.1 LSTM 架构

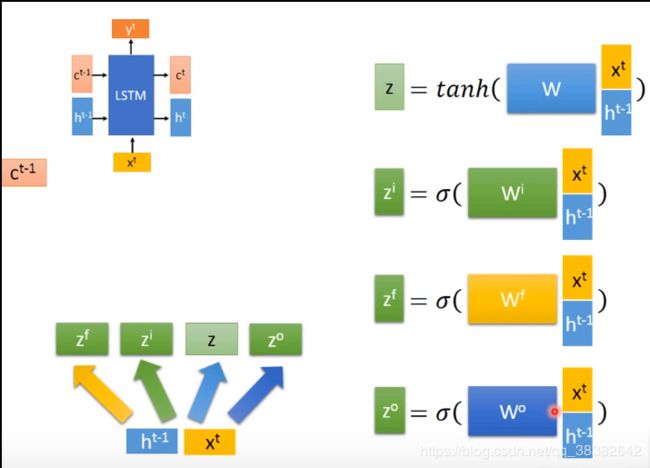
    把x和h并在一起变成一个比较长的vector,再乘上一个weight matrix，再取一个activation function激活函数(如这里的tanh),得到$z$。这里其实可以把$W$拆成$W1，W2$
$$W_1{x}^t+W_2{h}^{t-1}=W(x^t+h^{t-1})$$
    同样地取不同weight matrix和不同的激活函数，可以得到不同的$z^i,z^f,z^o$…从而对同一个vector乘上不同的weight matrix可以得到四个不同的z vector.（四个输入门）
    所以如果能够把四个weight matrix合并成一个打矩阵，就可以四个部分并行计算了。

接下来c有什么作用呢？把c也加入到x和h组成的vector中，这个过程称为peephole
将W分成三部分对应乘x,h,c如下图所示,分别乘对应的weight matrix$W_1$ $W_2$ $W_3$
通常强制乘c的矩阵为diagonal对角矩阵

那么有了这四个vector，接下来我们要做的就是将z与$z^i$相乘，把$c^{t-1}$与$z^f$相乘（向量乘法——对应元素element逐个相乘）
将两部分相乘的结果相加，（这里$z^i$就是input gate,决定z的information能不能留进去，$z^f$就是forget gate，决定$c$的memory能不能够被传到下一个时间点），相加之后就得到下一个时间点的output$c^t$
这里c是细胞状态cell的缩写，f是forget门的缩写
将$c^t$取双曲hyperbolic函数并与$z^o$相乘，得到output$h^t$
最后将$h^t$乘一个matrix再取sigmode function得到$y^t$

接下来将LSTM和RNN一样作为一个block使用，将c,h作为block之间的input/output，element size规则不变…从而得到$c^{t+1}，y^{t+1},h^{t+1}$

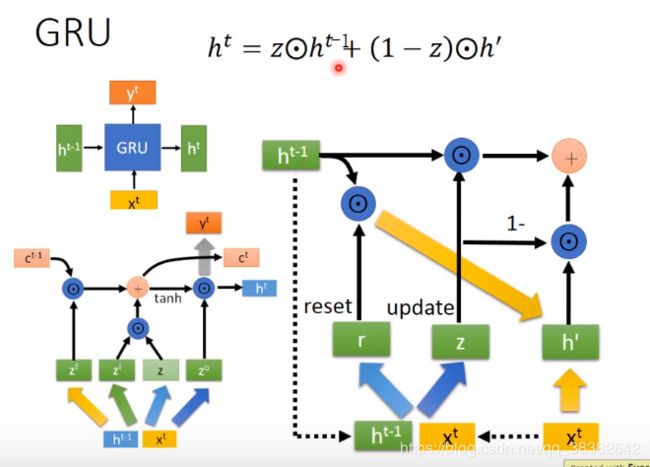
1.7 GRU (Gated Recurrent Unit)

与naive RNN相比GRU的input和output在外观上一样，但是内部与LSTM一样。
把h与x并在一起，再通过weight matrix送入sigmode function得到r（reset gate）
$$r=\sigma (W(h^{t-1}{x}^t))$$
同样更换不同的weight matrix得到$z$

将$r$与$h^{t-1}$并在一起得到的某个vector再与$x^t$这个vector乘第三个matrix得到东西并在一起得到$h^t$

再将两向量$z$与$h^{t-1}$做element wise 相乘得到A
再将$1-z$与$h^t$做element wise 相乘得到B

再A+B,得到$h^t$,再将$h^t$乘上一个matrix(灰色大箭头，这里不同颜色的大箭头表示不同的matrix）得到$y^t$

1.8 GRU与LSTM

LSTM有四个Matrix，GRU有三个Matrix（这块暂时没算上灰色大箭头代表的matrix），所以GRU用的参数比LSTM少，从而不容易overfitted.

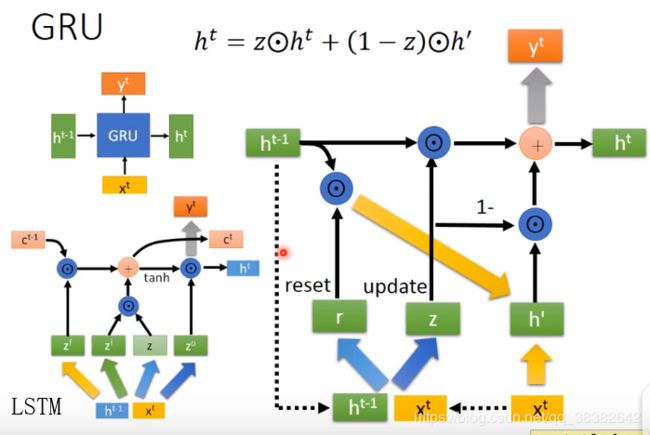
LSTM是先f（忘记），然后再i和z（进行更新cell），然后output进行输出。