计算机图形学实验一(二维图形绘制)
计算机图形学实验一(二维图形绘制)
- 一、实验内容
- 二、实验环境
- 三、问题分析
- 四、算法设计
- 五、源代码
- 六、程序运行结果
一、实验内容
(1)绘制金刚石图案
金刚石图案的成图规则是:把一个圆周等分成n份,然后每两点之间连线。当n取奇数时,该图案可一笔连续绘成,即用MoveTo函数确定一个当前点,然后连续用LineTo函数连点成线。请设计连线规则并编程实现

(2)绘制魔术三角形
绘制下图所示的魔术三角形图案 ,采用三种可明显区分的颜色填充。

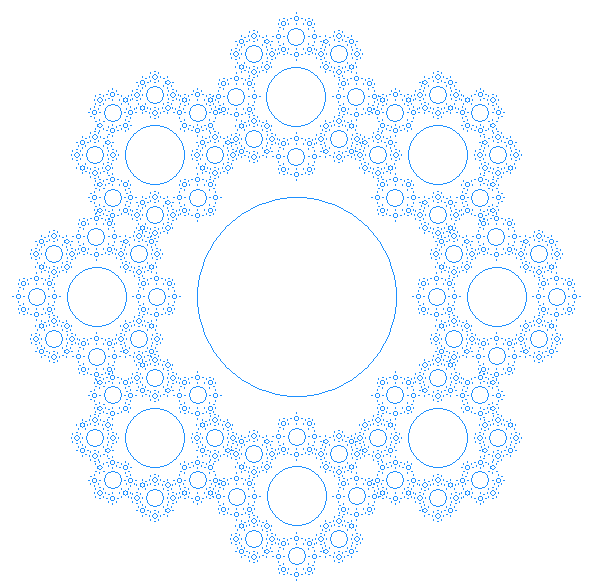
(3)绘制递归圆
应用递归的方法绘制如下所示的图案。

二、实验环境
- 软硬件运行环境:Windows 10
- 开发工具:visual studio 2017
三、问题分析
问题:(1)绘制金刚石图案
- 只有n为奇数时才能一笔画成。
- 主要解决n为奇数的问题,当n为奇数解决后偶数的自然可以画成。
- 主要进行跳跃连接,大致思想为从起始点开始每隔n/2-i(i从1到n/2)个点之间进行依次连接,每个小循环供连接n次,执行n/2个小循环
- 当n/2为n的因子时则需要使跳跃的点+1,这一条线是多画的。
问题:(2)绘制魔术三角 - 先通过六个点确定一个填充图形,三个填充图形可组成一个魔术三角。
- 通过颜色填充和Sleep函数实现颜色逐渐变化的效果。
问题:(3)绘制递归圆 - 主要通过递归函数的调用实现递归圆的绘制
- 递归圆主要在中心点的八个方向上画圆,需要先算出各个圆的位置。
- 再通过递归将每个圆作为新的圆心重新执行第二步。
四、算法设计
(1) 绘制金刚石图案
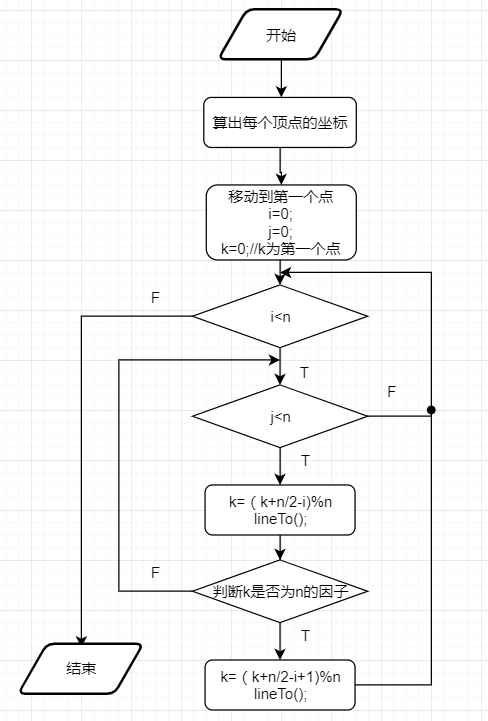
(2) 绘制魔术三角

(3) 绘制递归圆
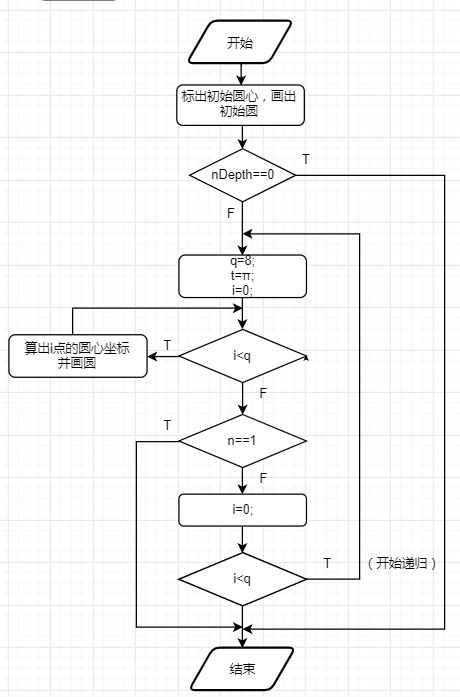
五、源代码
(1)绘制金刚石
//nVertex:顶点数,radius:圆半径,millisecond:笔画之间的延迟时间
void CDiamondView::DrawDiamond(int nVertex, int radius,int millisecond){
InvalidateRect(NULL);//强制清屏
UpdateWindow();
int n=nVertex;
int r=radius;
POINT* pPOINT=new POINT[n];
double x0=600,y0=400;
CDC *pDC = GetDC();
CRect rect(x0-r,y0-r,x0+r,y0+r);
CPen newPen,*oldPen;
newPen.CreatePen(PS_SOLID,1,RGB(0,124,252)); //连线用蓝色
oldPen = pDC->SelectObject(&newPen);
double t;
t=6.28318/n;
for(int i=0;i<n;i++)
{
//算出每个点的坐标
pPOINT[i].x=r*cos(i*t)+x0;
pPOINT[i].y=r*sin(i*t)+y0;
}
int k = 0;//定义第一个点
pDC->MoveTo(pPOINT[k].x,pPOINT[k].y);//移到第一个点处
//画金刚石算法
int firstPoint=k;//记录初始点
for (int i =0; i < n / 2; i++) {
//每隔n/2-i个点开始跳跃,共跳跃n次
for (int j =0; j < n; j++) {
k = (k + n / 2 - i) % n;
pDC->LineTo(pPOINT[k].x, pPOINT[k].y);
Sleep(millisecond);//暂停一会
//判断是不是n的公约数,如果是则连线时连接的间隔点数加一
//因为只有n的公约数才会在没有跳跃n次时回到起点
if (k == firstPoint&j!=n) {
k = (k + n / 2 - i+1) % n;
pDC->LineTo(pPOINT[k].x, pPOINT[k].y);
firstPoint = k;
}
}
}
}
(2)绘制魔术三角
//绘制魔术三角
void CDiamondView::DrawTriangle()
{
InvalidateRect(NULL);//强制清屏
UpdateWindow();
CDC *pDC = GetDC();
int second =1,time=60;
//根据坐标生成魔术三角图案
CBrush newBrush, *oldBrush;
CRgn Rgn1, Rgn2, Rgn3;
POINT vertex1[6] = { {360,116}, {105,555},{512,555},{464,470},{258,470},{460,116} };
Rgn1.CreatePolygonRgn(vertex1, 6, WINDING);
POINT vertex2[6] = { {460,116},{258,470},{362,470},{460,290},{666,644},{718,555} };
Rgn2.CreatePolygonRgn(vertex2, 6, ALTERNATE);
POINT vertex3[6] = { {105,555},{155,644},{666,645},{460,290},{410,380},{512,555} };
Rgn3.CreatePolygonRgn(vertex3, 6, ALTERNATE);
while(time>0){
//第一个填充
newBrush.CreateSolidBrush(RGB(rand()%256,rand()%256,rand()%256)); //生成随机的颜色
pDC->FillRgn(&Rgn1,&newBrush);
Sleep(second*100);
//第二个填充
newBrush.CreateSolidBrush(RGB(rand()%256,rand()%256,rand()%256));
pDC->FillRgn(&Rgn2,&newBrush);
Sleep(second * 100);
//第三个填充
newBrush.CreateSolidBrush(RGB(rand()%256,rand()%256,rand()%256));
pDC->FillRgn(&Rgn3,&newBrush);
Sleep(second * 100);
time--;//直到time为0退出循环
}
}
(3)绘制递归圆
//递归圆的递归函数
void circle(int n,double r, double x0, double y0, CDC *pDC) {
const int q = 8;//周围圆的个数
double t = 6.28318 / q;
double x1[q], y1[q];
for (int i = 0 ; i<q; i++ )
{
x1[i] = 2 * r*cos(i*t) + x0;
y1[i] = 2 * r*sin(i*t) + y0;
CPen newPen, *oldPen;
newPen.CreatePen(PS_SOLID, 1, RGB(30, 144, 255));
oldPen = pDC->SelectObject(&newPen);
CRect rect1( x1[i] - 0.3*r, y1[i] -0.3*r, x1[i] +0.3*r, y1[i] +0.3*r);
pDC->Ellipse(&rect1);
}
if (n == 1) {
return;
}
else {
for (int i = 0; i < q; i++)
{
circle(n-1, 0.3*r,x1[i],y1[i], pDC);
}
}
}
//绘制递归圆主函数
//nDepth:递归深度
void CDiamondView::DrawRecursionCircle(int nDepth)
{
InvalidateRect(NULL);//强制清屏
UpdateWindow();
int x0= 400, y0= 400;//圆心
int r=100;//半径
const int q = 8;//周围圆的个数
int t = 6.28318 / q;
CDC *pDC = GetDC();
CPen newPen,*oldPen;
newPen.CreatePen(PS_SOLID,1,RGB(30,144,255));
oldPen = pDC->SelectObject(&newPen);
CRect rect(y0-r, y0-r, x0 +r, y0 + r);
pDC->Ellipse(&rect);
if (nDepth == 0) {
return;
}
circle(nDepth, r, x0, y0, pDC);
}
六、程序运行结果
(1) 绘制金刚石