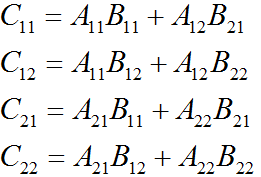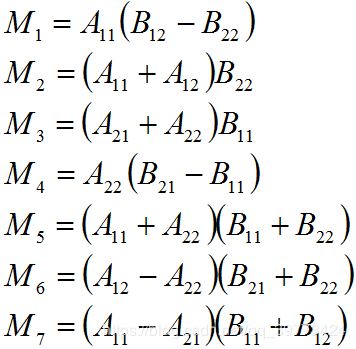算法设计与分析期末复习
1.递归的概念:直接或间接地调用自身的算法称为递归算法,用函数自身给出定义的函数称为递归函数。每个递归函数都要有非递归定义的初始值,如阶乘函数,斐波那契,汉诺塔。
递归函数二要素:边界条件、递归方程
2.分治法的概念:基本思想是将一个规模为n的问题分解为k个规模较小的子问题,这些子问题相互独立且与原问题相同。递归的解这些子问题,然后将各个子问题的解合并得到原问题的解。
(1)如二分法:
函数参数:(a[],x,n)
int left=0,right=n-1;
while(left<=right){
Int middle=(left+right)/2;
if(x==a[middle])return middle;
if(x>a[middle])left=middle+1;
else right=middle-1;
}
return -1;//未找到下标
(2)大整数乘法:无程序,就是减少乘法次数,时间复杂度降低了一点。
每计算出一个C的元素,需要做n次乘法和n-1次加法,n^2个元素时间为O(n^3);
使用分治法:
假设n是2的幂,把矩阵A,B,C都划分成四等份,然后再进行相乘。这样我们只乘了2^2*2=8次乘法,2^2*(2-1)=4次加法。
如果n=2,则可以直接得到最后结果矩阵;如果n>2,则可以继续将子块划分,知道n降到2。——分治降阶的递归算法
然而这样并没有减少乘法次数,时间复杂度木有降低。所以有Strassen改进:
即用7次乘法和若干次加减法就能得到矩阵乘积:
(4)棋盘覆盖:将整个棋盘等分成4份,其中一个特殊方格必在这四个子棋盘中的一个里,其他三个则无特殊方格。所以我们可以用一个L覆盖这三个子棋盘的会合处,这样4个子棋盘就全带有一个特殊方格,化成了同样的问题。递归的将子棋盘都分割,直到棋盘化成了1*1。我们用一个二维数组代表棋盘,设一个全局的整型变量来表示不同的L的编号。
(5)合并排序:将待排序的n个元素分成大小大致相同的两个子集合,分别对两个子集合排序,最终将排好序的子集合合并。
void MergeSort(a[],int left,int right){
if(left
int i=(left+right)/2;
MergeSort(a,left,i);//前半段排序
MergeSort(a,i+1,right);//后半段排序
Merge(a,b,left,i,right);//把前后两次排好的合并到数组b
Copy(a,b,left,right);//复制回数组a
}
时间复杂度O(nlogn)
(6)快速排序
void Qsort(T a[],int p,int r){
if(px);
if(i>j)break;
swap(a[i],a[j]);
}
a[p]=a[j];
a[j]=x;
return j;
} 俩游标分别从子数组的首尾元素开始向中间移动,i的作用是寻找比轴大的元素,然后让其与j替换,j的作用是寻找比轴小的元素,让其与i替换。
3.动态规划
和分治法类似,都是将待求问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。而动态规划的子问题往往是相互不独立的,所以可以用一个表来记录所有子问题的解,以免再之后重复计算。
动态规划基本要素:
「1」最优子结构性质:
当问题的最优解包含了其子问题的最优解时,则称该问题具有最优子结构性质。这个性质是动态规划算法求解的重要线索。
「2」子问题重叠性质
在运用递归算法自顶向下解题时,每次产生的子问题并不总是新问题,动态规划将计算过的子问题保存在一个表格中,当再次使用时直接搜索到它拿过来用就行了。
一般步骤如下:
·找出最优解的性质,刻画其结构特征
·递归的定义最优值
·自底向上,计算出最优值
·根据计算最优值时得到的信息,得出最优解
(1)大矩阵乘法
找出一种最优的乘法次序
普通算法是,A矩阵的第i行各个元素与B矩阵的第i列的各个元素相乘求和,用动态规划,我们可以先假设在第k位置上将矩阵链断开,找到最优解,则问题变成了两个子问题:(AiAi+1……Ak),(Ak+1……Aj)
用m[i][j]表示矩阵i到矩阵j连乘的最优值,那么两个子问题对应的最优值变成m[i][k],m[k+1][j],把这两个加起来,再加上这两大块矩阵(A[i,k]和A[k+1,j])相乘的计算量,即为A[i,j]的最优次序。
设矩阵Am的行数为pm,列数为qm,矩阵是可连乘的,即相邻矩阵qm=pm,所以(AiAi+1……Ak)可表示为pi * qk,
(Ak+1……Aj)可表示为pk* qj,qk = pk.则两个矩阵连乘的乘法次数为Pi * Pk* qj。
得到最优值的递推定义:
m[i][j]=0,i==j
m[i][j]=min(k从i到j-1){m[i][k]+m[k+1][j]+pi-1pkpj}
时间复杂度O(n^3)
(2)最长公共子序列
X{x1,x2...,xm},Y{y1,y2...,yn},设最长子序列为Z={z1,z2,....,zk}
这个问题分三种情况解决,一,当用动态规划解决,若xm=yn,则zk=xm=yn,zk-1是Xm-1和Yn-1的最长子序列;二,当xm!=yn且
xm!=zk,则Z是Xm-1和Yn的最长子序列,三,同二,当xm!=yn且ym!=zk,则Z是Xm和Yn-1的最长子序列。这样就满足了最优子结构性质。
用C[i][j]来记录Xi,Yj的最优子序列的长度,根据上面三种情况,递推公式很容易出来了,不再赘述。
(3)流水作业调度
找出n个作业在2个机器上的最优调度顺序,这和之前的双击调度不同,每个作业需要先后由2台机器合作完成。
流水作业调度的johnson算法:
·令N1={i|ai
·将N1中作业按ai的非递减顺序排列,N2的非递增序列排序。
·N1中作业接N2中作业构成满足johnson法则的最优调度方案。
(4)0-1背包
m(i,j)为背包容量为j,可选物品为i,i+1,i+2,...n时的最优值。对于每一个都有装和不装两种,取两者最大。
m(i,j)=max{m(i+1,j),m(i+1,j-wi)+vi} ,j>=wi
m(i,j)=m(i+1,j), 0<=j
这个问题很典型,不想写了
(5)最优二叉搜索树,时间复杂度O(n^2)
(6)用动态规划算法解决最大字段和问题,其时间复杂性为n
4.贪心算法
贪心算法并不从整体的最优解考虑,而是做出当前的局部最优的选择。两个要素是组优子结构和贪心选择性质,贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择(即贪心选 择)来达到。
(1)活动安排问题
给出了每个活动的起止时间,在所有的活动中找出最大的相容活动子集。
(2)哈夫曼编码
基本思想是,首先所有字符对应n 棵树构成的森林,每棵树只有一个结点,根权为对应字符的频率。然后,重复下列过程n-1 次:
将森林中的根权最小的两棵树进行合并产生一个新树,该新树根的两个子树分别是参与合并的两棵子树,根权为两个子树根权之和。
时间复杂度:O(nlogn)
(3)Prim算法(保证连通,加n-1条边):时间复杂度O(n^2)
(4)Kruskal算法(保证无回路,加n-1条边):时间复杂度:O(nlogn)
动态规划算法与贪心算法的异同:
共同点:
都需要最优子结构性质,
都用来求有优化问题。
不同点:
动态规划:每一步作一个选择——依赖于子问题的解。
贪心方法:每一步作一个选择——不依赖于子问题的解。
动态规划方法的条件:最优子结构性质;子问题的重叠性质。
可用贪心方法的条件:最优子结构性质;贪心选择性质。
动态规划:自底向上求解(动态规划方法是自底向上计算各个子问题的最优解,即先计算子问题的最优解,然后再利用子问题的最优解构造大问题的最优解,因此需要最优子结构)
贪心方法: 自顶向下求解。
可用贪心法时,动态规划方法可能不适用;
可用动态规划方法时,贪心法可能不适用。
5.回溯:
回溯法的基本思想是:为了避免生成那些不可能产生最佳解的问题状态,要不断地利用限界函数来处死那些实际上不可能产生所需解的活结点,以减少问题的计算量。具有限界函数的深度优先生成法称为回溯法。
回溯法的两种解空间树:子集树和排列树;
剪枝函数:用约束函数在扩展结点处剪去不满足约束的子树;用限界函数剪去得不到最优解的子树。
如背包是子集树,售货商是排列树(O(n!))
6.分支限界法:
常见的两种分支限界法:队列式(FIFO)分支限界法--将活结点表组织成一个队列,按照先 进先出(FIFO)原则选取下一个结点为扩展结点;优先队列式分支限界法--将活结点表组织 成一个优先队列,按照规定的优先级选取优先级最高的结点成为当前扩展结点