数据结构5_队列的实现和基本操作

数据结构6_列表的概念与基本操作

队列：

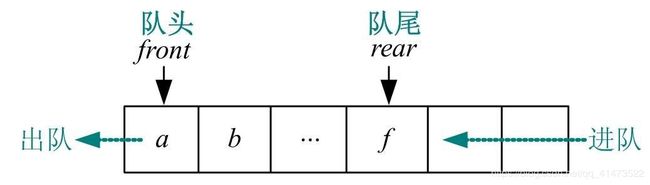
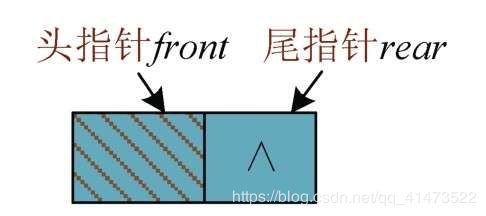
队列是一种先进先出（First In First Out，FIFO）的操作受限的线性表，只能在两端操作，一端只能进叫做队尾（rear），一端只能出叫做队头（front）。和栈相似，队列可以用顺序存储也可以用链式存储；可以把队列想象成一个购票队伍，买完票的总是先离开队列，这也是队列这个称谓的由来；

1. 顺序队列：

顺序队列用一段连续的空间存储数据元素；

1.1 结构体定义：

/*初始化时分配内存*/
typedef struct SqQueue{
	ElemType *base;
	int front,rear;
}SqQueue;
/*定义时分配内存*/
typedef struct SqQueue{
	ElemType data[MaxSize];
	int front,rear;
}SqQueue;

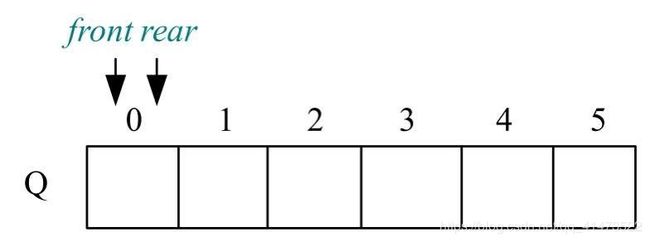
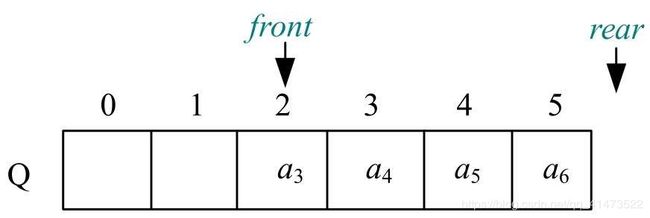
队空状态：Q.front == Q.rear == 0

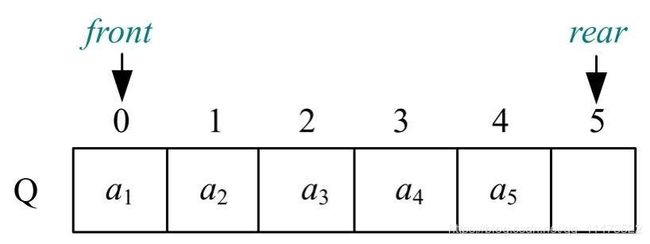
从rear处入队直到队满状态：

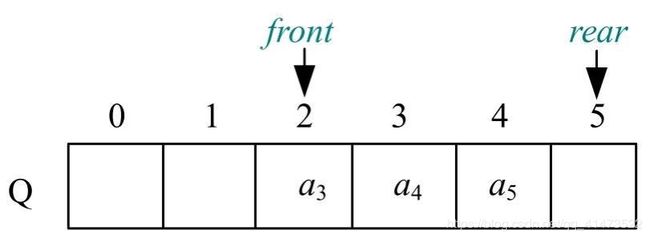
出队操作：

此时在队满状态下再插入元素，Q.rear会超出数组最大下标，但是前面还有两个空间是空的，这种情况称为”假溢出“

---

2 循环队列：

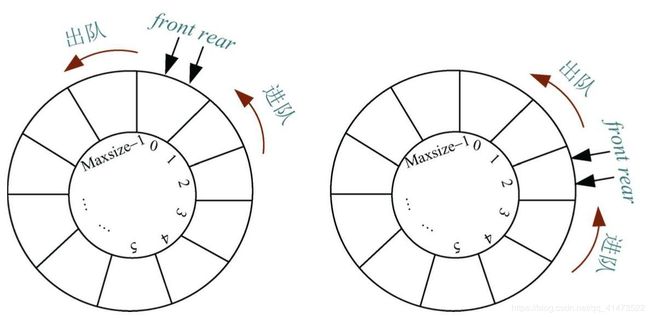
为了解决上述顺序队列出现的问题，这里引入循环队列的概念。将顺序队列臆造成一个环状的空间，即把长长的队列变成首位相衔的环，如下直接上实战：

队空的判定条件：Q.front == Q.rear

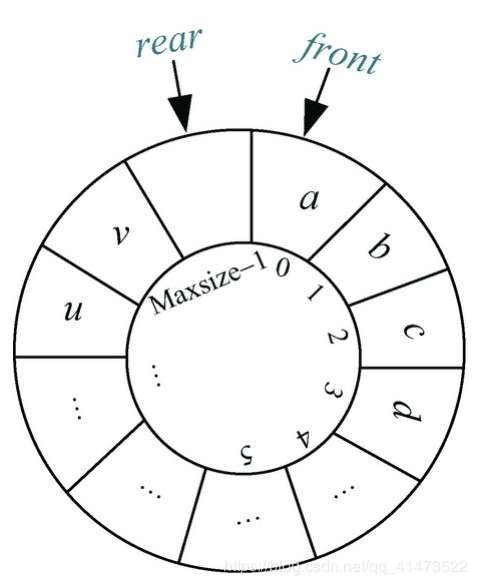
队满的判定条件：通常情况下的方法是牺牲一个空间，当队尾rear指向队头front的下一个位置时，就认为是队满。但是Q.rear向后移动一个位置（Q.rear+1）后，很有可能超过数组的最大下标（即出现data[rear+1]越界），那根据循环首尾相衔的特性这时它的下一个位置应该变为0，如图：

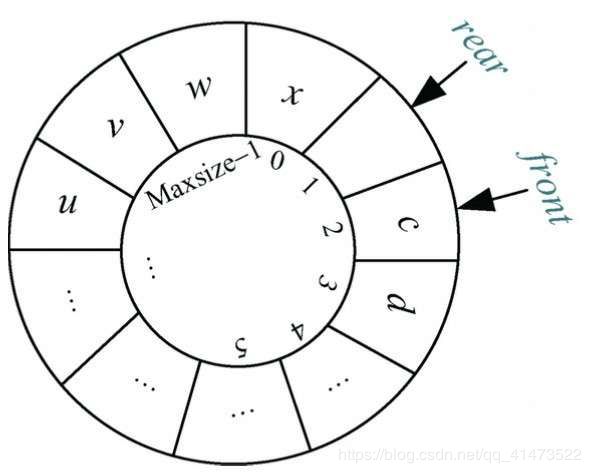
为了保证当Q.rear = MaxSize-1时，Q.rear+1=0，可以考虑取余操作，即（Q.rear+1）%MaxSize=0。而此时（Q.rear+1）%MaxSize = Q.front，此时此式即为队满状态；下图为队满的一般状态，可以和上图对比：

请自行用**（Q.rear+1）%MaxSize == Q.front**此公式判断是否为队满状态；其实，在一般状态下，取余操作也莫得什么用处，只是临界状态下才生效，就是为了保证在临界状态下再增加元素保证数组不会越界；

那此时我们来”臆想“一下入队和出队的操作：

/*入队*/
Q.base[Q.rear] = x;
Q.rear = Q.rear + 1;
/*出队*/
e = Q.base[Q.front];
Q.front = Q.front+1;
/*长度*/
Q.rear-Q.front+MaxSize;

如果此时你一点疑惑都没有，那就给爬，上面写了那么多白写了，爬回去重新看：

下面是才正确的操作：

/*入队*/
Q.base[Q.rear] = x;
Q.rear = (Q.rear + 1)%MaxSize;//非临界状态不需要，但是临界状态下需要”重置“为1
/*出队*/
e = Q.base[Q.front];
Q.front = (Q.front+1)%MaxSize;//同上，当Q.front+1=MaxSize时也需要重置
/*长度*/
(Q.rear-Q.front+MaxSize)%MaxSize;//这个自己比划比划就知道了

2.1 循环队列的基本操作：

2.1.1 循环队列的初始化：

bool InitQueue(SqQueue &Q){
	Q.base = new int[MaxSize];//分配内存
	if(!Q.base) return false;
	Q.front = Q.rear = 0;
	return true;
}

2.1.2 入队：

bool EnQueue(SqQueue &Q, int e){
	if(Q.front = (Q.rear+1)%size) return false;
	Q.base[rear] = e;
	Q.rear = (Q.rear+1)%MaxSize;
    return true;
}

2.1.3 出队：

int DeQueue(SqQueue &Q){
	if(Q.front = Q.rear) return -1;
	int e = Q.base[Q.front];
	Q.front = (Q.front+1)%MaxSize;//不要忘了队头后移
    return e;
}

2.1.4 取队头元素：

int GetHead(SqQueue &Q){
	if(Q.front = Q.rear) return -1;
	int e = Q.base[Q.front];
    return e;
}

2.1.5 求队列长度：

int QueueLength(SqQueue Q){
    return (Q.rear-Q.front+MaxSize)%MaxSize;
}

3. 链队列：

链队列顾名思义就是采用链式存储的队列：

结构体定义：

/*结点定义*/
typedef struct Qnode{//类似于单链表的定义
	ElemType data;
	struct Qnode *next;//指针域
}Qnode,*Qptr;
/*链队列的定义*/
typedef struct{
    Qnode *front;
    Qnode *rear;
}LinkQueue;

3.1 链队列基本操作：

3.1.1 初始化：

链队列的初始化即船舰一个头结点，头尾指针都指向头结点：

voide InitQueue(LinkQueue &Q){
	Q.front = Q.rear = new Qnode;
	Q.front -> next =NUll;
}

3.1.2 入队：

void EnQueue(LinkQueue, int e){
	Qptr s;
	s = new Qnode;
	s -> data = e;
	s -> next = NULL;	
	Q.rear -> next = s;
	Q.rear = s;//这个函数不需要返回bool因为链队列一般不会出现空间满的情况
}

3.1.3 出队：

int DeQueue(LinkQueue &q){
    Qptr p;
    if(Q.front == Q.rear) return -1;  //队空
    p = Q.front->next;  //切记链队列有头指针
    int e = p->data;
    Q.front->next = p->next;  //头指针后移
    if(Q.rear == p) Q.rear = Q.front;  //如果链队列只有一个元素，即此时front->next=rear->next
    delete p;
    return e;
}

3.1.4 取队头元素：

int GetHead(LinkQueue Q){
	if(Q.front!=Q.rear) return Q.front->next->data;
	return -1;
}