C语言实现求取最大公约数的五种算法

第一次上机作业 程序的算法设计
1.题目分析
求最大公约数的算法多以求两个正整数的最大公约数为例加以说明，并且求两个正整数的最大公约数的方法有辗转相除法、穷举法、更相减损法和Stein算法。最大公约数概念如下：如果有一个自然数a能被自然数b整除，则称a为b的倍数，b为a的约数。几个自然数公有的约数，叫做这几个数的公约数。公约数中最大的一个公约数，称为这几个数的最大公约数。
一．辗转相除法（又名欧几里德法）C语言中用于计算两个正整数a,b的最大公约数和最小公倍数，实质它依赖于下面的定理：
a b=0

gcd(a,b) =

gcd(b,a mod b) b!=0
根据这一定理可以采用函数嵌套调用和递归调用形式进行求两个数的最大公约数和最小公倍数,现分别叙述如下：
①函数嵌套调用
其算法过程为： 前提：设两数为a,b设其中a 做被除数,b做除数，temp为余数
1、大数放a中、小数放b中；
2、求a/b的余数；
3、若temp=0则b为最大公约数；
4、如果temp!=0则把b的值给a、temp的值给a；
5、返回第二步；
启示：请注意算法中变量数值之间的相互交换方法、如何取模、怎样进行自定义函数及主调函数与被调函数间的相互关系，函数参数的定义及对应关系特点，利用控制语句如何实现。

②函数递归调用
启示：采用递归调用法要注意递归终止条件的描述，只有找到递归变化的规律，才能有效地解决问题。
二．穷举法（利用数学定义）
穷举法（也叫枚举法）穷举法求两个正整数的最大公约数的解题步骤：从两个数中较小数开始由大到小列举，直到找到公约数立即中断列举，得到的公约数便是最大公约数 。
①定义1：对两个正整数a,b如果能在区间[a,0]或[b,0]内能找到一个整数temp能同时被a和b所整除，则temp即为最大公约数。
②定义2：对两个正整数a,b,如果若干个a之和或b之和能被b所整除或能被a所整除，则该和数即为所求的最小公倍数。
三.更相减损法
更相减损术，是出自《九章算术》的一种求最大公约数的算法，它原本是为约分而设计的，但它适用于任何需要求最大公约数的场合。《九章算术》是中国古代的数学专著，其中的“更相减损术”可以用来求两个数的最大公约数，即“可半者半之，不可半者，副置分母、子之数，以少减多，更相减损，求其等也。以等数约之。”
翻译成现代语言如下：
第一步：任意给定两个正整数；判断它们是否都是偶数。若是，则用2约简；若不是则执行第二步。
第二步：以较大的数减较小的数，接着把所得的差与较小的数比较，并以大数减小数。继续这个操作，直到所得的减数和差相等为止。
则第一步中约掉的若干个2与第二步中等数的乘积就是所求的最大公约数。
其中所说的“等数”，就是最大公约数。求“等数”的办法是“更相减损”法。所以更相减损法也叫等值算法。
四．Stein算法
Stein算法由J. Stein 1961年提出，这个方法也是计算两个数的最大公约数。来研究一下最大公约数的性质，发现有 gcd( kx,ky ) = kgcd( x,y ) 这么一个非常好的性质。试取 k=2，则有 gcd( 2x,2y ) = 2 * gcd( x,y )。很快联想到将两个偶数化小的方法。那么一奇一个偶以及两个奇数的情况如何化小呢？
先来看看一奇一偶的情况： 设有2x和y两个数，其中y为奇数。因为y的所有约数都是奇数，所以 a = gcd( 2x,y ) 是奇数。根据2x是个偶数不难联想到，a应该是x的约数。我们来证明一下：(2x)%a=0，设2x=na，因为a是奇数，2x是偶数，则必有n是偶数。又因为 x=(n/2)*a，所以 x%a=0，即a是x的约数。因为a也是y的约数，所以a是x和y的公约数，有 gcd( 2x,y ) <= gcd( x,y )。因为gcd( x,y )明显是2x和y的公约数，又有gcd( x,y ) <= gcd( 2x,y )，所以 gcd( 2x,y ) = gcd( x,y )。至此，我们得出了一奇一偶时化小的方法。
再来看看两个奇数的情况：设有两个奇数x和y，不妨设x>y，注意到x+y和x-y是两个偶数，则有 gcd( x+y,x-y ) = 2 * gcd( (x+y)/2,(x-y)/2 )，那么 gcd( x,y ) 与 gcd( x+y,x-y ) 以及 gcd( (x+y)/2,(x-y)/2 ) 之间是不是有某种联系呢？为了方便设 m=(x+y)/2 ，n=(x-y)/2 ，容易发现 m+n=x ，m-n=y 。设 a = gcd( m,n )，则 m%a=0,n%a=0 ，所以 (m+n)%a=0，(m-n)%a=0 ，即 x%a=0 ，y%a=0 ，所以a是x和y的公约数，有 gcd( m,n )<= gcd(x,y)。再设 b = gcd( x,y )肯定为奇数，则 x%b=0,y%b=0 ，所以 (x+y)%b=0 ，(x-y)%b=0 ，又因为x+y和x-y都是偶数，跟前面一奇一偶时证明a是x的约数的方法相同，有 ((x+y)/2)%b=0,((x-y)/2)%b=0 ，即 m%b=0 ，n%b=0 ，所以b是m和n的公约数，有 gcd( x,y ) <= gcd( m,n )。所以 gcd( x,y ) = gcd( m,n ) = gcd( (x+y)/2,(x-y)/2 )。
整理一下，对两个正整数 x>y ：
1.均为偶数 gcd( x,y ) =2gcd( x/2,y/2 )；
2.均为奇数 gcd( x,y ) = gcd( (x+y)/2,(x-y)/2 )；
2.x奇y偶 gcd( x,y ) = gcd( x,y/2 )；
3.x偶y奇 gcd( x,y ) = gcd( x/2,y ) 或 gcd( x,y )=gcd( y,x/2 )；
现在已经有了递归式，还需要再找出一个退化情况。注意到 gcd( x,x ) = x ，就用这个。
2.算法构造
绘制出所有算法的流程图以及N-S盒图。








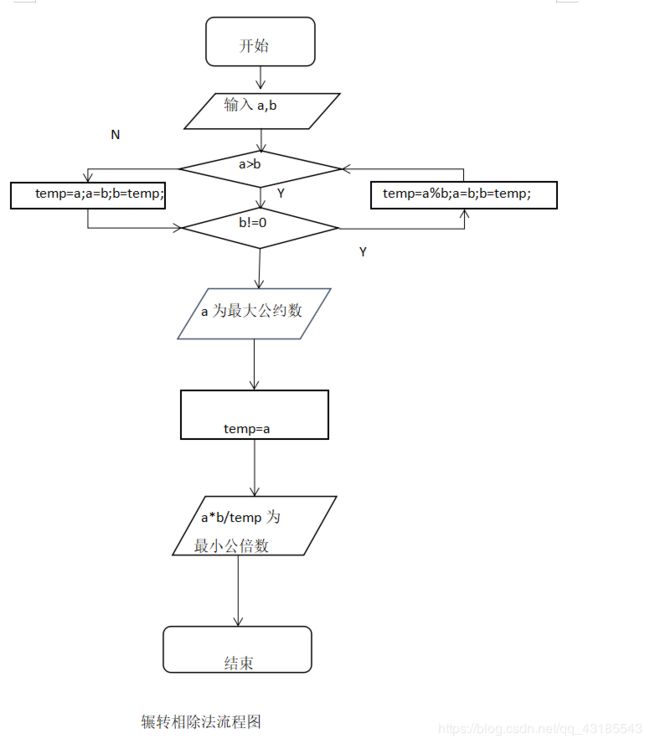
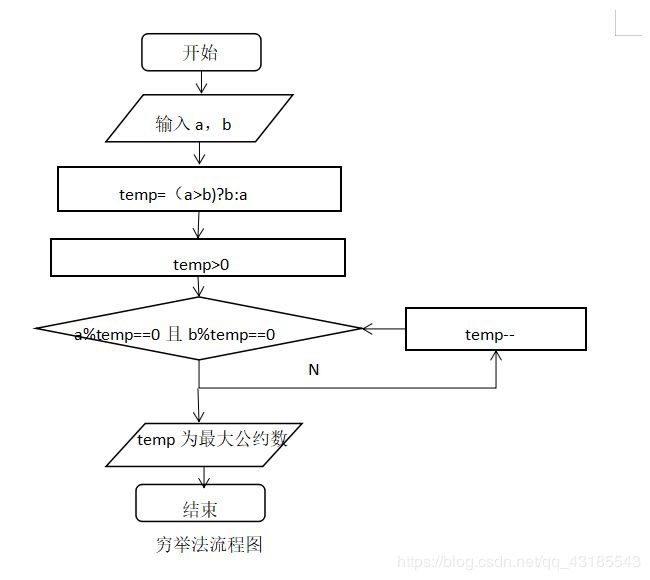
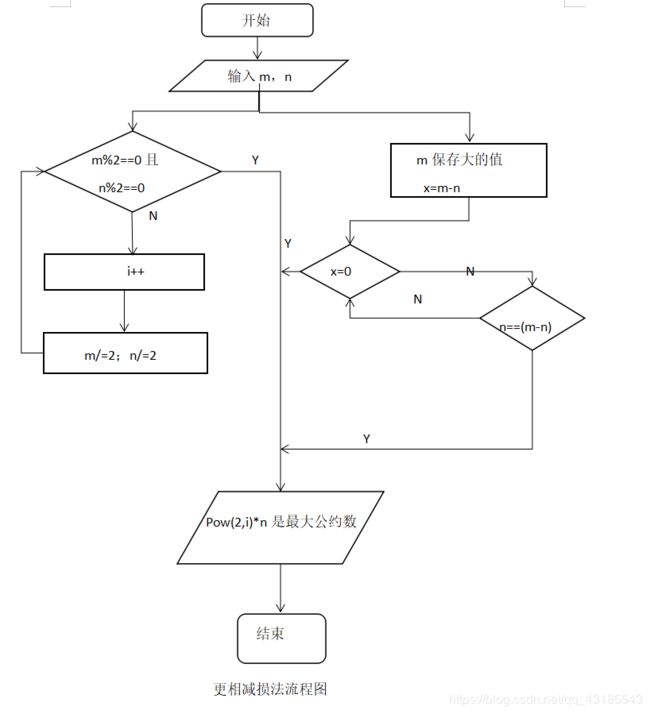
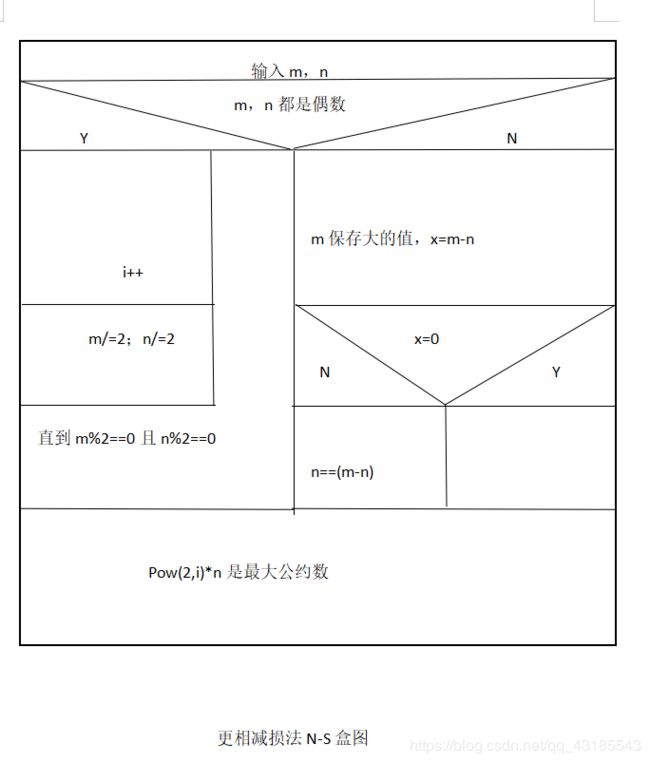
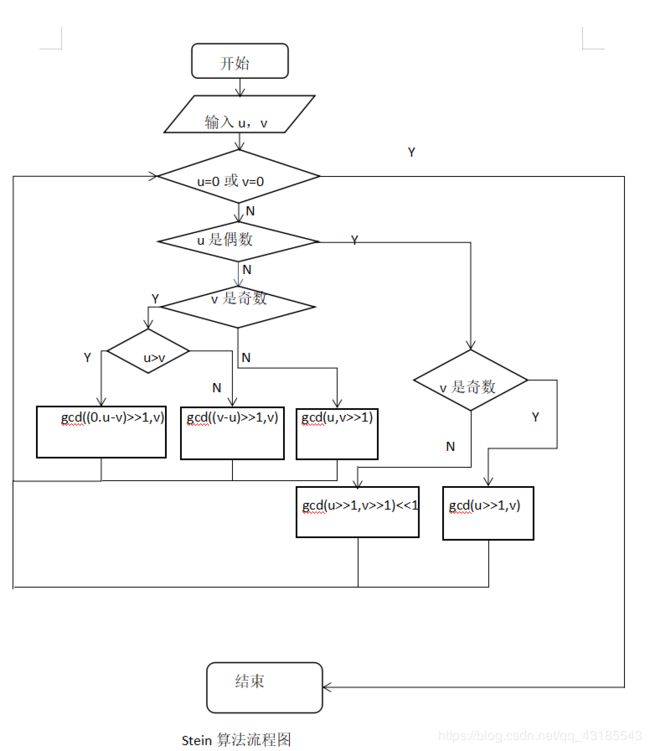
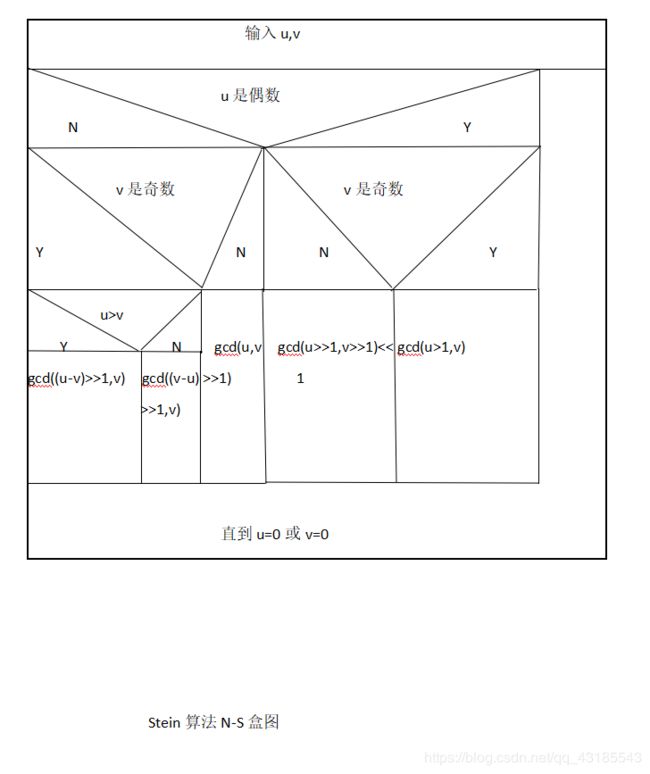
3.算法实现
一、1.辗转相除法中的函数嵌套调用

#include "stdio.h"    /*输入输出类头文件*/
#include 
int divisor (int a,int b)    /*自定义函数求两数的最大公约数*/
{
  int  temp;          /*定义整型变量*/
  if(a<b)             /*通过比较求出两个数中的最大值和最小值*/
    { temp=a;a=b;b=temp;} /*设置中间变量进行两数交换*/
   while(b!=0)           /*通过循环求两数的余数，直到余数为0*/
    {
      temp=a%b;
      a=b;              /*变量数值交换*/
      b=temp;
    }
  return (a);            /*返回最大公约数到调用函数处*/ 
}
int main()  
{
    int z[2][20] = {{1,1},{31,43,46,65,43,58,55,54,55,56,98,78,96,54,78,85,57,12,36,15}};
	int i = 0;
	double run_time;
	LARGE_INTEGER time_start;	//开始时间
	LARGE_INTEGER time_over;	//结束时间
	double dqFreq;		//计时器频率
	LARGE_INTEGER f;	//计时器频率
    int m,n,t1,t2;     /*定义整型变量*/
 QueryPerformanceFrequency(&f);
	dqFreq=(double)f.QuadPart;
	QueryPerformanceCounter(&time_start);	//计时开始
	for( i = 0; i < 20; i++){
		t1 = divisor (z[0][i],z[1][i]);
	printf("The higest common divisor is %d\n",t1);
	}
	QueryPerformanceCounter(&time_over);	//计时结束
	run_time=1000000*(time_over.QuadPart-time_start.QuadPart)/dqFreq;
	//乘以1000000把单位由秒化为微秒，精度为1000 000/（cpu主频）微秒
	printf("\nrun_time：%fus\n",run_time);
	return 0;
}

2.辗转相除法中的函数递归调用

#include "stdio.h"
#include 
int gcd (int a,int b)
{ 
	if(a%b==0)
		return b;
	else
 		return gcd(b,a%b);
  }
int main()
{   
intz[2][20] ={{1,1},{31,43,46,65,43,58,55,54,55,56,98,78,96,54,78,85,57,12,36,15}};
	int i = 0;
	double run_time;
	LARGE_INTEGER time_start;	//开始时间
	LARGE_INTEGER time_over;	//结束时间
	double dqFreq;		//计时器频率
	LARGE_INTEGER f;	//计时器频率
	int m,n,t1;
	getch(); 
   QueryPerformanceFrequency(&f);
	dqFreq=(double)f.QuadPart;
	QueryPerformanceCounter(&time_start);	//计时开始
	for( i = 0; i < 20; i++){
		t1 = gcd(z[0][i],z[1][i]);
		printf("The higest common divisor is %d\n",t1);
	}
	QueryPerformanceCounter(&time_over);	//计时结束
	run_time=1000000*(time_over.QuadPart-time_start.QuadPart)/dqFreq;
	//乘以1000000把单位由秒化为微秒，精度为1000 000/（cpu主频）微秒
	printf("\nrun_time：%fus\n",run_time);
	return 0;
}

二、1.穷举法定义1

#include "stdio.h"
#include 
int divisor (int a,int b) /*自定义函数求两数的最大公约数*/
{
    int  temp;          /*定义义整型变量*/
    temp=(a>b)?b:a;    /*采种条件运算表达式求出两个数中的最小值*/
    while(temp>0)     
    {
       if (a%temp==0&&b%temp==0) /*只要找到一个数能同时被a,b所整除，则中止循环*/
          break;    
       temp--;      /*如不满足if条件则变量自减，直到能被a,b所整除*/
    }
  return (temp); /*返回满足条件的数到主调函数处*/
}
int main()
{  int z[2][20] = {{1,1},{31,43,46,65,43,58,55,54,55,56,98,78,96,54,78,85,57,12,36,15}};
	int i = 0;
	double run_time;
	LARGE_INTEGER time_start;	//开始时间
	LARGE_INTEGER time_over;	//结束时间
	double dqFreq;		//计时器频率
	LARGE_INTEGER f;	//计时器频率
 int m,n,t1;
 getch();
 QueryPerformanceFrequency(&f);
	dqFreq=(double)f.QuadPart;
	QueryPerformanceCounter(&time_start);	//计时开始
	for( i = 0; i < 20; i++){
		t1 = divisor(z[0][i],z[1][i]);
		printf("The higest common divisor is %d\n",t1);
	}
	QueryPerformanceCounter(&time_over);	//计时结束
	run_time=1000000*(time_over.QuadPart-time_start.QuadPart)/dqFreq;
	//乘以1000000把单位由秒化为微秒，精度为1000 000/（cpu主频）微秒
	printf("\nrun_time：%fus\n",run_time);
	return 0;
}

二、2.穷举法中的定义

#include "stdio.h"
#include 
int multiple(int a,int b)
{
  int p,q,temp;
  p=(a>b)?a:b;   /*求两个数中的最大值*/
  q=(a>b)?b:a;  /*求两个数中的最小值*/
  temp=p;      /*最大值赋给p为变量自增作准备*/
  while(1)   /*利用循环语句来求满足条件的数值*/
  {
    if(p%q==0)
      break;  /*只要找到变量的和数能被a或b所整除，则中止循环*/
    p+=temp;   /*如果条件不满足则变量自身相加*/
  }
  return  (p);
}
int main()
{int z[2][20] = {{1,1},{31,43,46,65,43,58,55,54,55,56,98,78,96,54,78,85,57,12,36,15}};
	int i = 0;
	double run_time;
	LARGE_INTEGER time_start;	//开始时间
	LARGE_INTEGER time_over;	//结束时间
	double dqFreq;		//计时器频率
	LARGE_INTEGER f;	//计时器频率
 int m,n,t2;
 getch();
 QueryPerformanceFrequency(&f);
	dqFreq=(double)f.QuadPart;
	QueryPerformanceCounter(&time_start);	//计时开始
		for( i = 0; i < 20; i++){
		t2 = multiple (z[0][i],z[1][i]);
		printf("The lowest common multiple is %d\n", t2);
	}
	QueryPerformanceCounter(&time_over);	//计时结束
	run_time=1000000*(time_over.QuadPart-time_start.QuadPart)/dqFreq;
	//乘以1000000把单位由秒化为微秒，精度为1000 000/（cpu主频）微秒
	printf("\nrun_time：%fus\n",run_time);
	return 0;
}

三、更相减损法

#include "stdio.h"
#include 
#include
int gcd(int m,int n)
{
	int i=0,temp,x;
	while(m%2==0 && n%2==0)  //判断m和n能被多少个2整除
	{
		m/=2;
		n/=2;
		i+=1;
	}
	if(m<n)     //m保存大的值
	{
		temp=m;
		m=n;
		n=temp;
	}
	while(x)
	{
		x=m-n;
		m=(n>x)?n:x;
		n=(n<x)?n:x;
		if(n==(m-n))
			break;
	}
	if(i==0)
		return n;
	else 
		return (int)pow(2,i)*n;
}
int main()
{
	 int z[2][20] = {{1,1},{31,43,46,65,43,58,55,54,55,56,98,78,96,54,78,85,57,12,36,15}};
	int i = 0;
	double run_time;
	LARGE_INTEGER time_start;	//开始时间
	LARGE_INTEGER time_over;	//结束时间
	double dqFreq;		//计时器频率
	LARGE_INTEGER f;	//计时器频率
	int m,n,t1;
 getch();
  QueryPerformanceFrequency(&f);
	dqFreq=(double)f.QuadPart;
	QueryPerformanceCounter(&time_start);	//计时开始
	for( i = 0; i < 20; i++){
		t1 = gcd (z[0][i],z[1][i]);
		printf("The higest common divisor is %d\n",t1);
	}
	QueryPerformanceCounter(&time_over);	//计时结束
	run_time=1000000*(time_over.QuadPart-time_start.QuadPart)/dqFreq;
	//乘以1000000把单位由秒化为微秒，精度为1000 000/（cpu主频）微秒
	printf("\nrun_time：%fus\n",run_time);
	return 0;
} 

四、1.Stein算法函数递归调用

#include "stdio.h"
#include 
int gcd(int u,int v)
{
	if(u==0)	return v;
	if(v==0)	return u;
	if(~u&1)
	{
		if(v&1)
		return gcd(u>>1,v);
		else
		return gcd(u>>1,v>>1)<<1;
	}
	if(~v&1)
		return gcd(u,v>>1);
	if(u>v)
		return gcd((u-v)>>1,v);
	return gcd((v-u)>>1,u);
}
int main()
{
int z[2][20] = {{1,1},{31,43,46,65,43,58,55,54,55,56,98,78,96,54,78,85,57,12,36,15}};
	int i = 0;
	double run_time;
	LARGE_INTEGER time_start;	//开始时间
	LARGE_INTEGER time_over;	//结束时间
	double dqFreq;		//计时器频率
	LARGE_INTEGER f;	//计时器频率
	int m,n,t2;
getch();
  QueryPerformanceFrequency(&f);
	dqFreq=(double)f.QuadPart;
	QueryPerformanceCounter(&time_start);	//计时开始
	for( i = 0; i < 20; i++){
		t2=  gcd(z[0][i],z[1][i]);
		printf("The higest common divisor is %d\n",t2);
	}
	QueryPerformanceCounter(&time_over);	//计时结束
	run_time=1000000*(time_over.QuadPart-time_start.QuadPart)/dqFreq;
	//乘以1000000把单位由秒化为微秒，精度为1000 000/（cpu主频）微秒
	printf("\nrun_time：%fus\n",run_time);
	return 0;
} 

2.Stein算法函数函数非递归调用

#include "stdio.h"
#include 
int Stein(int x,int y)
  /*return the greatest common divisor of x and y*/
{
	int factor=0;
	int temp;
if(x<y)
	{
		temp=x;
		x=y;
		y=temp;
	}
if(0==y)
	{
		return 0;
	}
while(x!=y)
	{
	if(x&0x1)
		{
		if(y&0x1)
		{
			y=(x-y)>>1;
			x-=y;
		}
		else
		{
			y>>=1;
		}
	 } 
else
 {
 	if(y&0x1)
	{
	 	x>>=1;
		if(x<y)
	 	{
	 	temp=x;
	 	x=y;
	 	y=temp;
		}
	}
	else
	{
	 	x>>=1;
		y>>=1;
	 	++factor;
		}	
 	}
	} 
return (x<<factor);
}
int main()
{
	int z[2][20] = {{1,1},{31,43,46,65,43,58,55,54,55,56,98,78,96,54,78,85,57,12,36,15}};
	int i = 0;
	double run_time;
	LARGE_INTEGER time_start;	//开始时间
	LARGE_INTEGER time_over;	//结束时间
	double dqFreq;		//计时器频率
	LARGE_INTEGER f;	//计时器频率
	int m,n,t2;
getch();
  QueryPerformanceFrequency(&f);
	dqFreq=(double)f.QuadPart;
	QueryPerformanceCounter(&time_start);	//计时开始
	for( i = 0; i < 20; i++){
		t2 = Stein(z[0][i],z[1][i]);
		printf("The higest common divisor is %d\n",t2);
	}
	QueryPerformanceCounter(&time_over);	//计时结束
	run_time=1000000*(time_over.QuadPart-time_start.QuadPart)/dqFreq;
	//乘以1000000把单位由秒化为微秒，精度为1000 000/（cpu主频）微秒
	printf("\nrun_time：%fus\n",run_time);
	return 0;
} 

4.调试、测试及运行结果
测试与调试：
先以辗转相除法中函数嵌套调用（版本1）求取最大公约数为例：如图1；

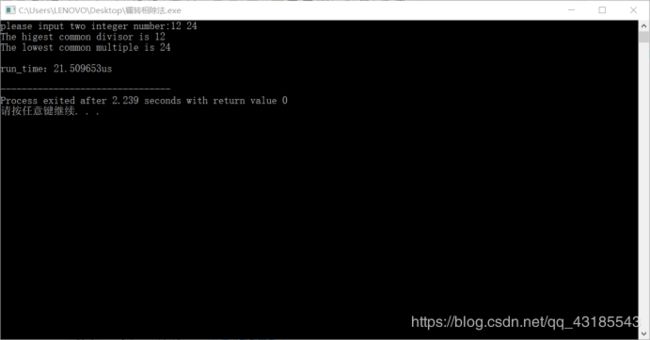
图1：辗转相除法中函数嵌套调用（版本1）求取最大公约数程序运行结果
这个时候，需要人为输入一组数据，来测试程序运行时间较为复杂，如果为提高试验的精确性，需要输入20组数据加以验证则显得极为麻烦，所以采取了便捷省力的方法，那就是引入了二维数组的概念。
再以辗转相除法中函数嵌套调用（版本2）求取最大公约数为例：
这个时候我引入了二维数组，并以加入了20组数据，能方便的得出20组测试数据的情况下的运行时间。如图2；

图2：辗转相除法中函数嵌套调用（版本2）采用20组数据测试，求取最大公约数程序运行结果
附加说明：由于以微秒为单位计时比毫秒计时更为精确，故本实验采用了更为精确的以为妙为单位的计时。
运行结果：
辗转相除法中函数嵌套调用（版本1）求取最大公约数程序运行结果如图3；

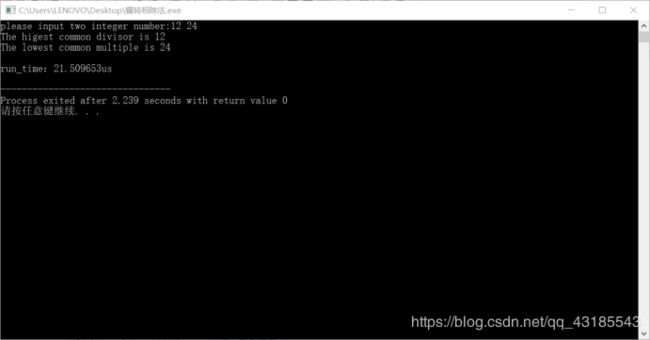
图3：辗转相除法中函数嵌套调用（版本1）求取最大公约数程序运行结果
辗转相除法中函数嵌套调用（版本2）采用20组数据测试，求取最大公约数程序运行结果如图4:；

图4；辗转相除法中函数嵌套调用（版本2）采用20组数据测试，求取最大公约数程序运行结果
辗转相除法中函数递归调用采用20组数据测试，求取最大公约数程序运行结果如图5；

图5：辗转相除法中函数递归调用采用20组数据测试，求取最大公约数程序运行结果

穷举法中采用定义1使用20组数据测试，求取最大公约数程序运行结果如图6；

图6：穷举法中采用定义1使用20组数据测试，求取最大公约数程序运行结果
穷举法中采用定义2求取最小公倍数程序运行结果如图7；

图7：穷举法中采用定义2求取最小公倍数程序运行结果
Stein函数递归调用中采用20组数据测试求取最小公倍数程序运行结果如图8；

图8：Stein函数递归调用中采用20组数据测试求取最小公倍数程序运行结果
Stein函数非递归调用中采用20组数据测试求取最小公倍数程序运行结果如图9；

图9：Stein函数非递归调用中采用20组数据测试求取最小公倍数程序运行结果
5.经验归纳
刚开始做这个实验时，起初使用简单的想法，每次输入一组数据来测试程序运行时间，五种算法输入相同的20组数据。但是，这种想法不仅有悖于程序设计方法学中便捷高效的思想，还为自己增加了计算所造成的负担。因此对程序进行了改编，给五种算法引入二维数组来进行测试程序运行时间。还有，在测试程序运行时间时需要自己查资料，学习如何获取程序运行时间方面的知识，在调用相关方面函数时，一定要记得添加与之相关的头文件。此外辗转相除法中函数递归调用、辗转相除法中函数递归调用、辗转相除法、Stein函数递归调用求取最大公约数及测试程序运行时间没出现问题，但穷举法1及Stein函数非递归调用求取最大公约数在引用20组数据方面出现了问题，即使运行结果体现了利用20组数据测试程序运行时间的效果，但还是存在着不严谨的地方，并没有正确的利用算法获取最大公约数。这也是以后在编程时应注意的问题，更应该思考着解决这些问题的方法、精益求精。
1.注意算法中变量数值之间的相互交换方法、如何取模、怎样进行自定义函数及主调函数与被调函数间的相互关系，函数参数的定义及对应关系特点，利用控制语句如何实现。
2.采用递归调用法要注意递归终止条件的描述，只有找到递归变化的规律，才能有效地解决问题。
3.根据数学定义求任意两个正整数的最大公约数和最小公倍数，相对辗转相除法来说，易懂，容易被接受，但要注意强制退出循环过程的条件、变量的特点及控制语句的使用。
4.欧几里得算法在处理较小数字时优势是明显的，但对于大整数时，高精度的整除和取余运算就显得非常复杂，所以Stein算法的优点就在于只需要进行移位(位运算)和减法操作，处理高精度GCD问题时相对简便。