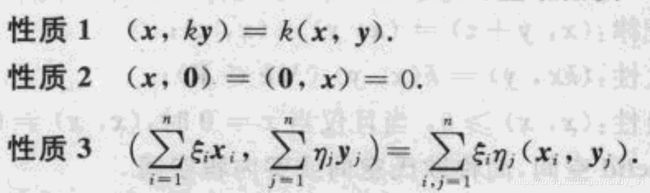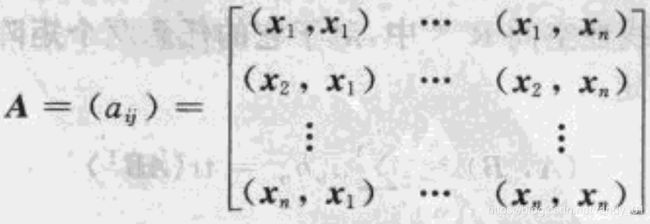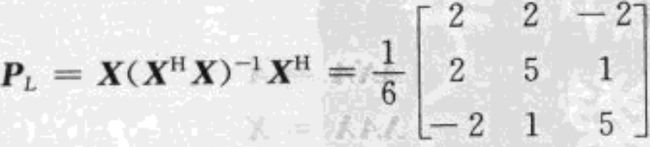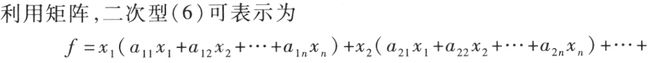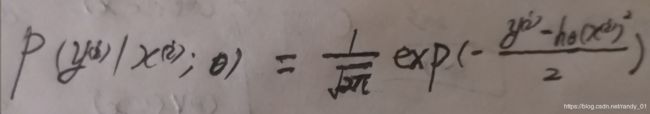探寻《矩阵论》与AI的结合

前言：矩阵论是对线性代数的延伸，很有必要深入研究。矩阵与泛函数分析和凸优化存在着密不可分的关系，尤其是内积空间部分。研究矩阵论可以加深对PCA，SVD,矩阵分解的理解，尤其是第一章入门的线性空间的理解，在知识图谱向量化，self_attention等论文中会涉及大量的矩阵论的知识。本系列博客对此做一个学习心得总结，省略掉矩阵的微分方程等运算部分，重点论述和AI相关尤其是与结构化约束和无向图推理相关的部分。学习一本书的最好方法是看两遍以上，第一遍按顺序学习，第二遍倒着看一遍。比如《矩阵论》的最后一章节关于特殊矩阵的论述，第二遍可以以这个为出发点，重新思考前面的论述，相信会提升很多。从特殊到一般的归纳总结是人类研究自然世界规律的基本方法。关于图模型和深度学习的融合，可以看看DeepMind和谷歌大脑的论文。图模型推理这篇博客地址：https://blog.csdn.net/randy_01/article/details/81743882 联结主义和符号主义的融合是个大难题，但是需要对两个学派有很深入的理解，最起码数学基础应该过硬。目前AI研究的热点大致包括两部分：①Auto ML，包括遗传算法优化神经网络参数等等②逻辑推理，以知识图谱为基础的研究，包括专家规则系统，cvt节点的图谱，kb_qa,神经规则推理。其中优化损失函数是一个重要的研究方向，比如1996年的lasso论文养活了一大批后来的学者。成为研究机器学习专家必须精进以下数学：《矩阵论》+《实变函数与泛函数分析》+《凸优化》+《统计学》，泛函数分析在AI中属于较高级的应用了。建议学习这些学科最好用国外的教材。花费2年左右的时间精研这些数学著作是有必要的，否则会一直停留在应用层面，很被动！有了数学工具，再结合物理学，神经生物学，计算机等学科开展AI研究，将会顺利一些。有人可能不太知道物理学和Ai研究有什么关系，本人认为AI和物理存在着一定的相关性，都是揭示和发现自然世界的规则。AI的研究一定靠规则，尤其是推理。借鉴物理学AI可以更好地发展。目前国内高校的基础研究需要下更大的力度，西湖大学迈出了第一步。目前国内众多高校开设的所谓Ai专业其实是为国家增加人口红利而已，都停留在应用层面，尤其是硕士。后续的博客将会增加物理学和神经生物学基础知识，再后面将介绍AI基础研究的进展，比如胶囊网络提出的原因，神经网络的缺陷，推理的进展，本体论这些。随着研究的深入，本人相信最后一定会进入知识图谱的领域，因为当下只有知识图谱才能真正解决AI的难题。本着一以贯之的原则，本系列文章分成两篇博客论述，并且会对原著进行扩展然后探索在AI中的应用。本系列博客按照以下篇幅展开论述，并且会结合《凸优化》，因为矩阵和《凸优化》紧密相关:

上篇：基础部分

第一部分：矩阵的线性空间，矩阵的意义;

第二部分：矩阵的特征值分解，特征多项式以及矩阵多项式;

第三部分：欧式空间的内积与度量矩阵;

第四部分：矩阵的范数理解与AI应用;

第五部分：矩阵的正交分解理论以及PCA，SVD;

下篇：探索研究与应用，重点在图模型推理部分（图模型和神经网络融合）

第六部分：矩阵的投影理论;

第七部分：矩阵与AI：

       1、矩阵的方法论研究(切入点为特殊矩阵的研究，从特殊到一般的归纳总结是人类研究自然世界的基本规律);

       2、①最小二乘法②对称正定矩阵，矩阵不等式和分类超平面③损失函数的结构化约束④重要的矩阵：拉普拉斯矩阵⑤PageRank⑥无向图的卷积算子（谱卷积算子，相对于图卷积算子）⑦图模型推理.

第5~8部分安排在下篇博客中，这部分既是实际应用又是对第一部分的深化，比如对损失函数结构化约束的深入研究，图模型与联结主义融合的研究等：

第二篇博客地址：https://blog.csdn.net/randy_01/article/details/86618044

在进入正题之前，有必要把《线性代数》里面重要的知识提炼出来：

一、.对称矩阵：①②特征值分解后的特征向量系为标准正交特征向量系

二、可逆矩阵：①②经过行初等变换后可以化简为E。又称为满秩矩阵，非奇异矩阵。

三、正交矩阵：

 

 正交矩阵对一个向量变换成为正交变换，变换后的向量模不变。经典的二次型可以化简为标准二次型，就是对原变量进行正交变换。

四、向量的坐标表示：

 这部分和《傅立叶变换》中傅立叶级数的结果一致，只不过一个是向量空间，一个是函数空间。

 柯西—施瓦茨不等式的证明：构造函数，常量变化量

 有5个不等式很重要，涵盖了统计学，线性代数以及泛函数分析:①柯西-施瓦茨不等式②Jesen不等式③赫尔德不等式④马尔可夫不等式⑤切比雪夫不等式。在赫尔德不等式中，p=q=2时它就是柯西-施瓦茨不等式的上界。在证明指数和的对数函数是凸函数时用到了柯西不等式。

五、矩阵相似性：这部分以特征值分解为基础，精华是方阵A(可逆)与它的特征值对角阵相似的充要条件是A分解后的特征向量系为n个线性无关的向量组。

六、矩阵的秩：①经过初等变换后非0行或者列的个数取最小数②线性无关的列(行)向量个数③分解后特征值非0的个数。

七、方程Ax=b的解x是凸集，证明如下：

 这个方程的解有三种情况：

在实际工程中错在大量的奇异矩阵，这些矩阵的逆矩阵是广义逆矩阵。伪逆指的是矩阵经过svd后取逆运算。

 八、线性无关的几何解释：矩阵和《凸优化》紧密相关，学不精《凸优化》，对矩阵的理解相当于停留在初级阶段，AI理论研究 也不会深入。线性无关的向量组其实就是这些向量不管如何组合，永远不共面，各自线性独立，比如《凸优化》中下面的这个四面体：

v1-v0,v2-v0,v3-v0这三条边各自线性独立，是线性无关的。但是再加上v4-v0的话就不是线性无关的向量组了，因为v4-v0与前三个向量求和后所在的平面共面。

单纯形的定义是由仿射集展开的，它是多面体的特殊形式。

上篇：基础精进

1.线性空间，矩阵的意义

1.1 线性变换

这部分内容是理解矩阵的基础也是最关键的部分。对于线性空间的基本概念不必多解释，都说矩阵的本质是线性变换，这里有必要总结一下。一般而言，矩阵乘以向量后结果仍然是向量，相当于对向量进行了变换。这个过程可以用《实变函数与泛函数分析》很好地解释。矩阵的变换相当于有界线性算子，从函数空间到函数空间的转换。矩阵是一种映射，输入即定义域是空间中的点(函数)，输出也是函数空间。那么矩阵的值域是什么？

某个空间中所有向量经过变换矩阵后形成的向量的集合，通常用R（A）来表示。设A是m*n的矩阵，称其列向量构成的子空间为A的值域空间，R（A），即任意n*1维的向量x,有Ax=b,b是A值域空间中的一个元素，所有的b构成了A的值域空间。A的零空间由所有满足方程Ax=0的x构成,N（A）。

假设你是一个向量，有一个矩阵要来变换你，这个矩阵的值域表示了你将来所有可能的位置。值域的维度也叫做秩（Rank）。值域所在的空间定义为W空间。

矩阵的变换包括方向和幅度，方向指的是坐标轴，幅度一般值向量的特征值。举一个最直观的例子：

比如说下面的一个矩阵：    它其实对应的线性变换是下面的形式：

因为这个矩阵M乘以一个向量(x,y)的结果是：

上面的矩阵是对称的，所以这个变换是一个对x，y轴的方向一个拉伸变换（每一个对角线上的元素将会对一个维度进行拉伸变换，当值>1时，是拉长，当值<1时时缩短），当矩阵不是对称的时候，假如说矩阵是下面的样子： 

它所描述的变换是下面的样子：

下面从最专业的矩阵论理论，具体解释矩阵的本质。前面的变换其实是对向量的左边进行拉伸或者旋转，所以先介绍一下在矩阵论中坐标轴，坐标系和坐标的概念。   

对于线性空间Vn   ，空间的基e1,e2,……是一组非线性相关向量，就是这些向量组成的行列式不为0。空间中的任一向量都可以写成这些基的线性组合，这些组合系数称之为向量的坐标。空间的基对应空间的坐标系，坐标是对应在坐标系中的。那么一个变换矩阵应该如何理解呢？现有空间里的一个向量x,Tx为向量的象，也就是经过变换后的向量。现推导如下：

 

补充：

 

 

 

 证毕！

1.2 矩阵的正定性判断

      1.21 定义

首先半正定矩阵定义为: 其中X 是向量，M 是变换矩阵

我们换一个思路看这个问题，矩阵变换中，MX代表对向量 X进行变换，我们假设变换后的向量为Y，记做Y = MX。于是半正定矩阵可以写成：这个是不是很熟悉呢？ 他是两个向量的内积。同时我们也有公式：

||X||,||Y||代表向量 X,Y的长度，是他们之间的夹角。 于是半正定矩阵意味着, 这下明白了么？正定、半正定矩阵的直觉代表一个向量经过它的变化后的向量与其本身的夹角小于等于90度。

下面从上面推导的过程来理解，考虑矩阵的特征值：若所有特征值均不小于零，则称为半正定。若所有特征值均大于零，则称为正定。

矩阵经过特征值分解后的特征值是一个对角阵，就是原空间某一个基在变换后的空间的长度变化系数，大于0表示方向一致，小于0表示方向相反，每个向量都会经过变换矩阵A的每列系数组合变换，而A经过分解后分为特征值和坐标轴两部分，每个特征值表明了基的自身变换方向与幅度，>0表明同向变换。如果每个特征值都>0的话，由于向量是由空间的基线性组合而成最终导致变换后的向量与原向量同向变化。

       1.22 半正定矩阵的凸集

              1.221 半正定矩阵是凸集，更准确地说是凸椎，请看如下定义：

 半正定矩阵的约束条件：①主对角线元素>=0,由矩阵的特征值分解的行列式可以证明②行列式>=0，因为特征值全部>=0，由任意n阶矩阵与以特征值为主对角线元素的上三角矩阵相似定理可以得出行列式>=0，证毕！

              1.222 半正定矩阵应用举例

              最有说服力的例子莫过于凸函数的二阶条件判断。

二阶导数形成如下的半正定矩阵：

 大众所熟悉的最小二乘法损失函数公式的二阶导函数就是矩阵P：

 这个公式表示的是中心不在原点的椭球。

2.矩阵的特征值分解以及特征多项式和矩阵多项式

矩阵的特征值分解《线性代数》中就有论述，这里重点论述特征多项式以及矩阵多项式。

2.1 特征多项式

 上述多项式方程也可以表述为：，展开后可以知道，和  的系数分别为：

和    。于是我们可以推导出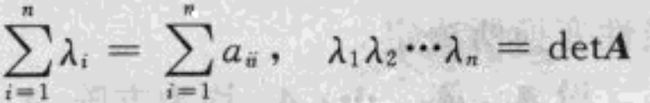。引入记号trA =   ,它是矩阵的迹。上面的公式表明：矩阵A的所有特征值的和等于矩阵的迹，所有特征值的乘积等于detA。

矩阵的特征值分解在《凸优化》中有很重要的应用：

1.

2.

2.2 矩阵的相似性定理

 在《线性代数》中关于矩阵的相似性论述主要集中在矩阵和对角矩阵的相似性。根据定义1.15就可以知道，p为矩阵A的n个线性无关的特征向量系，B为由A的特征值组成的对角阵。再进一步，如果A是n阶对称矩阵，那么p就是标准正交特征向量系。在《矩阵论》中论述更一般的情况:p的组成不全是特征向量系，比如p中可以有一列是特征向量，其余的不是，那么情况是什么呢？论述这样的一般性主要是引出《矩阵论》中最重要的定理：哈密特-凯莱定理(Hamilton-Cayley)。为了证明这个定理，首先引入下面的定理：

 

 

 

 

 为了更进一步消化这个定理，先举个例子：

 

 

 下面引入哈密特-凯莱定理：

 

 

 

 

 从上面的证明过程可以看出，研究矩阵的相似性有多么的重要，为了更进一步研究矩阵的相似性，再来一个例子：设幂级数

的收敛半径为r,如果方阵A满足，则矩阵幂级数是绝对收敛的，如果，则矩阵幂级数是发散的。

分析：在《傅立叶变换》的博客中已经详细讲解了幂级数分解。由证明矩阵幂级数绝对收敛 ，只需证明矩阵幂级数的范数收敛即可，即收敛。 只需证明||A||r，则发散。已知条件谱半径>r，则可以得到对角阵的特征值幂级数是发散的。也就是说只要证明A的特征值幂级数是发散的就可以了。于是我们想到了他的相似三角阵。由于谱半径>r，所以任一特征值均>r，所以特征值幂级数发散，也就是A的相似矩阵幂级数发散，所以A的幂级数发散。证毕！

哈密特-凯莱定理有很多推广和应用，比如：

 

 

 

 下面举个例子：

 

 

3.欧式空间的内积与度量矩阵

欧式空间属于特殊的线性空间，在《实变函数与泛函数分析》的第六章里介绍了Hilbert内积空间。函数可以看作是无限维度的空间向量，比如指数函数的幂级数分解后得到的多项式组合，每个项都可以看作是指数函数的基。所以指数函数(向量)是关于基的线性组合。包括正交三角函数系，也是三角函数的基。重点看一下内积的三个性质：

内积的定义：

 

 内积的性质：

 关于性质3，可以进一步展开：有两个向量X和Y分别关于基x和y线性组合，其中X = ，Y = ，则按照性质3的展开式进一步得到如下：

 

 以上公式表明，只要知道了线性空间中基的矩阵A，就可以得出两个向量的内积。矩阵A成为度量矩阵，可以看出，度量矩阵是对称阵和非奇异矩阵。由于他的对角线上的值全部>0,因此它又是正定矩阵。

度量矩阵的涵义：度量矩阵完全确定了内积，于是可以用任意正定矩阵作为度量矩阵来规定内积。向量所有可度量的量都可以用内积来刻画。

 初中数学中，向量的夹角规定为，是由余弦定理推导出来的。 由于余弦值<=1,所以我们可以得出：

或者。

4.矩阵的范数

4.1向量范数

注意：在《矩阵论》中的范数严格意义上是《实变函数与泛函数分析》中的"半范数"，满足以下3个性质的范数就是半范数。

在本人的博客《实变函数与泛函数分析学习笔记（二）：赋范线性空间》https://blog.csdn.net/randy_01/article/details/82851511

 中有详解介绍。矩阵属于线性代数范畴，几何和代数可以是统一的。下面介绍向量的1阶，2阶和无穷阶范数。

无穷阶范数：

 它是上的  -范数。证明过程很简单，省略掉。这个范数可以扩展到函数，函数可以看作是无限维度的向量，作两个实线性空间的函数，取差值，然后再取差值中的最大值就是无穷阶范数了。

1阶范数：

 它是上的1 -范数，同样省略掉证明，很简单。在深度学习的语义相似度中，利用BiLSTM+self_attention获取到句子对儿语义表示后做差然后取1-范数，用来衡量两个句子的语义差异，称为ma(曼哈顿)距离。最后用exp(-||x1-x2||)作为最后打分函数的映射。事实上exp函数在Ai发挥了十分重要的作用，关于exp函数性质的深入研究，在《傅立叶变换最详细的解读》中有详细讲解。https://blog.csdn.net/randy_01/article/details/83217314

 更形象地解释三种范数：  -范数是PR和RQ中最长的一边，1-范数是PR+RQ，2-范数就是PQ。在一般情况下，ma距离衡量两个句子的语义差异效果更好，可以防止语义丢失问题。

赫尔德不等式是对范数的扩展，在泛函数分析有详细论述。

来看一个精彩的椭圆范数：A是任意n阶对称正定矩阵，x为列向量，则函数

 是x的椭圆范数。

 

在区间[a,b]上定义的实连续函数的集合，构成R上的一个线性空间，可以验证：

 4.2 矩阵范数

设A，定义一个实值函数||A||,他满足以下三个条件：

 由于矩阵有乘法运算，因此再增加一个相容性：

 满足以上4点，称||A||为矩阵A的范数。

下面举例说明几个重要的矩阵范数：

1.已知A=，则存在以下两个范数：

 由于矩阵经常作为向量的空间线性变换(一种映射，规则)出现，因此应该建立矩阵和向量范数的相容性。

定义：对于上的矩阵范数和与上的同类向量范数，如果

 则称矩阵范数 与向量范数 相容。

2.矩阵的Frobenius范数以及AI应用

设A=，则是矩阵的Frobenius范数。

证明过程忽略，有一点需要注意：，则有

即矩阵范数 与向量范数 相容。类似于向量的2-范数，把一个mxn的矩阵看成是碾平的向量，取2-范数即可。

通常所说的矩阵一阶范数指的是列和范数，即取每列绝对值之和最大的数。矩阵的F范数应用是很广的，比如用BiLSTM捕捉到一个句子的embedding，维度为[steps,2u],用最后的压缩向量会丢失很对语义信息，那么构造如下的矩阵A，捕捉到句子的多个维度，最后与H做乘积得到最终的语义表示AH,维度为[c,2u],然后碾平。这个过程的核心就是矩阵的F范数结构化约束，把这个约束加载到损失函数中最为最后的总损失函数。

最后的语义表示为AH，把上面的F范数作为损失函数的结构化约束，得到最后的目标函数。在知识图谱的transD论文里关于entity和relation的相互投影问题以及h和t不在一个空间的问题，可以很好地用矩阵论来解释。

3.矩阵的列和范数，谱范数和行和范数

设A=  ，则从属于向量x的三种范数||x||1,||x||2,||x||的矩阵范数分别为：

 

 

接下来进一步分析谱范数：

 问题转化为凸优化，目标函数是minimize s,约束函数是矩阵不等式(广义不等式)。

5.矩阵的QR分解以及PCA,SVD

矩阵的QR分解理论对PCA和SVD具有非常好的指导意义。矩阵论里面非常好地阐释了QR分解和SVD的关系，这里不做推导了。PCA其实是SVD的外部封装。特征值分解和奇异值分解在机器学习领域都是属于满地可见的方法。两者有着很紧密的关系，特征值分解和奇异值分解的目的都是一样，就是提取出一个矩阵最重要的特征。先谈谈特征值分解吧：

如果说一个向量v是实对称方阵A的特征向量，将一定可以表示成下面的形式： 这时候λ就被称为特征向量v对应的特征值，一个矩阵的一组特征向量是一组正交向量。特征值分解是将一个矩阵分解成下面的形式： 其中Q是这个矩阵A的标准正交特征向量系组成的矩阵，Σ是一个对角阵，每一个对角线上的元素就是一个特征值。这个结论其实是QR分解的一个推广，这个公式更能直观地解释第一部分关于半正定矩阵的解释。我们来看看奇异值分解和PCA的关系吧：

5.1 矩阵的正交对角分解

 

 5.2 矩阵的奇异值分解

上述是《矩阵论》对svd进行的详细解释，但是本人认为还不够。下面结合本人的理解来进一步阐述：

首先来引入《矩阵论》中的初等旋转矩阵和初等反射矩阵。

5.3.初等旋转矩阵

 

 

 

 

 

 初等旋转矩阵是正交矩阵，所以对向量变换时模不变，只是旋转或者是反射。

5.4.初等反射矩阵

 

 

 

 

 

 5.5 用矩阵的svd实现降维

关于PCA降维这里不论述了，重点谈一下利用svd降维的原理。在论述之前，先看以下svd的分解公式：

 

 这个公式很好地阐释了矩阵的线性变换，先是旋转变换，然后中间是拉伸变换，最后再是旋转变换，其中u 和v都是正交矩阵。那么我们可以提取出奇异值的主要值，其余不重要的忽略掉，于是有如下的降维处理：

 5.6 PCA

前面提到了，PCA和SVD本质是一致的，PCA其实是SVD的外部封装。下面直接用最大方差投影理论推导一下PCA。

说明：样本数据矩阵，列代表特征维度，每一行代表一个数据。比如具有两个特征维度的数据集可以表示为（x,y）,那么协方差矩阵就是：[cov(x,x) cov(x,y)

                   cov(y,x) cov(y,y)]

pca降维的一般步骤如下：

①数据预处理，0均值并且归一化

②构建协方差矩阵

③协方差矩阵特征值分解

④对特征值降序排列，找到对应的特征向量系

⑤预处理后的数据集向④中的特征向量系投影

下面用最大方差投影理论解释上述步骤。

构建后的协方差矩阵为n阶Hermite正定矩阵，这意味特征值分解后的特征向量系为标准正交特征向量系，也就是坐标轴。这些坐标轴两辆正交(垂直)，数据集向排序后的部分坐标轴投影，这些投影后的数据具有最大的方差，其余的坐标轴舍弃之。那么投影后的方差和前面步骤中的特征值有何关联？PCA为何要先构建Hermite正定的协方差矩阵？我们从几何角度来看一下：

数据经过预处理后坐标轴是0均值单位向量。现有n个两两垂直的坐标轴，数据集分别向这些坐标轴投影，投影后的数据集仍然为0均值单位向量，那么投影后数据集的方差可以比较大小，从中选出top_r个，这top_r个方差值对应的坐标轴就是我们想要的。

比较PCA和SVD的具体实现过程确实可以肯定，两者本质是一致的。

下篇：

总述：上篇主要论述了矩阵理论的一般性，接下来将进一步深入探讨特殊矩阵以及应用。国外翻译版的《矩阵论》主要教会从业人员一种研究矩阵的方法论。纵观整个篇幅基本可以发现，研究矩阵的方法不外乎以下几种：①feature value decomposition②矩阵相似性~的研究③矩阵分块理论。对矩阵的任何研究都离不开这三种方法，比如奇异值分解，矩阵的分解实际上是相似性和分块理论的融合。矩阵中最重要的元素是feature value,它是矩阵的灵魂。以feature value为核心的研究，包括线性变换，谱范数，feature value估计，矩阵的扰动问题，稳定性等等。矩阵的范数在AI中往往应用在结构化约束中，矩阵的范数还可以证明矩阵的收敛性，最小二乘法损失函数用矩阵可以解释为估计参数满足向量Y在预测值平面内的投影是预测值向量本身。包括在《实变函数与泛函数分析》和《凸优化》中都可以用矩阵来解释，比如泛函数分析中著名的乘积空间其实可以看成是矩阵空间，有界线性算子。《矩阵论》+《实变函数与泛函数分析》+《凸优化》+《统计学》是从事研究工作最基本的数学储备。而普通本科非数学专业的微积分和线代又是前面的基础。但是理论扎实和创新并不是一回事儿，比如国外的Ai研究员可以从生活常识中得到灵感，比如幼儿的抓阄，物理学中的弹簧系统的稳定性等等。建立创新意识比知识储备更重要，也就是增强自身的认知能力，而不只是停留在感知层面。比如有的公司或者研究人员认为扒论文复现很重要，认为本科生做不了。事实上如果中国的教育有质量保证的话，本科生完全可以胜任，因为扒论文复现并不是什么高深和光彩的事儿。

学习学科的目标并不是单纯为了积累知识，方法论才是最重要的。比如国内很多研究生很水，据观察国内很多高校根本不具备开设硕士专业的资格，导师水平不达标,有的甚至不是专业对口的导师，可想而知多么坑人。方法论在知识图谱中以及神经规则推理中更为重要，比如图模型推理的研究，基本思路是融合统计学派和图模型，然后用神经网路学习知识表示。再比如CNN的改进总体离不开以下3种方法：①输入层embedding的扩展，比如融合知识图谱的embedding表示②卷积算子的改进(数学中的卷积算子的研究和有界线性算子很相似)③最后池化层的改进。去年以色列特拉维夫大学和哈弗大学的一篇改进卷积算子(谱卷积算子的论文很不错，很前沿，这些都是工业界最具价值的研究)。目前国内的研究最大的问题是"唯论文论"的浮夸，部分博士不务实，以写论文为生。工业界的进步靠的是少数有价值的论文，而不是论文漫天纷。国内的研究总体上格局不大，有点儿小家子气，保守，习惯于在1的基础上小修小改。从0到1的过程是最具价值的，也是最消耗精力的，需要从基础抓起。比如有的人研究方向很可能不对思路(纯学术派的Ai研究员容易犯这样的错误)，从0到1的研究必须必须慢下来。比如很多工业界的码农学习Ai完全是蜻蜓点水，这是不恰当的，能够评估一篇论文的商业价值需要很强的学术能力和经验。再比如去年微软已经上线的core inferrence chain用cvt节点的图谱做2-hot以上的推理，metapath衡量语义相似度，论文有些人看了以后认为这仅仅是一篇paper而已，草率地认为实际上实现不了。国内确实没有上线的，这说明国内的Ai基础研究明显落后于美国。

1.特殊的矩阵

      1.1 正定矩阵与正稳定矩阵

矩阵的研究方法在总述中已经提到了，看下面的图：

 利用以上结论可以得出：对于n阶Hermite正定矩阵A有，其中P为n阶非奇异矩阵，证明过程用到了第②条结论。这个结论可以直接证明向量的椭圆范数满足三角性。n阶Hermite正定矩阵毫无疑问是稳定的，他是判断线性系统稳定性的重要依据(依据特征值来判断，前面提到矩阵的特征值是矩阵的灵魂)。

      1.2 投影矩阵

1.21 投影算子、投影矩阵和幂等矩阵的概念

 注意：幂等矩阵是A^2=A的矩阵。

 1.22 判断投影矩阵的条件

 1.23 投影矩阵的表示

 举例：

 1.3 正交投影矩阵

 L子空间的向量与M子空间的向量正交，M是L的正交补。

1.31 正交投影矩阵的表示

 x在L上的投影为：

1.32 正交投影矩阵在图模型中的应用

前面的例子不具备很好的说明，现在来论述最速马尔可夫混合链儿问题。在这个例子中，你会很好地看到正交投影矩阵的作用，如何找到矩阵的第二大特征值。

2. 矩阵的一般相似性定理

在第一篇博客已经提到了哈密特-凯莱定理，依据是任意n阶矩阵与三角阵相似。在《线性代数》中论述的是特殊的相似性：n阶非奇异矩阵与对角阵(特征值)相似。更特殊的是n阶对称矩阵的相似性，从特殊到一般的情况是《矩阵论》区别于《线性代数》的地方之一。

二，矩阵与AI

1.最小二乘法的研究

   1.1 椭圆方程

         1.11 标准椭圆方程

               在二维平面内，一个标准的椭圆方程为x^2/a^2 + y^2/b^2 = 1，用矩阵表示为

在《线性代数》的二次型章节中，有标准的二次型矩阵表示，重新回顾一下：

  标准的二次型就是这样的：

 其中C是标准正交特征向量系组成的矩阵。所以以原点为中心的标准椭圆方程就是X^TAX，A为Hermite矩阵，X为椭圆参数。

那么椭圆中心不在原点的方程呢？比如

 很明显此时的方程应该为：(X-X0)^TA(X-X0)

         1.12 旋转后的椭圆方程

                比如将原来的椭圆按原点顺时针旋转thelta度，旋转后的方程是什么样的呢？设原椭圆上的一点a(x1,x2)，旋转后为a`(x1`,x2`)。旋转矩阵为，标记为C，于是a` = Ca。变换一下，将a`逆时针旋转thelta度返回原来的a，此时的旋转矩阵为，替换掉原来的C。于是a = Ca`，带入原来的椭圆方程中得到： （初等旋转矩阵和初等反射矩阵在上一篇博客有论述），中心为X0(x10，x20)的椭圆方程为(X-X0)^T(C^TAC)(X-X0)。

   1.2 最小二乘法损失函数

         1.21 最小二乘法损失函数的由来

                 最小二乘法对于很多AI从业人员来说很熟悉，感觉没什么好说的，但是真要自己独立深入研究就需要功底了。运用数学知识自行研究AI需要方法论指导，首先写出最小二乘法的损失函数公式：

，

线性回归中的样本容量为n,标记Y为真实值，维度为n,Y属于C^n空间，预测值 属于 L(L为C^n的子空间）。

在《统计学》中我们知道，对于回归问题，真实值与预测值之间的误差遵循标准高斯分布，他的概率密度函数为高斯分布函数，因此利用最大似然函数估计得到：

让这个概率密度函数最大化等价于exp()里面的东东最小，于是就有了最小二乘法的损失函数。当然这个只是经验风险估计，还没有加上结构化约束，不能算最后的损失函数，后面将利用《凸优化》论述结构化约束。另外最小二乘法的损失函数属于凸函数，集合属于凸集，可以自己验证一下（两方面可以验证，一是变换成椭球公式，椭球属于典型的凸集，另一种方法求参数的二阶导函数>0）。

         1.22 损失函数的椭圆范数表示

 也就是说X*theltaY沿着M向L的投影，更确切地说是正交投影。我们来验证一下是否正确。公式Y=X*thelta+Z，按照《矩阵论》中投影的定义，Y分解为了两个子空间，这两个子空间直和是完整的C^n空间，所以X*thelta是Y的投影，符合要求。而且是正交投影，那么必有正交投影矩阵P满足以下关系：PY=X*thelta，P为Hermite幂等矩阵。那么至此最小二乘损失函数的意义就是：找到最优的参数thelta使损失函数的椭圆范数最小(最优椭圆)，根据这样的参数thelta能够得到Hermite幂等矩阵P使PY=X*thelta，即X*thelta是Y沿着M(M是L的正交补)的正交投影。X*thelta是对参数thelta的线性变换，把X进行奇异值分解后降维处理或者用PCA降维，X先是对thelta旋转变换，然后伸缩变换，最后再次旋转变换，此时的参数变成了L子空间。在实际工程训练中只能逼近这个理想结论，能否达到主要取决于结构化约束和参数优化方法。于是引出1.23节的论述，请看下文：

         1.23 损失函数的结构化约束(lasso研究)

                 春节后更新……

2.矩阵不等式和分类超平面

      2.1 矩阵不等式

             从最小二乘法的研究过程中可以看出，判断是否为最小二乘的依据就是中间的特征矩阵，如果是n阶Hermite正定矩阵的话，就确定了一个椭球，属于凸集。参数优化过程是找到凸集中的最优椭球参数使损失达到极小值（不是最小值，没有最小值，后面论述区别），也就是使椭球范数局部最小化。接下来讨论对称正定矩阵。

上篇中已经提到正定矩阵的定义，正定矩阵的约束包括：①对角线元素>0②矩阵行列式>0。这里要强调的是，一个对称正定矩阵总是与椭球唯一对应。那么，现有两个点，有多个椭球过这两个点，这里面的最优椭球是哪一个？

-----------------(1)

 这涉及到了矩阵不等式，先谈一下广义不等式。

 广义不等式阐述了锥集中元素的偏序或者几何上的空间位置关系，这在矩阵中体现的更明显。比如上面的y-x指向K的内部，表明用在x的右上方。来看下面的例子：

     2.2 最小与极小元

关于最小与极小元的描述不必太复杂，直接看图：

 

 

3. 重要的矩阵：拉普拉斯矩阵，无向图卷积算子，谱卷积算子，从无向图到有向图的推理研究

    2.1 拉普拉斯矩阵与PageRank算法

    2.2 普通卷积算子，谱卷积算子，无向图推理

          2.21 普通卷积算子

          2.22 谱卷积算子

          2.23 无向图推理

   2.3 从无向图到有向图推理
 

 

后续：最近任正非接受采访时表示，中国的学生基础数学能力连日韩都不如，日本可以提供8k的视频了，但是中国不行，因为数学的问题。认真审视中国的基础教育我们发现，从小学到高中，中国的数学完全停留在低等的感知层面，即解题和刷题。这是数学中最低级的东西，中国却把它奉为圭臬。看看高考的数学考题就可以知道，中国的基础教育没有希望。去年孟晚舟事件后，头条里频繁推荐加拿大和美国的高中数学竞赛题目，中国的很多初中生都会，很多人感觉很简单，于是错误地认为加拿大人的智商没有中国人高。中国人智商确实高，但是很遗憾被基础教育当作机器来训练了，人被成功地降级为了机器。之前总是有人炒作Ai可以取代中国的基础教育，本人很是不认可，但是结合多年研究AI的经验又对比中国的基础教育发现，中国的基础教育和当今的神经网络训练如出一辙：一个数学题经过千百次的练习，相当于深度学习中的归纳偏置，训练过程堪比SGD或者模拟退火或者遗传算法优化神经网络参数，而归纳偏置对应于应试教育的思维定势。中国的基础教育搞成这样，感觉实在是对不起老祖宗，到底是谁的错？奉劝国内的985学生，不要把学历当成镀金的工具，否则实在是对不起985的招牌。中国的基础教育绝对是反人类的，这一点可以得到证明。基础教育改革的突破口在于两点：①高考考题内容②人才评价体系。这两点是教育改革最关键的核心问题，高考考题内容必须改变，向应用建模和探索题靠拢，基础部分要大量减少数学运算和解题，重点考察对数学概念的推导，理解，其他学科也是这个思路。人才评价体系方面，高考考试分数不再是唯一的评价标准，大学是培养人的地方，4年时间应该是节奏很快很累的才对，大学录取面试时重点考察人本身，看看这个人能不能适应大学的生活，看看这个人的价值观，是不是把学历当成镀金的工具等等,不合适的就pass,还有大学4年成绩不到75分以上的不予毕业，而不是刚过60分。探索职业教育与大学教育发展并重，停止错误的扩招，停止教育行政化，推动高校的学术独立，增加985比例……

中国教育改革的突破口在高考改革，高考改革成功了，中国的总体竞争力以及社会都会有所改善。一个国家的社会好不好是由教育决定的，二者可以相互影响。走在一个县城的大街上，如果你发现这个县城的政府大楼和白宫差不多，我们可以断定这个县的基础教育肯定很烂，此处无限循环，break条件目前暂时无解……

马相伯当年在给蔡元培、于右任、蒋梦麟等学生开示时曾说：“大学之大，非大楼之大，应是大师之大”。蒋梦麟在西南联大时期担任北大的校长，力推这个理念。他曾说大学的定位在于搞科研和培养人。如果没有了这两个，大学什么都不是。共产党建立新中国后，大学逐步退化，现在的大学已经沦落为职业培训所，尤其是985高校，实在是耻辱啊，校长下面还有副部级，全球教育界的悲哀和耻辱！目前的教育现状是以抽概率的方式从14亿人中选出"智商高"的人为国家做贡献，保证头部研究，其余的全部牺牲掉。国际上重大的科研成果中国都有，但是整体水平不行，不重视基础教育，只关注几个尖儿， 导致产业整体平均落伍。只有重新回归大学的定位，改变基础教育，均衡发展教育，中国的产业整体才能赶上欧美，光砸钱是没有用的，只能在少数几个关键领域取得突破。