BUAA OO Unit1 表达式求导

第一次作业：幂函数表达式

程序结构

• 读取方式：自动机

• 代码结构：

  • PolyParser：以自动机的方式读取、创建Item
  • Item：记录系数+指数，实现add方法完成化简，实现求导方法
  • PolyItem：使用HashMap记录表达式，键值为指数，实现求导方法

• 复杂度分析

  主要衡量指标：

  • Essentail Complexity (ev(G))：表示一个方法的控制流复杂程度，范围在[1,v(G)]​之间。
  • Design Complexity (iv(G))：表示一个方法调用其他方法的量，范围在[1,v(G)]​之间。
  • Cyclomatic Complexity v(G)：表示方法执行的独立路径数，可以理解为穷尽程序流程每一条路径至少需要的试验次数。
  • Weighted Method Complexity WMC：表示一个类的总循环复杂度

ev(G)	iv(G)	v(G)	WMC

测试

• 自己程序中的Bug：
  • 自动机读取时，由于采用了switch-case遍历状态，导致转换过程较为复杂，在一些情况下出现了数据覆盖的问题。
• Bug检验方法：对拍器
  • 使用Python调用exrex库，根据正则生成表达式；调用Sympy库，完成正确性判定。
  • 使用Java调用Python进程，重定向输入输出流，完成对拍。
  • 由于表达式不含迭代项，代码复杂度不高，状态空间较小，使用随机对拍可有效地解决测试问题。
• 互测方法：对拍+分段提取
  尽量选择简短的对拍错误数据，尝试提取子错误。

对象创建重构

应用PolyParser于简单工厂模式规则：

public class PolyParser {
    ...
    public static String parse(String string){
        PolyParser parser = new PolyParser();
        parser.append(string);
        parser.finish();
        return parser.toString();
    }
}

总结

这次作业中三个类（创建、表达式、项）分配较好，但没有考虑到后续功能扩展的问题，主要精力放在了测试机的搭建方面。在创建类中使用了复杂度较高的自动机，没有使用高级语言的特性简化程序逻辑。

这次作业中出现问题比较多的是读取的层次问题，在第二次作业中得到了较好的解决。

第二次作业：幂函数+三角函数+乘法 表达式

由于第一次作业扩展性过低，因此决定将代码重构，以在基础结构上支持迭代表达式。采用了表达式树的模型，将表达式的所有组成元素抽象为Item，通过引用关系实现表达式树的结构。读取借鉴了递归建立读取表达式树的方法，使用了面向对象的方式实现了递归。

程序结构

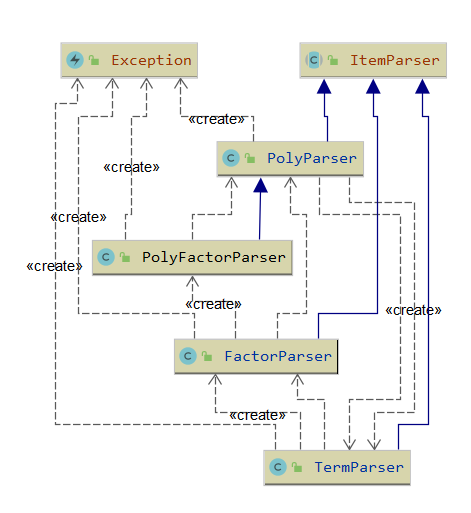
• UML框图

  • Parser部分
    

  • Item部分
    
    ItemMul、ItemSum在化简时调用子表达式的CanMulti/CanAdd接口，尝试进行合并。
    化简策略：尝试使用不同规则变换当前表达式节点，比较输出长度完成化简。每一个表达式节点化简之前先化简下一级表达式节点，递归完成整个表达式的化简。

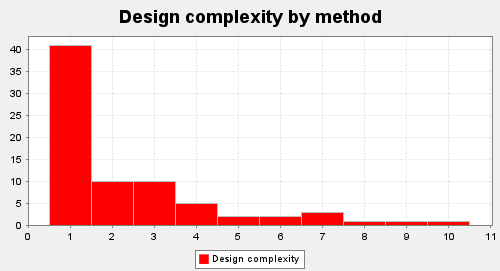
• 复杂度分析
  • 主要方法复杂度出现在化简部分的提取公因子。
  • 由于因子解析器可选项较多，应考虑再创建解析器类。

ev(G)	iv(G)	v(G)

WMC

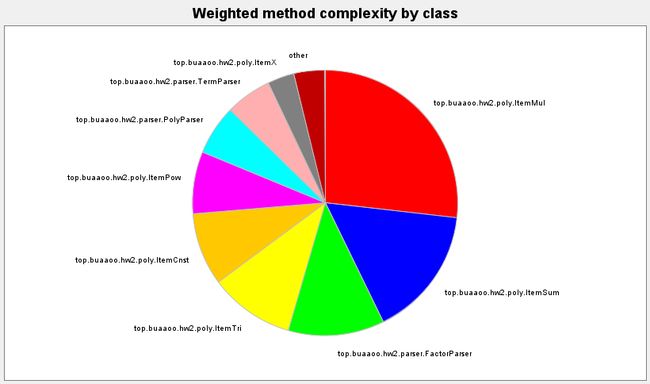• 依赖性分析

  • 主要循环依赖性出现在ItemSum、ItemMul化简/求导时的互相创建，可以通过在Item类中，定义乘法/加法器解决。

  • 另外，由于解析器包的Exception定义为了PolyParser的子类，在抛出异常时产生了循环依赖。

    

测试

和第一次的测试方法相同，对指数范围进行了限定。特别的，由于化简后，Sympy无法直接判定部分恒等式的成立性，采用评测机的方法进行线性随机选取，计算相对误差验证表达式导数正确性。

• 自己程序中的Bug：在三角函数合并的过程中出现了少量的公式错误。应添加更多注释。

第三次作业：多层表达式

在第二次作业的基础上添加了少量修改，以支持输入输出和多层因式分解。

程序结构

• UML框图

  • 添加了PolyFactorParser以支持多层表达式。Item部分和第二次作业相同。
    

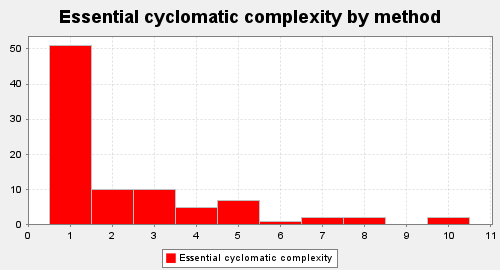
• 复杂度分析

  • 和第二次作业问题类似，但由于表达式迭代问题使公因式化简复杂度进一步上升，将三角函数化简的复杂度转移到了ItemTri类内。

ev(G)	iv(G)	v(G)

WMC

• 依赖性分析

  • 主要循环依赖性出现在ItemSum、ItemMul、ItemTri化简/求导时的互相创建。

  

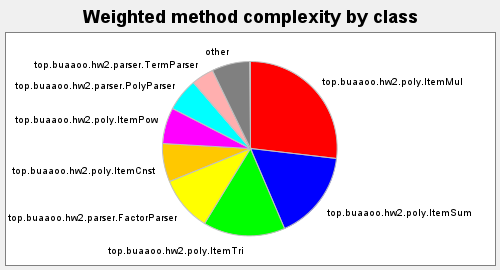测试

由于exrex库不支持递归生成表达式，在正则中只添加了二层表达式。由于导数在化简过程中，公因式合并可能出现多层表达式，因此将上一级的导数输出作为下一级的输入。这种方法同样可以对输出是否符合规则进行对拍。不过由于表达式较为复杂使对拍较慢。由于搜索空间较大使得检索不太全面。

另外，手动添加了多层括号嵌套、多层加法+括号嵌套、多层乘法+括号的嵌套的样例，以解决对拍生成不足的问题。但还是漏掉了0的问题。

• 自己程序中的Bug：
  • 化简迭代问题：化简迭代过程中，一个重要的规则是保证每次递归时，一定是上一层递归的子表达式，否则会出现死递归的情况。然而测试过程中还是出现了少量死递归，原因是加法展开/乘法提取因子时出现了循环。通过定义强制化简策略，强制展开/合并因子，解决了这个问题，同时也增加了搜索空间。
  • 三角函数输出括号问题。这次测试中使sin、cos合并在一个对象中进行了处理，以应用三角恒等变形。然而输出时没有根据表达式的规则，在上一级为sin时在外侧嵌套括号。这个Bug也被遗留到了互测过程中。

对象创建重构

使用抽象工厂模式，定义抽象类ItemParser。PolyParser、TermParser、FactorParser继承ItemParser。

总结

第二次作业中，由于采用了表达式树的架构，在宏观上所有节点都实现了Item，是等效的，没有化简为三元组，在化简三角函数时产生较大的困难。这个应该是由于分布式架构的缺陷导致的效率缺陷，需要增加很多的工作量才能完成集中式架构完成的问题，由于化简不完善，在强测中有2个点几乎没有获得性能分。而在第三次作业中，由于数据结构更为复杂，原来设计的优势被体现出来，在强测中获得了满分。但由于Item类toString函数添加父节点参数后，少修改了一个类，导致互测被hack了一个点。这个也是分布式导致的迭代困难导致的，在修改基类时应仔细考虑。

另外，没有在ItemSum、ItemMul的基础上进一步抽象出带有多个子对象的Item类，导致出现了一些代码重复。如果要兼顾集中性优化与分布式的稳定性，也应该进一步提升程序的层次性。