logistic回归详解
逻辑斯谛回归(logistic regression)是统计学习中的经典分类方法,属于对数线性模型,所以也被称为对数几率回归。这里要注意,虽然带有回归的字眼,但是该模型是一种分类算法,逻辑斯谛回归是一种线性分类器,针对的是线性可分问题。利用logistic回归进行分类的主要思想是:根据现有的数据对分类边界线建立回归公式,以此进行分类。这里的“回归”一词源于最佳拟合,表示要找到最佳拟合参数集,因此,logistic训练分类器时的做法就是寻找最佳拟合参数,使用的是最优化方法,接下来我们都会讲到。
一、Logistic回归函数:
我们先说一个概念,事件的几率(odds),是指该事件发生的概率与该事件不发生的概率的比值。如果事件发生的概率是p,那么该事件的几率是p/(1-p)。取该事件发生几率的对数,定义为该事件的对数几率(log odds)或logit函数: log i t ( p ) = log p 1 − p \log i t(p)=\log \frac{p}{1-p} logit(p)=log1−pp 看了几个博客,我对其取对数的理解大概是这样:事件发生的概率p的取值范围为[0,1],对于这样的输入,计算出来的几率只能是非负的(大家可以自己验证),而通过取对数,便可以将输出转换到整个实数范围内,下面是log函数的在二维坐标系中的图像,依照图像就会对标黄的那句话有一个形象的了解了。
那我们将输出转换到整个实数范围内的目的是什么呢?因为这样,我们就可以将对数几率记为输入特征值的线性表达式 : log i t ( p ( y = 1 ∣ x ) ) = w 0 x 0 + w 1 x 1 + … + w n x n = ∑ i = 0 n w i x i = w T x \log i t(p(y=1 | x))=w_{0} x_{0}+w_{1} x_{1}+\ldots+w_{n} x_{n}=\sum_{i=0}^{n} w_{i} x_{i}=w^{T} x logit(p(y=1∣x))=w0x0+w1x1+…+wnxn=i=0∑nwixi=wTx 其中,p(y =1|x)是条件概率分布,表示当输入为x时,实例被分为1类的概率,依据此概率我们能得到事件发生的对数几率。但是,我们的初衷是做分类器,简单点说就是通过输入特征来判定该实例属于哪一类别或者属于某一类别的概率。所以我们取logit函数的反函数,令 w T x w^{T}x wTx的线性组合为输入,p为输出,经如下推导
log p 1 − p = w T x \log \frac{p}{1-p}=w^{T} x log1−pp=wTx 令 w T x = z 对 上 述 公 式 取 反 令w^{T} x=z 对上述公式取反 令wTx=z 对上述公式取反 则 有 ϕ ( z ) = p = 1 1 + e − z ( 1 ) 则有\phi(z)=p=\frac{1}{1+e^{-z}} (1) 则有ϕ(z)=p=1+e−z1 (1)
公式1就是logistic函数。大家应该对Φ(x)很熟悉,是一个sigmoid函数,类似于阶跃函数的S型生长曲线。

上图给出了sigmoid函数在不同坐标尺度下的两条曲线图。当x为0时,sigmoid函数值为0.5。随着x的增大,对应的sigmoid函数的值将逼近于1;而随着x的减小,sigmoid函数的值将逼近于0。而第二幅图中我们能看到在横坐标的刻度足够大是,在x=0处sigmoid函数看起来很像阶跃函数。
那么对于公式1,我们可以这样解释:为了实现logistic回归分类器,我们可以在每个特征上都乘以一个回归系数,然后把所有的结果值相加,将这个总和带入sigmoid函数中。进而得到一个范围在0-1之间的数值。最后设定一个阈值,在大于阈值时判定为1,否则判定为0。以上便是逻辑斯谛回归算法是思想,公式就是分类器的函数形式。
二、最佳回归系数的确定(极大似然估计+最优化方法)
上一节我们已经确定了logisti分类函数,有了分类函数,我们输入特征向量就可以得出实例属于某个类别的概率。但这里有个问题,权重w(回归系数)我们是不确定的。正如我们想的那样,我们需要求得最佳的回归系数,从而使得分类器尽可能的精确。
如何才能获得最佳的回归系数呢?这里就要用到最优化方法。在很多分类器中,都会将预测值与实际值的误差的平方和作为损失函数(代价函数),通过梯度下降算法求得函数的最小值来确定最佳系数。前面我们提到过某件事情发生的概率为p,在逻辑斯蒂回归中所定义的损失函数就是定义一个似然函数做概率的连乘,数值越大越好,也就是某个样本属于其真实标记样本的概率越大越好。如,一个样本的特征x所对应的标记为1,通过逻辑斯蒂回归模型之后,会给出该样本的标记为1和为-1的概率分别是多少,我们当然希望模型给出该样本属于1的概率越大越好。既然是求最大值,那我们用到的最优化算法就是梯度上升,其实也就是与梯度下降相反而已。
1、我们需要先定义一个最大似然函数L,假定数据集中的每个样本都是独立的,其计算公式如下:
L ( w ) = P ( y ∣ x ; w ) = ∏ i = 1 n P ( y ( i ) ∣ x ( i ) ; w ) = ( ϕ ( z ( i ) ) ) y ( i ) ( 1 − ϕ ( z ( i ) ) ) 1 − y ( i ) L(w)=P(y | x ; w)=\prod_{i=1}^{n} P\left(y^{(i)} | x^{(i)} ; w\right)=\left(\phi\left(z^{(i)}\right)\right)^{y^{(i)}}\left(1-\phi\left(z^{(i)}\right)\right)^{1-y^{(i)}} L(w)=P(y∣x;w)=i=1∏nP(y(i)∣x(i);w)=(ϕ(z(i)))y(i)(1−ϕ(z(i)))1−y(i)
L(w)就是我们以上说的对于损失函数的最原始的定义,但我们还要进一步处理,那就是取对数,在进行极大似然估计的时候我们都知道要取对数,那为什么我们要取对数呢?
首先,在似然函数值非常小的时候,可能出现数值溢出的情况(简单点说就是数值在极小的时候因为无限趋近于0而默认其等于0,具体的可以点解数值移溢出的链接看看这篇博客中的讲解),使用对数函数降低了这种情况发生的可能性。其次,我们可以将各因子的连乘转换为和的形式,利用微积分中的方法,通过加法转换技巧可以更容易地对函数求导。
2、取似然函数的对数:
J ( w ) = log ( L ( w ) ) = ∑ i = 1 n y ( i ) log ( ϕ ( z ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − ϕ ( z ( i ) ) ) J(w)=\log (L(w))=\sum_{i=1}^{n} y^{(i)} \log \left(\phi\left(z^{(i)}\right)\right)+\left(1-y^{(i)}\right) \log \left(1-\phi\left(z^{(i)}\right)\right) J(w)=log(L(w))=i=1∑ny(i)log(ϕ(z(i)))+(1−y(i))log(1−ϕ(z(i)))
这里似然函数是取最大值的,我们可以直接将其确定为损失函数然后使用梯度上升算法求最优的回归系数。但是既然是损失函数,应该还是取最小值好一点,且我们最耳熟能详的方法也是梯度下降,很多书中讲到这里也都是用的梯度下降算法,所以我将以上公式取反来使用梯度下降算法来求最小值(说到底都一样,无非就是取反,一个加一个减)。
J ( w ) = log ( L ( w ) ) = ∑ i = 1 n − y ( i ) log ( ϕ ( z ( i ) ) ) − ( 1 − y ( i ) ) log ( 1 − ϕ ( z ( i ) ) ) J(w)=\log (L(w))=\sum_{i=1}^{n} -y^{(i)} \log \left(\phi\left(z^{(i)}\right)\right)-\left(1-y^{(i)}\right) \log \left(1-\phi\left(z^{(i)}\right)\right) J(w)=log(L(w))=i=1∑n−y(i)log(ϕ(z(i)))−(1−y(i))log(1−ϕ(z(i)))
为了更好地理解这一最终损失函数,先了解一下如何计算单个样本实例的成本:
J ( ϕ ( z ) , y ; w ) = − y log ( ϕ ( z ) ) − ( 1 − y ) log ( 1 − ϕ ( z ) ) J(\phi(z), y ; w)=-y \log (\phi(z))-(1-y) \log (1-\phi(z)) J(ϕ(z),y;w)=−ylog(ϕ(z))−(1−y)log(1−ϕ(z))
通过上述公式发现:如果y=0,则第一项为0;如果y=1,则第二项等于0;
J ( Φ ( z ) , y ; w ) = { − log ( Φ ( z ) ) 若 y = 1 − log ( 1 − Φ ( z ) ) 若 y = 0 J(\Phi(z), y ; w)=\left\{\begin{array}{ll}{-\log (\Phi(z))} & {若\mathrm{y}=1} \\ {-\log (1-\Phi(z))} & {若\mathrm{y}=0}\end{array}\right. J(Φ(z),y;w)={−log(Φ(z))−log(1−Φ(z))若y=1若y=0
下图解释了在不同Φ(z)值时对单一示例样本进行分类的代价:

从上图中可以看到,若y=1,在Φ(z)值越大的情况下,红色的曲线越趋近于0。Φ(z)越大,那么样本被正确划分到1类的概率就越大,这时损失就越小。相对的,Φ(z)越小,意味着样本越有可能属于0类,但是我们知道y=1,在样本属于1类,所以在分类错误的情况下,代价将趋近于无穷。绿线代表着y=0是情况,当然是跟红线相反,我就不多说了。
接下来我们就要使用梯度下降求最小值了。首先,计算对数似然函数对j个权重的偏导:
∂ ∂ w j J ( w ) = ( − y 1 ϕ ( z ) + ( 1 − y ) 1 1 − ϕ ( z ) ) ∂ ∂ w j ϕ ( z ) \frac{\partial}{\partial w_{j}} J(w)=\left(-y \frac{1}{\phi(z)}+(1-y) \frac{1}{1-\phi(z)}\right) \frac{\partial}{\partial w_{j}} \phi(z) ∂wj∂J(w)=(−yϕ(z)1+(1−y)1−ϕ(z)1)∂wj∂ϕ(z)
在进入下一步之前,先计算一下sigmoid函数的偏导:
∂ ∂ w j ϕ ( z ) = ∂ ∂ z 1 1 + e − z = 1 ( 1 + e − z ) 2 e − z = 1 1 + e − z ( 1 − 1 1 + e − z ) = ϕ ( z ) ( 1 − ϕ ( z ) \frac{\partial}{\partial w_{j}} \phi(z)=\frac{\partial}{\partial z} \frac{1}{1+e^{-z}}=\frac{1}{\left(1+e^{-z}\right)^{2}} e^{-z}=\frac{1}{1+e^{-z}}\left(1-\frac{1}{1+e^{-z}}\right)=\phi(z)(1-\phi(z) ∂wj∂ϕ(z)=∂z∂1+e−z1=(1+e−z)21e−z=1+e−z1(1−1+e−z1)=ϕ(z)(1−ϕ(z)
将(2)式带入(1)式中,
( - y 1 ϕ ( z ) + ( 1 − y ) 1 1 − ϕ ( z ) ) ∂ ∂ w j ϕ ( z ) = ( - y 1 ϕ ( z ) + ( 1 − y ) 1 1 − ϕ ( z ) ) ϕ ( z ) ( 1 − ϕ ( z ) ) ∂ ∂ w j z = ( - y ( 1 − ϕ ( z ) ) + ( 1 − y ) ϕ ( z ) ) x j = - ( y − ϕ ( z ) ) x j \begin{array}{l}{ \left(-y \frac{1}{\phi(z)}+(1-y) \frac{1}{1-\phi(z)}\right) \frac{\partial}{\partial w_{j}} \phi(z)} \\ {=\left(-y \frac{1}{\phi(z)}+(1-y) \frac{1}{1-\phi(z)}\right) \phi(z)(1-\phi(z)) \frac{\partial}{\partial w_{j}} z} \\ {=(-y(1-\phi(z))+(1-y) \phi(z)) x_{j}} \\ {=-(y-\phi(z)) x_{j}}\end{array} (-yϕ(z)1+(1−y)1−ϕ(z)1)∂wj∂ϕ(z)=(-yϕ(z)1+(1−y)1−ϕ(z)1)ϕ(z)(1−ϕ(z))∂wj∂z=(-y(1−ϕ(z))+(1−y)ϕ(z))xj=-(y−ϕ(z))xj
我们的目标是求得使损失函数最小化的权重w,所以按梯度下降的方向不断的更新权重:
w j : = w j - η ∑ i = 1 n ( y ( i ) − ϕ ( z ( i ) ) ) x ( i ) w_{j} :=w_{j}-\eta \sum_{i=1}^{n}\left(y^{(i)}-\phi\left(z^{(i)}\right)\right) x^{(i)} wj:=wj-ηi=1∑n(y(i)−ϕ(z(i)))x(i)
由于我们是同时更新所有的权重的,因此可以将更新规则记为:
w : = w - Δ w w :=w-\Delta w w:=w-Δw
其中, Δ w \Delta w Δw定义为: Δ w = η ∇ J ( w ) \Delta w=\eta \nabla J(w) Δw=η∇J(w)
所以综上,我们将梯度下降的更新规则定义为:
Δ w j = − η ∂ J ∂ w j = η ∑ i = 1 n ( y ( i ) − ϕ ( z ( i ) ) x ( i ) ) w : = w + Δ w , Δ w = − η ∇ J ( w ) \begin{aligned} \Delta w_{j} &=-\eta \frac{\partial J}{\partial w_{j}}=\eta \sum_{i=1}^{n}\left(y^{(i)}-\phi\left(z^{(i)}\right) x^{(i)}\right) \\ w & :=w+\Delta w, \Delta w=-\eta \nabla J(w) \end{aligned} Δwjw=−η∂wj∂J=ηi=1∑n(y(i)−ϕ(z(i))x(i)):=w+Δw,Δw=−η∇J(w)
注:如果要用到梯度上升,直接都取反就可以了
三、梯度上升算法(机器学习实战)
在《机器学习实战》一书中有讲到梯度上升法,个人感觉还是挺通俗易懂的,就直接搬过来了。
梯度上升法基于的思想是:要找到某函数的最大值,最好的方法是沿着该函数的梯度方向探寻。如果梯度记为 ∇ \nabla ∇,则函数f(x,y)的梯度由下式表示:
∇ f ( x , y ) = ( ∂ f ( x , y ) ∂ x ∂ f ( x , y ) ∂ y ) \nabla f(x, y)=\left( \begin{array}{c}{\frac{\partial f(x, y)}{\partial x}} \\ {\frac{\partial f(x, y)}{\partial y}}\end{array}\right) ∇f(x,y)=(∂x∂f(x,y)∂y∂f(x,y))
这个梯度意味着要沿x的方向移动 ∂ f ( x , y ) ∂ x \frac{\partial f(x, y)}{\partial x} ∂x∂f(x,y),沿y的方向移动 ∂ f ( x , y ) ∂ y \frac{\partial f(x, y)}{\partial y} ∂y∂f(x,y)。其中,函数f(x,y)必须要在待计算的点上有定义并且可微。一个具体的函数例子见下图。
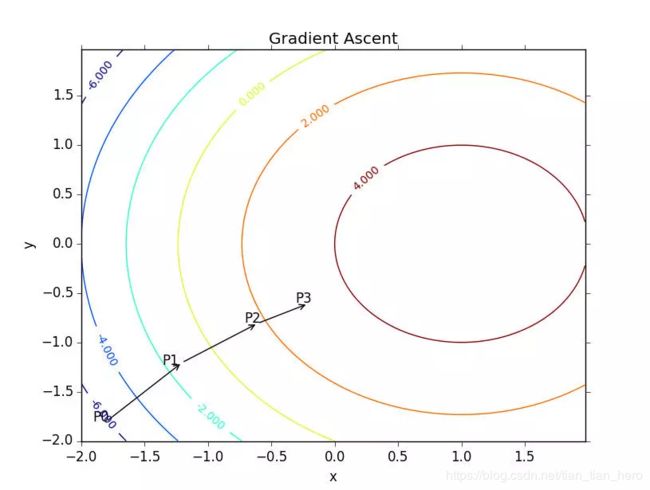
梯度上升算法到达每个点后都会重新估计移动的方向。从P0开始,计算完该点的梯度,函数就根据梯度移动到下一点P1。在P1点,梯度再次被重新计算,并沿新的梯度方向移动到P2.如此循环迭代,知道满足通知条件。迭代的过程中,梯度算子总是保证我们能选取到最佳的移动方向
上图中的梯度上升算法沿梯度方向移动了一步。可以看到,梯度算子总是指向函数值增长最快的方向。这里所说的是移动方向,而未提到移动量的大小。该量值称为步长,记作 α \alpha α。用向量来表示的话,梯度上升算法的迭代公式如下:
w : = w + α ∇ w f ( w ) w :=w+\alpha \nabla_{w} f(w) w:=w+α∇wf(w)
该公式将一直迭代执行,直至达到某个停止条件为止,b比如迭代次数达到某个值或者算法达到某个可以允许的误差范围。
注:如果是梯度下降法,那就是按梯度上升的反方向迭代公式即可,对应的公式如下:
w : = w − α ∇ w f ( w ) w :=w-\alpha \nabla_{w} f(w) w:=w−α∇wf(w)
四、一个简单的算法
下面这个代码也是《机器学习实战》中的,是对以上所讲这些东西的简单实现,用的梯度上升算法,如果大家理解了之前所说的所有的讲解,就很容易看懂程序。
// An highlighted block
from numpy import *
def loadDataSet():
dataMat = [];
labelMat = []
fr = open('testSet.txt')
for line in fr.readlines():
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
labelMat.append(int(lineArr[2]))
return dataMat, labelMat
def sigmoid(inX):
return 1.0 / (1 + exp(-inX))
def gradAscent(dataMatIn, classLabels):
dataMatrix = mat(dataMatIn) # convert to NumPy matrix
labelMat = mat(classLabels).transpose() # convert to NumPy matrix
m, n = shape(dataMatrix)
alpha = 0.001
maxCycles = 500
weights = ones((n, 1))
for k in range(maxCycles): # heavy on matrix operations
h = sigmoid(dataMatrix * weights) # matrix mult
error = (labelMat - h) # vector subtraction
weights = weights + alpha * dataMatrix.transpose() * error # matrix mult
return weights
def plotBestFit(weights):
import matplotlib.pyplot as plt
dataMat, labelMat = loadDataSet()
dataArr = array(dataMat)
n = shape(dataArr)[0]
xcord1 = [];
ycord1 = []
xcord2 = [];
ycord2 = []
for i in range(n):
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i, 1]);
ycord1.append(dataArr[i, 2])
else:
xcord2.append(dataArr[i, 1]);
ycord2.append(dataArr[i, 2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
ax.scatter(xcord2, ycord2, s=30, c='green')
x = arange(-3.0, 3.0, 0.1)
y = (-weights[0] - weights[1] * x) / weights[2] #最佳拟合直线
ax.plot(x, y)
plt.xlabel('X1');
plt.ylabel('X2');
plt.show()
if __name__ =='__main__':
dataArr,labelMat=loadDataSet()
weights=gradAscent(dataArr,labelMat)
plotBestFit(weights.getA())
运行结果:
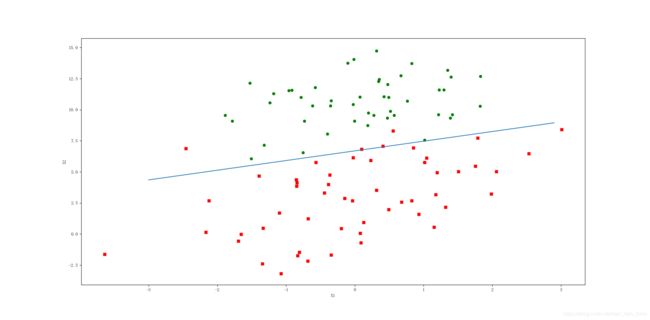
程序中的最佳拟合直线可能大家会有些疑惑,我说一下。这里设置了sigmoid函数中的输入为0,就如我们在最开始的图中所看到的,x=0是两个类的分界线。因此,我们设定 0 = w 0 x 0 + w 1 x 1 + w 2 x 2 0=w_{0} x_{0}+w_{1} x_{1}+w_{2} x_{2} 0=w0x0+w1x1+w2x2,然后解方程得到x1和x2的关系式,即分割线的方程(x0默认等于0)
分类效果还是很不错的,当然这只是一个简单的实现,具体的优化算法等大家可以看一些书籍和博客上都有介绍。本人所了解到的也就这么多,有什么说的不对的地方望见谅,欢迎指正。
参考资料:
1、《机器学习实战》[美]Peter Harrington 著
2、《统计学习方法》 李航 著
3、《机器学习》 周志华 著
4、https://blog.csdn.net/sinat_29957455/article/details/78944939
5、https://blog.csdn.net/gwplovekimi/article/details/80288964#commentBo