红黑树详解
title: 红黑树原理
红黑树提纲
- 2-3树介绍
- 红黑树
该博客都是读者具备二分树基础知识前提下写的(不清楚的不要看下面的内容了,看了也不会明白多少的…)
下面都统一用RBTree表示红黑树。
RBTree很多人都觉得难,其实我刚听到的时候也觉得难。因为大家都说难。。。哈哈~开个玩笑
RBTree其实并没有说的那么难,RBTree是23Tree的变种版本。
所以正常的学习流程应该是先从23Tree学起,然后再去理解红黑树就是一件非常简单的事情了。
RBTree是Robert Sedgewick 这位老哥发明,他老师是唐纳德有兴趣可以搜搜唐纳德是何人。
我这篇博客仅仅只是翻译一点Robert Sedgewick的文档。
这是PDF地址看了这个基本懂了
RedBlack.pdf
红黑树数据结构在线演示
其他数据结构及算法
美团红黑树博客
美团的这篇写的不错,但是我觉得并不是给人看的。讲的那么复杂干嘛。。。。
2-3树介绍
首先需要明白理解23树对于理解红黑树和B树都是有好处。
那么23树是什么?
23树满足二分搜索树的基本性质。
我们看23树的key的种类。
2-node: one key, two children.一个key值,两个儿子节点
3-node: two keys, three children。两个key值,三个儿子节点
当超过3个node的时候会进行树重构,节点上升。
23树的基本定义就是上面这些了。
那么23树的查找怎么做了?
1.比较要查找的key与当前节点中的key值
2.根据key值选择要查找的key所存在的子树区间
3.重复上述步骤(递归实现),直到查找到key
插入的步骤怎么做了?
首先,如果是向一个2-node插入节点的话,那么直接将它转换为3-node就可以了
然后,如果向3-node插入怎么办了?此时已经达到了节点最大值,无法插入数据了。只能做节点变换,一般直接将中间的节点上移到父节点此时就可以插入数据了。
如果不清楚的话先看看上面的PDF中的234树,因为主要讲红黑树
红黑树
这边我要实现的红黑树是一个左倾红黑树,也是相对传统红黑树个人觉得升级的更简洁的红黑树。
首先我们看一下红黑树的定义
1.每个节点或者是黑色,或者是红色。
2.根节点是黑色。
3.每个叶子节点(NIL)是黑色。 [注意:这里叶子节点,是指为空(NIL或NULL)的叶子节点!]
4.如果一个节点是红色的,则它的子节点必须是黑色的。
5.从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点
下面看一张红黑树的实例图(绝对的标准!!!!)
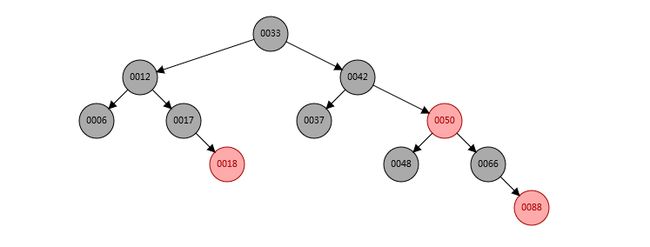
上面的是传统的红黑树而我们要实现的是左倾的红黑树。
与上面仅仅多了一个条件
所有的红色Node都在左边。
看一下具体的实现如下图。
借用一下liuyubobobo波波老师的PPT截了一张图。(懒得画了~哈哈)
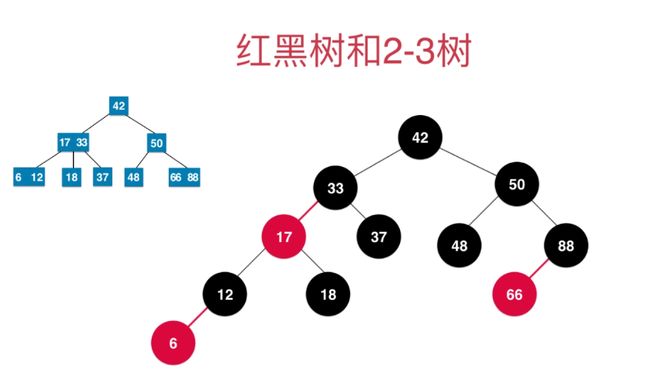
看图肯定觉得传统红黑和左倾里面数据都不一样的位置了。
但是可以保证的是左倾实现代码没有传统复杂并且功能一样,有什么理由拒绝了?
下面咱们自己实现一个红黑树。
首先我参考了Doug Lea的代码也参考了Robert Sedgewick顺带的也参考了bobo老师的代码
bobo老师参考的Robert Sedgewick
他们三个人实现了还是有些细节区别。
比如Robert Sedgewick和bobo都喜欢用递归。
Doug Lea喜欢用死循环。
这些都是有原因的,个人还是觉得Doug Lea更偏向于生产代码。
比较递归层次多一点就stackoverflow了,不过递归也有好处代码简洁写起来也简单。
所以我的代码循环和递归都会用~
我想了一下我还是在代码里面添加注释的方式讲解好了。
/**
* @ClassName LRBTree
* @Description ToDo
* @Author Allen
* @Date 2018/12/16 3:01
* @Version
*/
public class LRBTree<K extends Comparable <K>, V> {
private final RBTreeBase <K, V> rbTree;
abstract static class RBTreeBase<K extends Comparable <K>, V> {
//红黑常量
private static final boolean RED = true;
private static final boolean BLACK = false;
private Node <K, V> root;
private int size;
RBTreeBase() {
root = null;
size = 0;
}
V get(K key) {
Node <K, V> node = findNode(key);
return node == null ? null : node.value;
}
void put(K key, V value) {
Node <K, V> node = addNode(getRoot(), key, value);
setRoot(node);//因为默认添加的元素都是红色,当root元素的时候需要颜色翻转为黑
}
abstract Node <K, V> findNode(K key);
abstract Node <K, V> addNode(Node <K, V> node, K key, V value);
abstract V delete();
protected int getSize() {
return size;
}
protected int setSize() {
return size++;
}
protected boolean isEmpty() {
return size == 0;
}
protected Node <K, V> getRoot() {
return root;
}
protected void setRoot(Node node) {
root = node;
root.color = BLACK;
}
// 判断节点node的颜色
protected boolean isRed(Node node) {
if (node == null)
return BLACK;
return node.color;
}
// node x
// / \ 左旋转 / \
// T1 x ---------> node T3
// / \ / \
// T2 T3 T1 T2
protected Node leftRotate(Node node) {
Node x = node.right;
// 左旋转
node.right = x.left;
x.left = node;
x.color = node.color;
node.color = RED;
return x;
}
// node x
// / \ 右旋转 / \
// x T2 -------> y node
// / \ / \
// y T1 T1 T2
protected Node rightRotate(Node node) {
Node x = node.left;
// 右旋转
node.left = x.right;
x.right = node;
x.color = node.color;
node.color = RED;
return x;
}
// 颜色翻转
protected void flipColors(Node node) {
node.color = RED;
node.left.color = BLACK;
node.right.color = BLACK;
}
//基础节点,通过左右关联
class Node<K extends Comparable <K>, V> {
public K key;
public V value;
public Node left, right;
public boolean color;
public Node(K key, V value) {
this.key = key;
this.value = value;
left = null;
right = null;
color = RED;//默认添加的节点都为红,你也可以默认都为黑。
}
}
}
//遍历的方式
static final class Traverse<K extends Comparable <K>, V> extends RBTreeBase <K, V> {
Traverse() {
super();
}
Node <K, V> findNode(K key) {
Node <K, V> x = getRoot();
while (x != null) {//Doug Lea写会直接一个for死循环,比如这段代码 for (Node e = first; e != null; ) 就是大师的find方法
int cmp = key.compareTo(x.key);
if (cmp == 0) {//相等则就是当前节点
return x;
} else if (cmp < 0) {//小于0说明值比当前节点小,往左边遍历下去
x = x.left;
} else {//大于0说明值比当前节点大,往右边遍历下去
x = x.right;
}
}
return null;
}
/*
* 树重构的时候用到的逻辑
* 用来获取添加节点的parent节点
* 这段代码其实没有存在的必要在NODE类里面添加一个parent字段就可以了
* 但是我这代码是递归和遍历都一起实现
* 为了简单一点就去掉了parent*/
Node <K, V> parentOf(Node <K, V> node) {
Node <K, V> x = getRoot();
K key = node.key;
while (x != null) {
int cmp = key.compareTo(x.key);
if (cmp < 0) {//小于0说明值比当前节点小,往左边遍历下去
if (x.left == node) {
return x;
} else {
x = x.left;
}
} else {//大于0说明值比当前节点大,往右边遍历下去
if (x.right == node) {
return x;
} else {
x = x.right;
}
}
}
return getRoot();//就只有一个root节点
}
@Override
Node <K, V> addNode(Node <K, V> node, K key, V value) {
Node <K, V> root = node;
Node <K, V> parent = null;
if (node == null) {
setSize();
return new Node(key, value); // 默认插入红色节点
}
while (node != null) {//先来一个添加元素,按照二分查找树的方式添加进去
int cmp = key.compareTo(node.key);
if (cmp == 0) {
node.value = value;
return node;
} else if (cmp < 0) {
if (node.left == null) {
node.left = new Node(key, value);
setSize();
break;
} else {
node = node.left;
}
} else {
if (node.right == null) {
node.right = new Node(key, value);
setSize();
break;
} else {
node = node.right;
}
}
}
/*上面按照二分查找树的方式将数据添加进去了,但是咱们的是红黑树所以还需要转换
*当出现树结构重构的时候只有上升节点遇到黑色节点才可以停下来,所以while条件里面只要parent还是红黑
* 就会一直循环下去重构树结构
* */
while ((parent = node) != null && isRed(parent)) {
if (isRed(node.right) && !isRed(node.left)) {//当右侧是红色则左旋转,因为咱们是左倾不可能存在右红
node = leftRotate(node);
}
/*当左侧为红色并且左节点的子节点也为红色则需要又旋转
* 根据23树的右侧为红其实已经是一个3node状态了,没法再加入一个节点
* 所以只会暂时的添加进去,然后进行树重构
* 这时候就需要右侧旋转*/
if (isRed(node.left) && isRed(node.left.left)) {
node = rightRotate(node);
}
/*全部都是红色很明显嘛,全部节点换色*/
if (isRed(node.left) && isRed(node.right)) {
flipColors(node);
}
//继续遍历上去
node = parentOf(node);//这个获取Parent的方法没写好,其实Node应该有一个参数是Parent。但是由于我有递归的方法并不需要所以就没写。
}
return root;
}
V delete() {
return null;
}
}
//递归的方式
static final class Notraverse<K extends Comparable <K>, V> extends RBTreeBase <K, V> {
Notraverse() {
super();
}
@Override
Node <K, V> findNode(K key) {
return findNode(getRoot(), key);
}
// 向以node为根的红黑树中插入元素(key, value),递归算法
// 返回插入新节点后红黑树的根
@Override
Node <K, V> addNode(Node <K, V> node, K key, V value) {
if (node == null) {
setSize();
return new Node(key, value); // 默认插入红色节点
}
if (key.compareTo(node.key) < 0)
node.left = addNode(node.left, key, value);
else if (key.compareTo(node.key) > 0)
node.right = addNode(node.right, key, value);
else // key.compareTo(node.key) == 0
node.value = value;
if (isRed(node.right) && !isRed(node.left))
node = leftRotate(node);
if (isRed(node.left) && isRed(node.left.left))
node = rightRotate(node);
if (isRed(node.left) && isRed(node.right))
flipColors(node);
return node;
}
// 递归的get写法
private Node <K, V> findNode(Node <K, V> node, K key) {
if (node == null)
return null;
int cmp = key.compareTo(node.key);
if (cmp == 0)
return node;
else if (cmp < 0)
return findNode(node.left, key);
else // if(cmp > 0)
return findNode(node.right, key);
}
V delete() {
return null;
}
}
public LRBTree(boolean traverse) {
rbTree = traverse == true ? new Traverse() : new Notraverse();
}
public boolean contains(K key) {
return get(key) != null;
}
public V get(K key) {
return rbTree.get(key);
}
public void put(K key, V value) {
rbTree.put(key, value);
}
public static void main(String[] args) {
LRBTree <Integer, Integer> map = new LRBTree <>(false);
map.put(36, 36);
map.put(34, 34);
map.put(37, 37);
map.put(33, 33);
map.put(35, 35);
map.put(32, 32);
map.put(29, 31);
System.out.println(map.get(6));
}
}
