WMD算法及python代码实现
本文目录
- 一、全篇概述
- 二、概念
- 1. Word2vec
- 2. nBOW representation
- 2. Word travel cost
- 3. Document distance
- 二、WMD
- 三、算法优化
- 1. WCD(word Centoid Distance)算法
- 2. RWMD(relaxed word moving distance)算法
- 3. Prefetch and prune
- 四、WMD优缺点
- 优点
- 缺点
- 五、python代码实现
本次讲解的论文来自J.Kusner等人2015年发表的论文,论文名字为From Word Embeddngs To Document Distances。
一、全篇概述
全篇最大的贡献是提出了WMD算法,并且为了提高计算速度,减低时间复杂度对模型进行了化简,得到WCD及RWMD算法,然后综合WCD及RWMD提出预取和修剪(Prefetch and prune),在几乎不影响算法准确率的情况下,大大提升了算法的计算效率。下面先介绍几个基本概念(预备知识),再一一讲解上面所提到的各种算法。
二、概念
1. Word2vec
Word2Vec是2013年由Mikolov等人提出的一种word emmbedding方法,简单的说就是将单词通过一个神经网络变为一个向量,用这个向量来表示这个单词,通过Word2Vec后得到的单词的向量表示在一定程度上保留了单词的语义信息,详见论文《Efficient Estimation of Word Representations in Vector Space》。
2. nBOW representation
nBOW全称normalized bag-of-words,即归一化词袋模型,就是对词袋中的词的一种向量表示,也可以从文档的角度理解,每一个文档都被表示成了一个向量。通过下面的例子可以很快理解nBOW representation。
假定数据集中只有两个文档:

经过删除停用词操作后,词袋中一共包含八个词,即上图中加粗的单词。
d i = c i ∑ j = 1 n c j d_i=\frac{c_i}{\sum_{j=1}^{n}{c_j}} di=∑j=1ncjci
我们用上式计算单词i在一个文档中的权重,其中ci表示单词i在某一文档中出现的次数,分母表示该文档的总的单词个数(除去停用词后的)。计算结果如下:

计算最后会得到一个m*n的矩阵,m为文档数量,n为词袋中单词个数。
2. Word travel cost
![]()
正如上式所示,单词的‘旅行成本’,就是两个单词的词向量之间的欧氏距离。
3. Document distance
D o c u m e n t d i s t a n c e 表 示 一 个 文 档 中 的 单 词 全 部 迁 移 到 另 一 个 文 档 的 总 成 本 , 可 以 表 示 为 ∑ i , j = 1 n T i j c ( i , j ) 其 中 T 是 一 个 矩 阵 , T i j > 0 表 示 单 词 i 有 多 少 迁 移 到 了 单 词 j . ∑ j = 1 n T i j = d i , ∀ i ∈ { 1 , 2 , . . . , n } , d 中 的 第 i 个 词 的 输 出 流 总 和 等 于 d i . ∑ i = 1 n T i j = d j ′ , ∀ j ∈ { 1 , 2 , . . . , n } , d 中 的 第 j 个 词 的 输 入 流 总 和 等 于 d j . Document \ distance表示一个文档中的单词全部迁移到另一个文档的总成本,可以表示为 \\ \sum_{i,j=1}^{n}{T_{ij}c(i,j)} \\ 其中T是一个矩阵,T_{ij}>0表示单词i有多少迁移到了单词j . \\ \sum_{j=1}^{n}{T_{ij}} = d_i,\forall i \in \{1,2,...,n\},d中的第i个词的输出流总和等于d_i. \\ \sum_{i=1}^{n}{T_{ij}} = d'_j,\forall j \in \{1,2,...,n\},d中的第j个词的输入流总和等于d_j. Document distance表示一个文档中的单词全部迁移到另一个文档的总成本,可以表示为i,j=1∑nTijc(i,j)其中T是一个矩阵,Tij>0表示单词i有多少迁移到了单词j.j=1∑nTij=di,∀i∈{1,2,...,n},d中的第i个词的输出流总和等于di.i=1∑nTij=dj′,∀j∈{1,2,...,n},d中的第j个词的输入流总和等于dj.
二、WMD
了 解 了 上 述 概 念 后 , W M D 算 法 就 非 常 好 理 解 , 它 就 是 把 两 个 文 档 的 距 离 表 示 为 D o c u m e n t d i s t a n c e 的 最 小 值 , 即 min T ≥ 0 ∑ i , j = 1 n T i j c ( i , j ) s u b j e c t t o : ∑ j = 1 n T i j = d i , ∀ i ∈ { 1 , 2 , . . . , n } , ∑ i = 1 n T i j = d j ′ , ∀ j ∈ { 1 , 2 , . . . , n } . 这 样 就 将 距 离 计 算 转 化 成 了 一 个 优 化 问 题 , 整 个 优 化 过 程 就 是 最 小 化 上 述 公 式 , 找 到 最 合 适 的 T 转 化 矩 阵 。 这 个 优 化 过 程 可 以 通 过 线 性 规 划 的 求 解 器 求 解 , 具 体 求 解 过 程 可 参 考 E M D 算 法 。 最 终 算 法 复 杂 度 为 O ( p 3 log p ) 。 了解了上述概念后,WMD算法就非常好理解,它就是把两个文档的距离表示为 \\ Document\ distance的最小值,即\min_{T\ge0}{\sum_{i,j=1}^{n}{T_{ij}c(i,j)}} \\ subject\ to:\sum_{j=1}^{n}{T_{ij}} = d_i,\forall i \in \{1,2,...,n\}, \\ \quad \qquad \qquad \sum_{i=1}^{n}{T_{ij}} = d'_j,\forall j \in \{1,2,...,n\}. \\ 这样就将距离计算转化成了一个优化问题,整个优化过程就是最小化上述公式,找到最合适的T转化矩阵 。 \\ 这个优化过程可以通过线性规划的求解器求解,具体求解过程可参考EMD算法。 \\ 最终算法复杂度为O(p^3\log p)。 了解了上述概念后,WMD算法就非常好理解,它就是把两个文档的距离表示为Document distance的最小值,即T≥0mini,j=1∑nTijc(i,j)subject to:j=1∑nTij=di,∀i∈{1,2,...,n},i=1∑nTij=dj′,∀j∈{1,2,...,n}.这样就将距离计算转化成了一个优化问题,整个优化过程就是最小化上述公式,找到最合适的T转化矩阵。这个优化过程可以通过线性规划的求解器求解,具体求解过程可参考EMD算法。最终算法复杂度为O(p3logp)。
示例:

三、算法优化
1. WCD(word Centoid Distance)算法
通过一个三角不等式将计算公式进行简化:
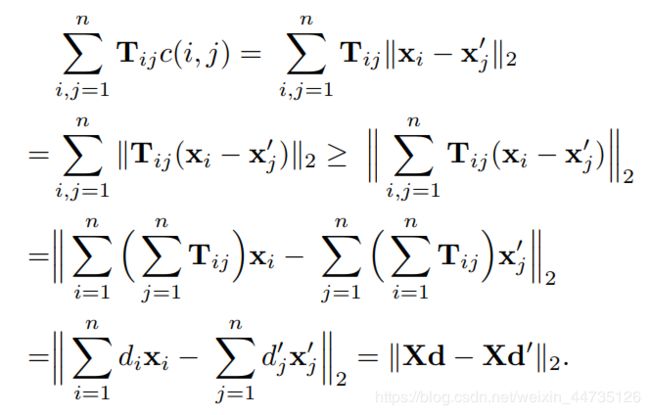
其 中 X 是 一 个 m ∗ n 的 矩 阵 , m 表 示 词 向 量 的 维 度 , n 表 示 词 库 中 所 有 词 的 个 数 , d 表 示 一 个 文 档 的 n B O W 向 量 。 其中X是一个m*n的矩阵,m表示词向量的维度,n表示词库中所有词的个数,d表示一个文档的nBOW向量。 其中X是一个m∗n的矩阵,m表示词向量的维度,n表示词库中所有词的个数,d表示一个文档的nBOW向量。
通过变换,计算变成了简单的矩阵计算,计算效率大大增高,时间复杂度为 O ( m n ) O(mn) O(mn).
但是计算的结果不准确,边界过于宽松,但对于那些需要求出相似度最大的n个句子的应用,可以通过 t o p − k top-k top−k的形式,对所有WCD值进行排序选择前K个进一步计算他们的准确的WMD值。
2. RWMD(relaxed word moving distance)算法
RWMD需要计算两次,基于WMD目标函数,分别去掉两个约束条件中的一个,然后求解最小值,使用两个最小值中的最大值作为WMD的近似值。
例如去掉第二个约束条件,这个问题的最优解变为:对于文本D1中的一个词,找到另一个文本D2中与之最相近的一个词,全部转移到这个词。即:
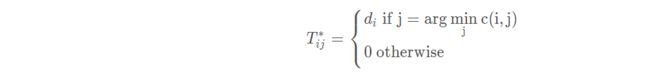
去掉第一个约束条件的计算方法与上述去掉第二个约束条件的方法类似,只有搜索最近单词时相反。两个计算可以同时计算可以大大节省计算成本。

RWMD的计算结果比WCD更接近WMD的精确结果。
3. Prefetch and prune
Prefetch and prune是上述两个优化算法的结合,主要针对查找一个句子的最相似的K个句子的问题。
首先对所有文档进行WCD计算,然后按照升序排序,然后选择前K个文档,计算它们的WMD值,对于剩余的文档计算他们的RWMD值,大于前K个中最大的WMD值的文档都删掉,没删掉的文档则进一步计算它们的WMD值,并加入top-k序列。
四、WMD优缺点
优点
- 无监督,不需要依赖数据标注。
- 不需要设置超参数。
- 创新点:将运输问题的解决方法EMD引入到文本相似度计算。
缺点
- 对于不在词袋中的词,只能删除,不能处理OOV(out of vocabulary)问题。
(对于专业术语较多的文档,效果不好。) - 词袋模型的通病,没有语序信息。
五、python代码实现
# Author Hans
import jieba
from gensim.models import Word2Vec
from gensim.similarities import WmdSimilarity
# 加载停用词
def get_stop_words(stop_words_dir):
stop_words = []
with open(stop_words_dir, 'r', encoding='utf-8') as f_reader:
for line in f_reader:
line = delete_r_n(line)
stop_words.append(line)
stop_words = set(stop_words)
return stop_words
# 去掉空字符
def delete_r_n(line):
return line.replace('\r', '').replace('\n', '').strip()
# 数据预处理
f = open(r'F:\python\data_structure_similarity\data\train_after_process_final.txt', 'r', encoding='utf-8') # 已经分好词并且已经去掉停用词的训练集文件
lines = f.readlines()
corpus = []
documents = []
# 加载停用词,stopwords为停用词列表
stopwords = get_stop_words(r'F:\python\data_structure_similarity\data\stop_words.txt')
# 建立语料库list文件(list中是已经分词后的)
for each in lines:
text = list(each.replace('\n', '').split(' '))
print(text)
corpus.append(text)
print(len(corpus))
# 建立相对应的原始语料库语句list文件(未分词)
with open(r'F:\python\data_structure_similarity\data\train.txt', 'r', encoding='utf-8') as f_1: # 未分词的原始train文件
f_1.readline()
for test_line in f_1:
test_line = delete_r_n(test_line) # 去掉空字符
print(test_line)
documents.append(test_line)
# 加载模型
print(20 * '*', '加载模型', 40 * '*')
pretrain_model_path = r'F:\python\data_structure_similarity\model\results\Pre_Train3000Epoch\SkipGram_Pre_Train3000Epoch.model'
model = Word2Vec.load(pretrain_model_path)
print("加载完成")
# 计算WMD(词移距离)的短文本相似度
# 初始化WmdSimilarity
num_best = 20
instance = WmdSimilarity(corpus, model, num_best=num_best)
print(20 * '*', '测试', 40 * '*')
sent = 'B+树是一种树数据结构,叶子结点存储关键字以及相应记录的地址,叶子结点以上各层作为索引使用。'
sent_w = list(jieba.cut(sent))
query = [w for w in sent_w if not w in stopwords]
# 在相似性类中的“查找”query
sims = instance[query]
# 返回相似结果
print('source_Query:')
print(sent)
for i in range(num_best):
print('sim = %.4f' % sims[i][1])
print('sims[i][0]:', sims[i][0])
print(documents[sims[i][0]])