Jakes信道模型总结

1.瑞利信道原理 http://blog.csdn.net/caozhk/article/details/19929435

      瑞利信道模型是无线通信信道最重要、最基础的的仿真模型。无线信道中的平坦衰落信道基本上都是在瑞利信道模型的基础上修改而成，比如应用同样广泛的莱斯信道就可以通过在瑞利信道的基础上简单的添加直流分量实现，而频率选择性衰落信道基本上都是几种平坦衰落信道叠加的结果。(怎么理解？)

   小尺度平坦衰落信道中，由于移动体处于不断的运动状态，导致接收端接收到的是来自不同路径的多径信号。移动台的速率将会导致每条多径分量具有不同的多普勒频移，同时假设移动台接收的信号的入射角度在[ 0, 2π]间均匀分布。这样就产生了具有特定环境下的多普勒功率谱密度特性。Clarke信道模型描述的小尺度平坦衰落信道中，移动台接收信号具有基于散射方式的场强统计特性，这正符合市区移动通信环境不存在直射路径的特点,其包络统计特性服从瑞利分布，因此又称为瑞利衰落信道模型。一般情况下，在 瑞利衰落的状态下，多普勒功率谱具有Jakes 功率谱密度函数,即U型谱。

  许多信道建模和仿真方法的研究，均以Clarke信道模型的统计特性作为性能评估的标准，但Clarke参考模型是一种理想模型，物理不可实现。Clarke参考模型是由多个正弦波相加，但要求个数非常大，理想统计特性在N为无穷大时取得。从对模型的仿真结果来看，一般需要在大于50个正弦波的条件下，才能取得较好的仿真效果。

2.瑞利信道仿真的实现方法

     Clarke参考模型的主要实现方法有正弦波叠加法和成型滤波法。两种方法各有其优缺点，正弦波叠加法由于计算复杂度低，在工业界得到广泛应用。

   正弦波叠加法

     正弦波叠加法是利用确定性过程来模拟随机过程。根据概率论，多个不同频率的正弦波叠加，幅度统计是服从高斯分布的。如果实部和虚部均用多个不同频率的正弦波叠加，则实部虚部均分别服从高斯分布。又根据瑞利分布的定义，两个高斯变量的平方和的根服从瑞利分布，因此包络服从瑞利分布。

   在仿真性能评估的角度来说，完全理想的情况下，各径的同相和正交分量应该完全不相关，两者合成的总自相关曲线有固定的变化趋势。这些也是评估正弦波叠加法实现算法性能的主要指标。

   正弦波叠加法易于实现，占用资源少，但是产生的多普勒功率谱是由多个离散频率点上的冲激构成的，并且相关性能不够理想。正弦波叠加法有很多种产生各正弦波相位、幅度参数的方法，比如等面积法，等距离法，蒙特卡罗法等，在这里不详细展开。

  Jakes提出了基于正弦波叠加法的Jakes仿真模型。Jakes仿真模型是一种确定模型，产生的信号非广义平稳且不具各态历经性，其二阶统计特性与Clarke参考模型也相差较大。Jakes仿真模型虽然对Clarke参考模型实现了简化，降低了复杂度，提高了仿真效率，但却引入了广义非平稳性。其主要原因就在于Jakes对模型中的随机相移进行了确定化，同时造成了随机相移之间存在相关性。在仿真效率方面，所需的低频振荡器（即正弦波发生器）的数目由N减小到M=(N/2一l)/2，运算量大大减少。

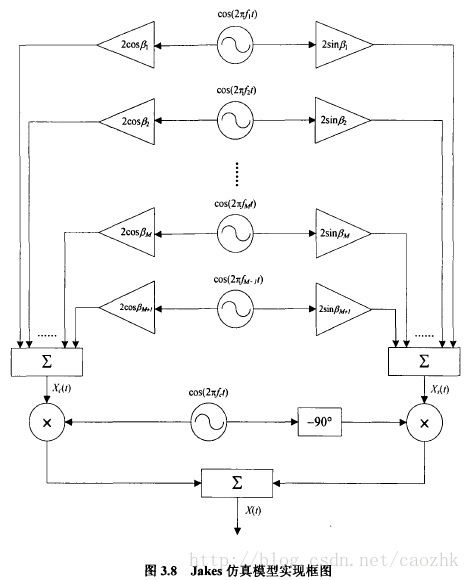
   基于Jakes仿真模型的多种改进方法,均是引入随机多普勒频率、随机正弦波初始相位等随机变量,避免确定性。

   某改进模型的方法是在低频振荡器中引入随机相移，避免了随机相移的确定化和相关性，从而使得广义平稳问题得到解决。此模型仅满足Clarke参考模型的一阶统计特性，二阶统计特性则不满足。另一改进模型的输出信号满足Clarke参考模型的二阶统计特性，但最大多普勒频移对应的正弦波对应两个随机相移，而其余多普勒频移位置对应的正弦波均对应四个随机相移，也就是对于每个多普勒频移都将所有随机相移考虑在内，因此并未引入随机相移的相关(不理解)。但由于每个多普勒频移项均要考虑所有随机相移，因此结构过于复杂。

  Y.R.Zheng和e.Xiao提出了多种改进的Jakes仿真模型，低频振荡器数目仅为M=8，一二阶统计特性同样符合Clarke参考模型理论值。文献[Yahong Rosa Zheng，Chengshan Xiao. ImProved Models for Generation of MultiPle Uneorrelated Rayleigh Fading Waveform 2002]给出了相应的结构图，每个正弦波需要三个随机量。

  下面给出Jakes方法的matlab实现代码，参见《MIMO-OFDM Wireless Communications with MATLAB》

function [h,tf]=Jakes_Flat(fd,Ts,Ns,t0,E0,phi_N)
% Inputs:
%   fd      : Doppler frequency
%   Ts      : sampling period
%   Ns      : number of samples
%   t0      : initial time
%   E0      : channel power
%   phi_N  : inital phase of the maximum doppler frequency sinusoid
% Outputs:
%   h       : complex fading vector
%   t_state: current time

%MIMO-OFDM Wireless Communications with MATLAB㈢   Yong Soo Cho, Jaekwon Kim, Won Young Yang and Chung G. Kang
%2010 John Wiley & Sons (Asia) Pte Ltd

if nargin<6,  phi_N=0;    end
if nargin<5,  E0=1;       end
if nargin<4,  t0=0;  end
if nargin<3,  error('More arguments are needed for Jakes_Flat()');   end
N0=8;                  % As suggested by Jakes 
N=4*N0+2;             % an accurate approximation              
wd=2*pi*fd;           % Maximum doppler frequency[rad]
%t_state = t0;
%for i=1:Ns
%   ich=sqrt(2)*cos(phi_N)*cos(wd*t_state);
%   qch=sqrt(2)*sin(phi_N)*cos(wd*t_state);
%   for k=1:N0
%      phi_n=pi*k/(N0+1);
%      wn=wd*cos(2*pi*k/N);
%      ich=ich+2*cos(phi_n)*cos(wn*t_state);
%      qch=qch+2*sin(phi_n)*cos(wn*t_state);
%   end
%   h1(i) = E0/sqrt(2*N0+1)*complex(ich,qch);
%   t_state=t_state+Ts;             % save last time
%end
t = t0+[0:Ns-1]*Ts;  tf = t(end)+Ts; 
coswt = [sqrt(2)*cos(wd*t); 2*cos(wd*cos(2*pi/N*[1:N0]')*t)]; % 侥 (2.32)
h = E0/sqrt(2*N0+1)*exp(j*[phi_N pi/(N0+1)*[1:N0]])*coswt; 
                                %侥 (2.29) with (2.30),(2.31), and (2.32)
% discrepancy = norm(h-h1)
% plot_Jakes_Flat.m

%MIMO-OFDM Wireless Communications with MATLAB㈢   Yong Soo Cho, Jaekwon Kim, Won Young Yang and Chung G. Kang
%2010 John Wiley & Sons (Asia) Pte Ltd

close all, clear all
% initial parameter
fd= 926;
Ts= 1e-6;
M= 2^12;
t= [0:M-1]*Ts;
f= [-M/2:M/2-1]/(M*Ts*fd);
Ns= 50000;
t_state= 0;
% channel generation
[h,t_state]=Jakes_Flat(fd,Ts,Ns,t_state,1,0);
% plotting
subplot(311), plot([1:Ns]*Ts,10*log10(abs(h))), axis([0 Ns*Ts -20 10])
title(['Channel Modeled by Jakes, f_d=',num2str(fd),'Hz, T_s=',num2str(Ts),'s']);
xlabel('time[s]'), ylabel('Magnitude[dB]')
subplot(323), hist(abs(h),50);
title(['Channel Modeled by Jakes, f_d=',num2str(fd),'Hz, T_s=',num2str(Ts),'s']);
xlabel('Magnitude'), ylabel('Occasions')
subplot(324), hist(angle(h),50);
title(['Channel Modeled by Jakes, f_d=',num2str(fd),'Hz, T_s=',num2str(Ts),'s']);
xlabel('Phase[rad]'), ylabel('Occasions')
% Autocorrelation of channel
temp=zeros(2,Ns);
for i=1:Ns
   j=i:Ns; temp1(1:2,j-i+1)= temp(1:2,j-i+1)+[h(i)'*h(j); ones(1,Ns-i+1)];
end
k=1:M; Simulated_corr(k)= real(temp(1,k))./temp(2,k);
Classical_corr= besselj(0,2*pi*fd*t);
% Fourier transform of autocorrelation
Classical_Y= fftshift(fft(Classical_corr));
Simulated_Y= fftshift(fft(Simulated_corr));
% plotting
subplot(325)
plot(t,abs(Classical_corr),'b:', t,abs(Simulated_corr),'r:')
title(['Autocorrelation of Channel, f_d=',num2str(fd),'Hz'])
grid on, xlabel('delay \tau [s]'), ylabel('Correlation')
legend('Classical','Simulated')
subplot(326)
plot(f,abs(Classical_Y),'b:', f,abs(Simulated_Y),'r:')
title(['Doppler Spectrum,f_d=',num2str(fd),'Hz'])
axis([-1 1 0 600]), xlabel('f/f_d'), ylabel('Magnitude')
legend('Classical','Simulated')

      

成型滤波法

    成形滤波器法是将高斯白噪声输入成形滤波器来产生指定形状的多普勒功率谱，实部和虚部均是具有特定形状多普勒功率谱的高斯有色噪声，因此包络服从瑞利分布。

基于频域仿真的瑞利衰落仿真结构图

   由于通常情况下通信系统的采样好速率非常高，最大多普勒频率与采样率相比很小，因此成形滤波器需要的带宽很小，直接实现非常困难。一般是高斯噪声通过低采样率的滤波器滤波后不断进行内插来实现，得到与系统数据速率相等的抽头系数(不理解)。需要进行多级内插和IFFT，消耗的计算存储资源很多，不适宜用于大数据量的信道仿真。但是成形滤波器法是用随机噪声产生的，因而随机性比正弦波叠加法，各方面性能更为理想。

   其中滤波过程可以采用频域滤波或时域滤波。时域滤波可以通过改变高斯信号源长度任意扩展信道长度，但计算量非常大大，而频域滤波受到IFFT长度的限制，计算量较大。对于时域滤波，使用重叠相加法可以改善复杂度。

  对于滤波，一般以大约为系统最高Doppler频移的8到12倍速率对信号进行采样，能得到满意的结果。系统数据传送速率与这个采样频率的比值为抽样(内插)因子。对滤波器的输出以内插因子作内插，可以得到和系统数据速率匹配的信道抽头系数，即信道响应。

  给出频域滤波的matlab实现代码如下，参见《MIMO-OFDM Wireless Communications with MATLAB》：

function [h,tf]=Jakes_Flat(fd,Ts,Ns,t0,E0,phi_N)
% Inputs:
%   fd      : Doppler frequency
%   Ts      : sampling period
%   Ns      : number of samples
%   t0      : initial time
%   E0      : channel power
%   phi_N  : inital phase of the maximum doppler frequency sinusoid
% Outputs:
%   h       : complex fading vector
%   t_state: current time

%MIMO-OFDM Wireless Communications with MATLAB㈢   Yong Soo Cho, Jaekwon Kim, Won Young Yang and Chung G. Kang
%?2010 John Wiley & Sons (Asia) Pte Ltd

if nargin<6,  phi_N=0;    end
if nargin<5,  E0=1;       end
if nargin<4,  t0=0;  end
if nargin<3,  error('More arguments are needed for Jakes_Flat()');   end
N0=8;                  % As suggested by Jakes 
N=4*N0+2;             % an accurate approximation              
wd=2*pi*fd;           % Maximum doppler frequency[rad]
%t_state = t0;
%for i=1:Ns
%   ich=sqrt(2)*cos(phi_N)*cos(wd*t_state);
%   qch=sqrt(2)*sin(phi_N)*cos(wd*t_state);
%   for k=1:N0
%      phi_n=pi*k/(N0+1);
%      wn=wd*cos(2*pi*k/N);
%      ich=ich+2*cos(phi_n)*cos(wn*t_state);
%      qch=qch+2*sin(phi_n)*cos(wn*t_state);
%   end
%   h1(i) = E0/sqrt(2*N0+1)*complex(ich,qch);
%   t_state=t_state+Ts;             % save last time
%end
t = t0+[0:Ns-1]*Ts;  tf = t(end)+Ts; 
coswt = [sqrt(2)*cos(wd*t); 2*cos(wd*cos(2*pi/N*[1:N0]')*t)]; % 侥 (2.32)
h = E0/sqrt(2*N0+1)*exp(j*[phi_N pi/(N0+1)*[1:N0]])*coswt; 
                                % (2.29) with (2.30),(2.31), and (2.32)
% discrepancy = norm(h-h1)
function [FadTime,tf] = FWGN_ff(Np,fm_Hz,Nfading,Nfosf,FadingType,varargin)
%Fadng generation based on FWGN method
% FadTime= FWGN_ff(Np,fm_Hz,Nfading,Nfosf,FadingType,sigma,phi)
% Inputs:
%  Np         : # of multipath
%  fm_Hz      : A vector of max. Doppler frequency of each path[Hz]
%  Nfading    : Doppler filter size (IFFT size)
%  Nfosf      : Oversampling factor of Doppler bandwith
%  FadingType : Doppler type, 'laplacian'/'class'/'flat'
%  sigma      : Angle spread of UE in case of 'laplacian' Doppler type
%  phi        : DoM-AoA in case of 'laplacian' Doppler type
% Outputs:
%  FadTime    : Np x Nfading, fading time matrix

%MIMO-OFDM Wireless Communications with MATLAB㈢   Yong Soo Cho, Jaekwon Kim, Won Young Yang and Chung G. Kang
%?2010 John Wiley & Sons (Asia) Pte Ltd

fmax= max(fm_Hz);
% Doppler frequency spacing respect to maximal Doppler frequency
dfmax= 2*Nfosf*fmax/Nfading; 
if isscalar(fm_Hz), fm_Hz= fm_Hz*ones(1,Np);  end
% To get a funtion corresponding to Doppler spectrum of "FadingType"
FadingType= lower(FadingType); ftn_psd= Doppler_PSD_function(FadingType);
err_msg= 'The difference between max and min Doppler frequencies is too large.\n increase the IFFT size'; 
if strcmp(FadingType(1:2),'la') % Laplacian constrained PAS
  for i=1:Np
     Nd= floor(fm_Hz(i)/dfmax)-1;
     if Nd<1,  error(err_msg);   end
     tmp= ftn_psd([-Nd:Nd],varargin{1}(i),varargin{2}(i));
     tmpz= zeros(1,Nfading-2*Nd+1);
     FadFreq(i,:)= [tmp(Nd+1:end-1) tmpz tmp(2:Nd)];
  end
 else  % symmetric Doppler spectrum
  for i=1:Np
     Nd= floor(fm_Hz(i)/dfmax)-1;
     if Nd<1,  error(err_msg);  end
     tmp= ftn_psd([0:Nd]/Nd); tmpz= zeros(1,Nfading-2*Nd+3);
     FadFreq(i,:)= [tmp(1:Nd-1) tmpz fliplr(tmp(2:Nd-1))];
  end
end
% Add a random phase to the Doppler spectrum
FadFreq = sqrt(FadFreq).*exp(2*pi*j*rand(Np,Nfading));
FadTime = ifft(FadFreq,Nfading,2);
% Normalization to 1
FadTime= FadTime./sqrt(mean(abs(FadTime).^2,2)*ones(1,size(FadTime,2)));
tf=1/(2*fmax*Nfosf); %fading sample time=1/(Doppler BW*Nfosf)