LeetCode - 152. Maximum Product Subarray(子数组最大累乘积)
LeetCode - 152. Maximum Product Subarray(子数组最大累乘积)
- 一维dp
- 滚动优化
- 递归版本
题目链接
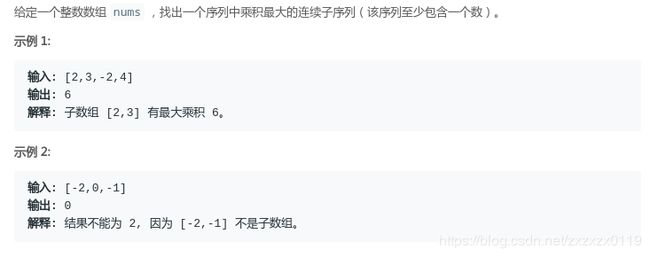
题目
这题和LeetCode53类似。
一维dp
使用一个一维数组记录以每个位置结尾的最大累乘积,再使用一个res变量(记录结果),记录每一个位置结尾ends[i]的最大值。
如何快速求出所有以i位置结尾(nums[i])的子数组的最大累乘积? 假设以nums[i-1]结尾的最大累乘积为maxEnds[i-1],以nums[i-1]记为的最小累乘积为minEnds[i-1],那么以nums[i]结尾的最大累乘积只有三种可能
- 可能是
maxEnds[i-1] * nums[i],这个是显然的,因为记录前面的最大值,如[3,4,5]; - 可能是
minEnds[i-1] * nums[i],因为minEnds[i-1]和nums[i]都有可能是负数,如[-2,-4]; - 也有可能是
nums[i]自己;
则以这个结尾的最大值maxEnds[i]就是这三者中的最大的一个。 而minEnds[i]的更新就是这三者中的最小的一个。
class Solution {
public int maxProduct(int[] nums) {
if (nums == null || nums.length == 0)
return 0;
int[] minEnds = new int[nums.length];
int[] maxEnds = new int[nums.length];
minEnds[0] = nums[0];
maxEnds[0] = nums[0];
int res = nums[0];
for (int i = 1; i < nums.length; i++) {
int max = nums[i] * maxEnds[i - 1];
int min = nums[i] * minEnds[i - 1];
maxEnds[i] = Math.max(max, Math.max(min, nums[i]));
minEnds[i] = Math.min(min, Math.min(max, nums[i]));
res = Math.max(maxEnds[i], res);
}
return res;
}
}
滚动优化
这里的滚动优化就是当前位置只依赖前一个位置的最大和最小值,所以只需要两个变量即可。
优化空间:
class Solution {
public int maxProduct(int[] nums) {
if (nums == null || nums.length == 0)
return 0;
int minEnd = nums[0];
int maxEnd = nums[0];
int res = nums[0];
for (int i = 1; i < nums.length; i++) {
int max = nums[i] * maxEnd;
int min = nums[i] * minEnd;
maxEnd = Math.max(max, Math.max(min, nums[i]));
minEnd = Math.min(min, Math.min(max, nums[i]));
res = Math.max(maxEnd, res);
}
return res;
}
}
递归版本
能用dp的基本都能写出递归,能写出递归的都可以改dp;
但是这里要注意:
- 当从最后一个计算完之后,因为在
return前记录的res,所以最后一个没有记录; - 所以在调用完函数之后,存储返回值,再比较一下
last和res的值,然后返回;
class Solution {
private int res;
public int maxProduct(int[] nums) {
if (nums == null || nums.length == 0)
return 0;
res = nums[0];
int last = maxMul(nums, nums.length - 1); // 最后一个不要忘了比较
res = Math.max(res, last);
return res;
}
private int maxMul(int[] arr, int i) {
if (i == 0)
return arr[0];
int preMax = maxMul(arr, i - 1);
int preMin = minMul(arr, i - 1);
res = Math.max(res, preMax);
return Math.max(preMax * arr[i],
Math.max(preMin * arr[i], arr[i])
);
}
private int minMul(int[] arr, int i) {
if (i == 0)
return arr[0];
int preMin = minMul(arr, i - 1);
int preMax = maxMul(arr, i - 1);
return Math.min(preMin * arr[i],
Math.min(preMax * arr[i], arr[i])
);
}
}
递归改记忆化,记忆化代码可以通过,不过在递归之后还要比较一次,注意细节:
class Solution {
private int res;
//记忆化
private int[] maxEnds;
private int[] minEnds;
public int maxProduct(int[] nums) {
if (nums == null || nums.length == 0)
return 0;
res = nums[0];
maxEnds = new int[nums.length];
Arrays.fill(maxEnds, Integer.MIN_VALUE);
minEnds = new int[nums.length];
Arrays.fill(minEnds, Integer.MAX_VALUE);
int last = maxMul(nums, nums.length - 1); // 最后一个不要忘了比较
res = Math.max(res, last);
return res;
}
private int maxMul(int[] arr, int i) {
if (i == 0)
return arr[0];
if (maxEnds[i] != Integer.MIN_VALUE)
return maxEnds[i];
int preMax = maxMul(arr, i - 1);
int preMin = minMul(arr, i - 1);
res = Math.max(res, preMax);
maxEnds[i] = Math.max(preMax * arr[i],
Math.max(preMin * arr[i], arr[i])
);
return maxEnds[i];
}
private int minMul(int[] arr, int i) {
if (i == 0)
return arr[0];
if (minEnds[i] != Integer.MAX_VALUE)
return minEnds[i];
int preMin = minMul(arr, i - 1);
int preMax = maxMul(arr, i - 1);
minEnds[i] = Math.min(preMin * arr[i],
Math.min(preMax * arr[i], arr[i])
);
return minEnds[i];
}
}
也可以稍微改动一下,就不需要单独处理最后一个last了,在记忆化返回之前记录res的最大值:
class Solution {
private int res;
//记忆化
private int[] maxEnds;
private int[] minEnds;
public int maxProduct(int[] nums) {
if (nums == null || nums.length == 0)
return 0;
res = nums[0];
maxEnds = new int[nums.length];
Arrays.fill(maxEnds, Integer.MIN_VALUE);
minEnds = new int[nums.length];
Arrays.fill(minEnds, Integer.MAX_VALUE);
maxMul(nums, nums.length - 1);
return res;
}
private int maxMul(int[] arr, int i) {
if (i == 0)
return arr[0];
if (maxEnds[i] != Integer.MIN_VALUE)
return maxEnds[i];
int preMax = maxMul(arr, i - 1);
int preMin = minMul(arr, i - 1);
maxEnds[i] = Math.max(preMax * arr[i],
Math.max(preMin * arr[i], arr[i])
);
res = Math.max(res, maxEnds[i]);
return maxEnds[i];
}
private int minMul(int[] arr, int i) {
if (i == 0)
return arr[0];
if (minEnds[i] != Integer.MAX_VALUE)
return minEnds[i];
int preMin = minMul(arr, i - 1);
int preMax = maxMul(arr, i - 1);
minEnds[i] = Math.min(preMin * arr[i],
Math.min(preMax * arr[i], arr[i])
);
return minEnds[i];
}
}