关于梯度算法
- 1. 前言
- 2. 数据准备
- 3. 批量梯度下降
- 4. 随机梯度下降
- 5. 小批量梯度下降
- 总结
1. 前言
- 关于梯度算法相关知识上篇文章已经做过简单的介绍,本篇文章对于梯度算法如何用Python代码实现做一下详细介绍。
2. 数据准备
import numpy as np
import os
import matplotlib.pyplot as plt
%matplotlib inline
- 为了便于保存我们所绘制的图片,创建一个保存图片的函数
np.random.seed(42)
PROJECT_ROOT_DIR = "."
MODEL_ID = "linear_model"
def save_fig(fig_id,tight_layout = True):
path = os.path.join(PROJECT_ROOT_DIR,"images",MODEL_ID,fig_id + ".png")
print("Saving figure",fig_id)
plt.savefig(path,format = 'png',dpi = 300)
import warnings
warnings.filterwarnings(action = "ignore",message = "^internal gelsd")
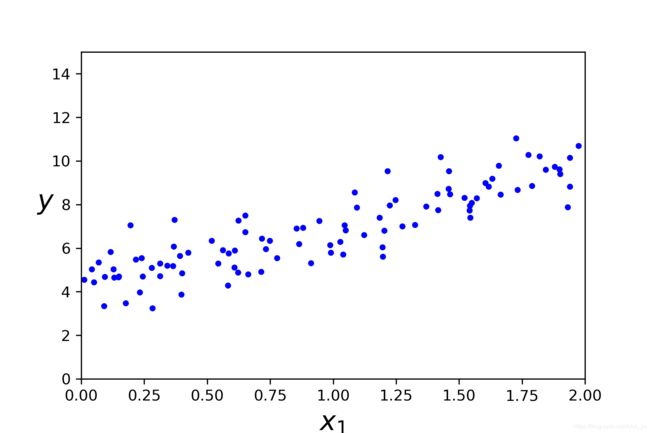
X = 2 * np.random.rand(100,1)
Y = 4 + 3 * X + np.random.randn(100,1)
plt.plot(X,Y,"b.")
plt.xlabel("$x_1$",fontsize = 18)
plt.ylabel("$y$",rotation = 0,fontsize = 18)
plt.axis([0,2,0,15])
save_fig("generated_data_plot")
plt.show()
X_b = np.c_[np.ones((100,1)),X]
X_new = np.array([[0],[2]])
X_new_b = np.c_[np.ones((2,1)),X_new]
3. 批量梯度下降
eta = 0.1
n_iterations = 1000
m = 100
theta = np.random.randn(2,1)
for iteration in range(n_iterations):
gradients = 2/m * X_b.T.dot(X_b.dot(theta) - Y)
theta = theta - eta * gradients
theta_path_bgd = []
def plot_gradient_descent(theta,eta,theta_path = None):
m = len(X_b)
plt.plot(X,Y,"b.")
n_iterations = 1000
for iteration in range(n_iterations):
if iteration < 10:
y_predict = X_new_b.dot(theta)
style = "b-"
plt.plot(X_new,y_predict,style)
gradients = 2/m * X_b.T.dot(X_b.dot(theta) - Y)
theta = theta - eta * gradients
if theta_path is not None:
theta_path.append(theta)
plt.xlabel("$x_1$",fontsize = 18)
plt.axis([0,2,0,15])
plt.title(r"$\eta = {}$".format(eta),fontsize = 16)
np.random.seed(42)
theta = np.random.randn(2,1)
plt.figure(figsize = (10,4))
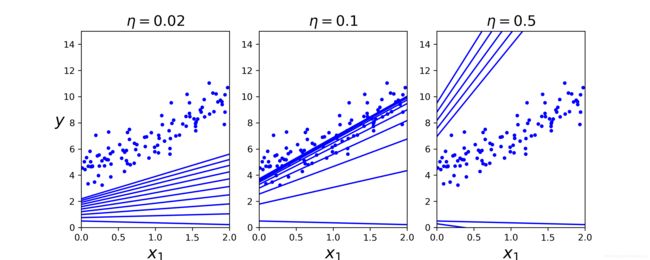
plt.subplot(131);plot_gradient_descent(theta,eta = 0.02)
plt.ylabel('$y$',rotation = 0,fontsize = 18)
plt.subplot(132);plot_gradient_descent(theta,eta = 0.1,theta_path = theta_path_bgd)
plt.subplot(133);plot_gradient_descent(theta,eta = 0.5)
save_fig("gradient_descent_plot")
- 效果图
4. 随机梯度下降
theta_path_sgd = []
m = len(X_b)
np.random.seed(42)
n_epochs = 5
theta = np.random.randn(2,1)
for epoch in range(n_epochs):
for i in range(m):
if epoch == 0 and i < 20:
y_predict = X_new_b.dot(theta)
style = "b-"
plt.plot(X_new,y_predict,style)
random_index = np.random.randint(m)
xi = X_b[random_index:random_index + 1]
yi = Y[random_index:random_index + 1]
gradients = 2 * xi.T.dot(xi.dot(theta) - yi)
eta = 0.1
theta = theta - eta * gradients
theta_path_sgd.append(theta)
plt.plot(X,Y,"b.")
plt.xlabel("$x_1$",fontsize = 18)
plt.ylabel("$y$",rotation = 0,fontsize = 18)
plt.axis([0,2,0,15])
save_fig("sgd_plot")
plt.show()
- 效果图
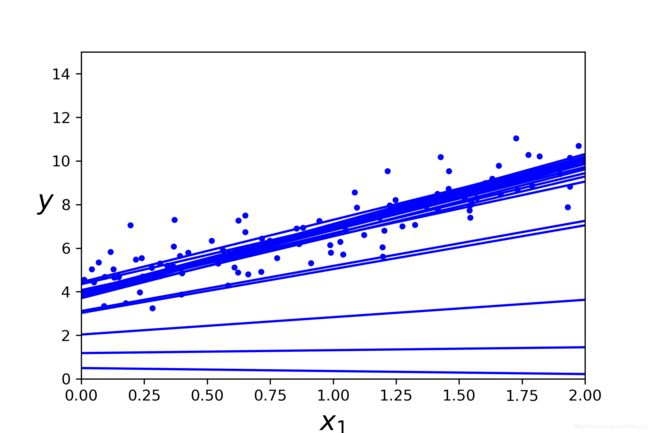
- 我们也可以直接导入包来求解
from sklearn.linear_model import SGDRegressor
sgd_reg = SGDRegressor(max_iter = 50,tol = -np.infty,penalty = None,eta0 = 0.1,random_state = 42)
sgd_reg.fit(X,Y.ravel())
sgd_reg.intercept_,sgd_reg.coef_
(array([4.16782089]), array([2.72603052]))
5. 小批量梯度下降
theta_path_mgd = []
n_iterations = 50
minibatch_size = 20
np.random.seed(42)
theta = np.random.randn(2,1)
for epoch in range(n_iterations):
shuffled_indices = np.random.permutation(m)
X_b_shuffled = X_b[shuffled_indices]
y_shuffled = Y[shuffled_indices]
for i in range(0,m,minibatch_size):
xi = X_b_shuffled[i:i + minibatch_size]
yi = y_shuffled[i:i + minibatch_size]
gradients = 2/minibatch_size * xi.T.dot(xi.dot(theta) - yi)
eta = 0.1
theta = theta - eta * gradients
theta_path_mgd.append(theta)
theta_path_bgd = np.array(theta_path_bgd)
theta_path_sgd = np.array(theta_path_sgd)
theta_path_mgd = np.array(theta_path_mgd)
plt.figure(figsize = (7,4))
plt.plot(theta_path_sgd[:,0],theta_path_sgd[:,1],"r-s",linewidth = 1,label = "Stochastic")
plt.plot(theta_path_mgd[:,0],theta_path_mgd[:,1],"g-+",linewidth = 2,label = "Minni-batch")
plt.plot(theta_path_bgd[:,0],theta_path_bgd[:,1],"b-o",linewidth = 3,label = "Batch")
plt.legend(loc = "upper left",fontsize = 16)
plt.xlabel(r"$\theta_0$",fontsize = 20)
plt.ylabel(r"$\theta_1$",fontsize = 20,rotation = 0)
plt.axis([2.5,4.5,2.3,3.9])
save_fig("gradient_descent_paths_plot")
plt.show()
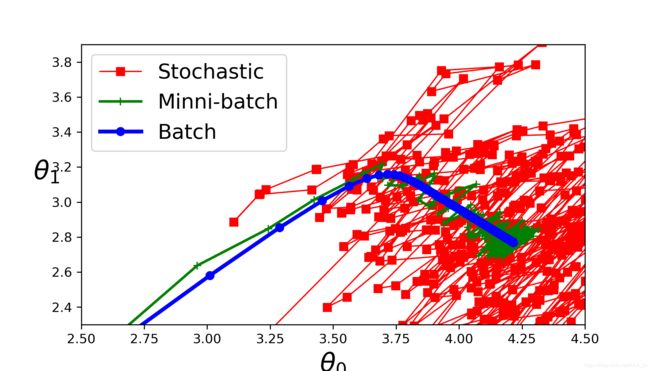
- 效果图
总结
- 从三种算法的比较图中可以直观地看出BGD的收敛速度最快,而SGD因为每次计算仅使用了一个样本点,所以收敛速度最慢,MBGD介于BGD和SGD之间,每次计算时使用了多个样本,因为每次使用的样本数不确定,也就是梯度的方向不定,所以相对于BGD则需要更多地时间来接近最小值点。



