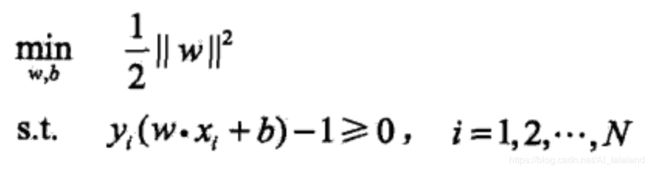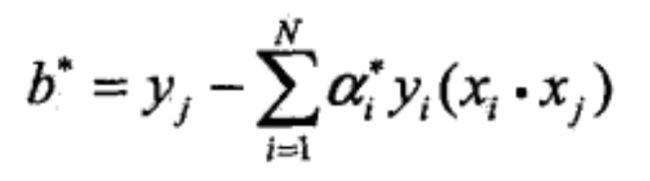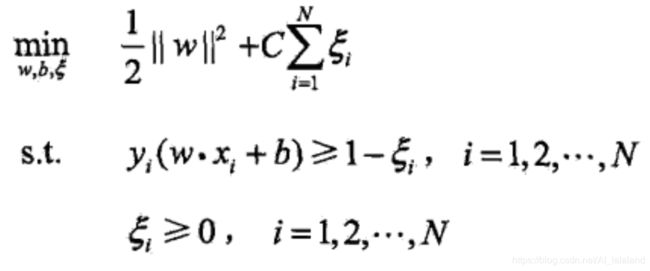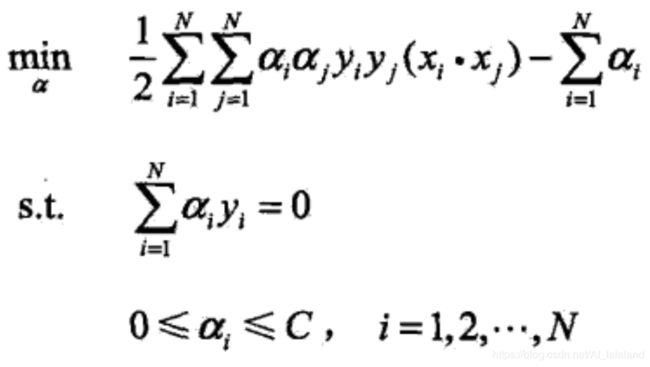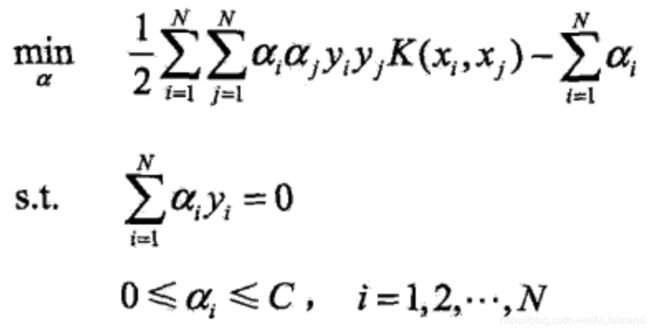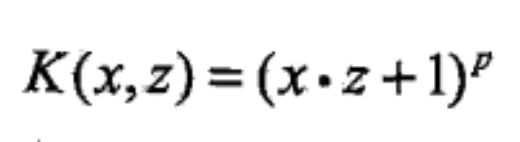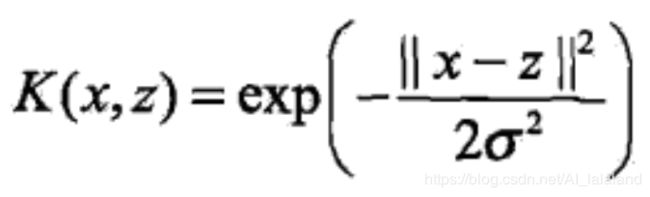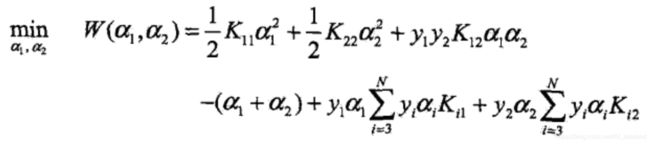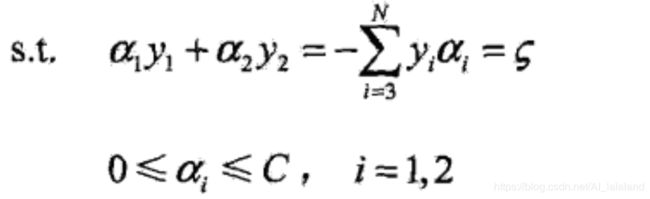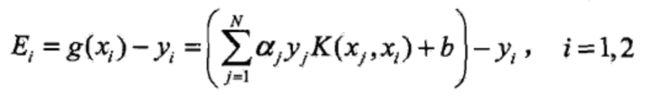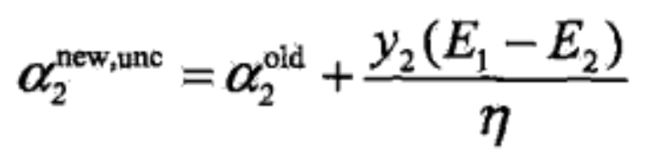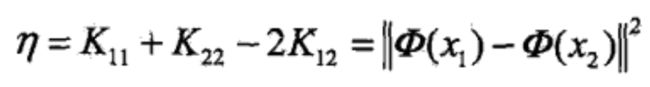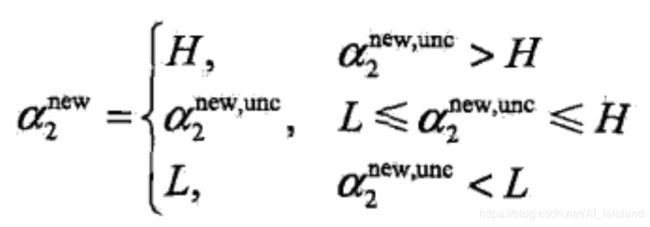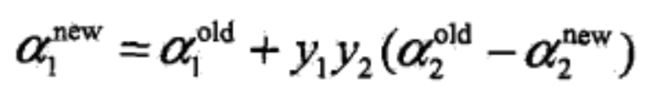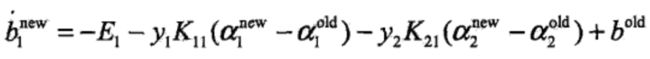机器学习实战_Python3.7_支持向量机SVM

SVM 算法原理

SVM 基本思想是依据“间隔最大化”，构建超平面将特征空间一分为二，用于分类。

SVM 可分为三类：

• 线性可分 SVM
• 线性 SVM
• 非线性 SVM

---

线性可分 SVM 用于处理线性可分的数据，其分类结果是“完美”的、唯一的。求解目标是使得“硬间隔最大化”的超平面，可抽象表达为：

解得 ω 、b 即可表示超平面 ω·x + b = 0。

这是一个凸优化问题，直接求解比较困难。解决方法是根据拉格朗日对偶性，引入拉格朗日乘子 α ，找到这个原始问题的对偶问题，对对偶问题求解等同于对原始问题求解：

解得 α 可转换为原问题的 ω 、b：

 

其中 yj 对于 α* 中的一个正分量 αj*。

说明：ω* 、b* 的求解只和 α* 中大于 0 的分量有关，即只和处在间隔边界上的样本有关，称为支持向量。

---

线性 SVM 用于处理线性不可分但近似可分的数据，在线性可分 SVM 的基础之上引入松弛变量 ξ ，惩罚参数 C ，根据惩罚参数 C 设定的不同，其分类结果是不同的。求解目标是使得“软间隔最大化”的超平面，可抽象表达为：

同样的，引入拉格朗日乘子，获得其对偶问题：

解得 α 转换为原问题的 ω 、b 的公式和线性可分 SVM 中相同。

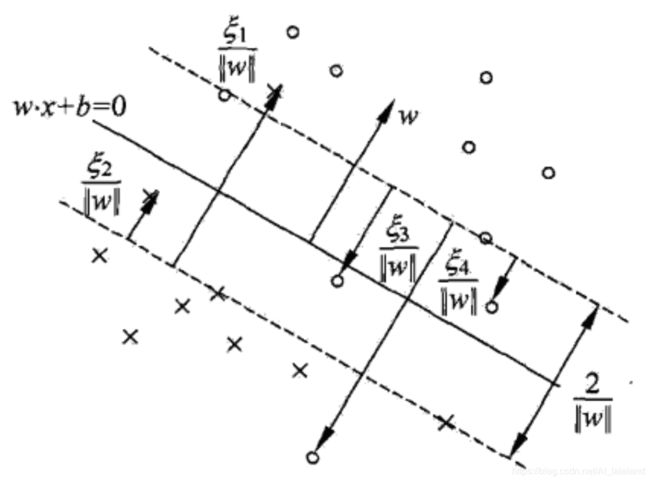
说明：软间隔的支持向量 xi 情况要相对复杂，可以在间隔边界上，可以在间隔边界到超平面之间，也可以在超平面误分一侧。

图示实线为超平面，有 ω·x + b = 0；下方虚线为负样本的间隔边界，可以用 ω·x + b = -1 表示；上方虚线为正样本的间隔边界，可以用 ω·x + b = 1 表示。

支持向量 xi 的位置可以根据 αi 和 ξi 的值进行判断：

• αi < C：xi 位于间隔边界上（ ξi = 0，分类正确）
• αi = C 且 0 < ξi < C：xi 位于间隔边界到超平面之间（分类正确）
• αi = C 且 ξi = C：xi 位于超平面上（正样本则分类正确，负样本则分类错误）
• αi = C 且 ξi > C：xi 位于超平面误分一侧（分类错误）

---

非线性 SVM 用于处理线性不可分的数据，引入核技巧，将特征集由欧式空间映射到希尔伯特空间，用线性分类的方法处理线性不可分的数据。

用核函数替代简单的 x 向量内积，将线性 SVM 的对偶问题转化为：

其中常用的核函数有多项式核函数和高斯核函数，表达式分别为：

 其余内容和线性 SVM 一致。

---

---

SVM 的实现 —— SMO 算法

对于数据集很大时，直接对 SVM 的对偶问题求解变得困难，通常需要使用能够快速实现的算法，求近似解，这里使用的是序列最小最优化算法，简称 SMO 算法。

SMO 算法是一种启发式算法，不同时对 α 向量的所有分量求解，而是每次对其中两个分量进行优化，将 SVM 的对偶问题分割成子问题：

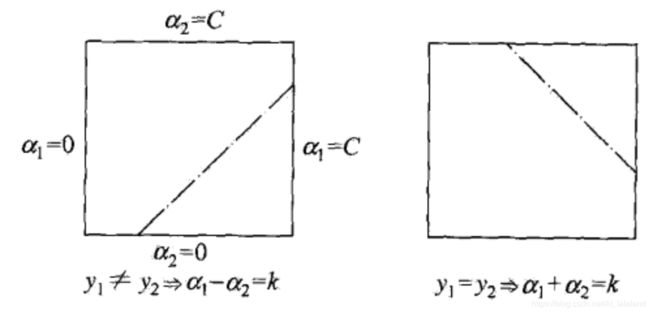
这里变成了两个变量的二次规划问题，两个限制条件可以图形化表示：

首先根据如下公式计算 Ei 和 Ej：

然后计算未剪辑的，沿着约束方向的 α2 的最优解：

其中：

接着计算剪辑后最终得到的 α2 的最优解：

以及 α1 的最优解：

---

外层循环用于选择第一个变量  α1，选择依据是违反 KKT 条件最严重的样本点。

内层循环用于选择第二个变量  α2，选择依据是希望 α2 有足够大的变化。

注意：为了快速计算，算法过程需要缓存 Ei 的值。

每次完成两个变量的优化之后，要更新 b：

若得到的新的 α1 满足 0 < α1 < C，可直接计算 b：

 若得到的新的 α2 满足 0 < α2 < C，可直接计算 b：

 若 α1、α2 都不满足，则按取 b1、b2 的均值作为 b。

更新 b 之后，还要根据公式更新 E1、E2：

---

---

 程序

from numpy import *

# 建立对象，保存：
# 1、特征集 dataMatIn 和 标签集 classLabels
# 2、参数 C：惩罚参数；参数 toler：允许误差；参数 kTup：设置核函数
# 3、alphas 和 b
# 4、辅助计算的 eCache：缓存 Ei
# 5、核函数的参数设置 hTup
class optStruct:
    def __init__(self,dataMatIn, classLabels, C, toler, kTup):
        self.X = dataMatIn
        self.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m = shape(dataMatIn)[0]
        self.alphas = mat(zeros((self.m,1)))
        self.b = 0
        # eCache[0] 为有效位
        # eCache[1] 为数值位
        self.eCache = mat(zeros((self.m,2)))
        # 矩阵 K[i][j] 代表核函数 K(xi,xj)
        self.K = mat(zeros((self.m,self.m)))
        for i in range(self.m):
            self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)

# 辅助函数：用于计算核
# 输入 X 为整个特征集
# 输入 A 为某个样本的特征
# 输入 kTup 为核函数参数
def kernelTrans(X, A, kTup):
    m,n = shape(X)
    K = mat(zeros((m,1)))
    # 线性核
    if kTup[0]=='lin':
        K = X * A.T
    # 高斯核
    elif kTup[0]=='rbf':
        for j in range(m):
            deltaRow = X[j,:] - A
            K[j] = deltaRow * deltaRow.T
        K = exp(K / (-1 * kTup[1] ** 2))
    # 错误
    else: raise NameError('Houston We Have a Problem -- That Kernel is not recognized')
    return K

#################################################################################################

# 辅助函数：将 aj 修订到 L ～ H 范围内
def clipAlpha(aj,H,L):
    if aj > H:
        aj = H
    if aj < L:
        aj = L
    return aj

# 辅助函数：用于计算 Ek
# 返回 K 中的 K[:][k]
def calcEk(oS, k):
    fXk = float(multiply(oS.alphas, oS.labelMat).T * oS.K[:, k] + oS.b)
    Ek = fXk - float(oS.labelMat[k])
    return Ek

# 辅助函数：缓存 Ek，并将有效位置 1
def updateEk(oS, k):
    Ek = calcEk(oS, k)
    oS.eCache[k] = [1, Ek]

# SMO 内循环
def innerL(i, oS):
    # 对 alpha i 计算 Ei
    Ei = calcEk(oS, i)
    # 如果满足条件：0 < alpha i < C ，且误差 Ei 大于预设定的 toler
    if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
        # 找到 alpha j 并计算 Ej
        j,Ej = selectJ(i, oS, Ei)
        # 记录更改前的 alpha i 和 alpha j
        alphaIold = oS.alphas[i].copy()
        alphaJold = oS.alphas[j].copy()
        # 计算 L 和 H
        if (oS.labelMat[i] != oS.labelMat[j]):
            L = max(0, oS.alphas[j] - oS.alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])
        if L==H:
            print("L == H")
            return 0
        # 更新 alpha i 和 alpha j 并更新 eCache
        eta = oS.K[i,i] + oS.K[j,j] - 2.0 * oS.K[i,j]
        if eta <= 0:
            print("eta <= 0")
            return 0
        oS.alphas[j] += oS.labelMat[j] * (Ei - Ej) / eta
        oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
        updateEk(oS, j)
        if (abs(oS.alphas[j] - alphaJold) < 0.00001):
            print("j not moving enough")
            return 0
        oS.alphas[i] += oS.labelMat[j] * oS.labelMat[i] * (alphaJold - oS.alphas[j])
        updateEk(oS, i)
        # 计算 b
        b1 = oS.b - Ei - oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
        b2 = oS.b - Ej - oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]
        if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]):
            oS.b = b1
        elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]):
            oS.b = b2
        else:
            oS.b = (b1 + b2)/2.0
        return 1
    else: return 0

#################################################################################################

# 辅助函数：随机选取 0～m 中一个不等于 i 的整数
def selectJrand(i,m):
    j = i
    while (j == i):
        j = int(random.uniform(0,m))
    return j

# 辅助函数：用于选择第二个 alpha（内循环）
# 选择方式：Ej 与 Ei 差值最大
def selectJ(i, oS, Ei):
    maxK = -1
    maxDeltaE = 0
    Ej = 0
    # eCache[i] 有效位置 1，并保存 Ei
    oS.eCache[i] = [1, Ei]
    # 得到所有有效位为 1 的 Ek 对应的下标 k 组成的列表
    validEcacheList = nonzero(oS.eCache[:, 0].A)[0]
    # 如果存在有效位为 1 的 Ek：找到与 Ei 差值最大的 Ek，作为 Ej 返回
    if (len(validEcacheList)) > 1:
        for k in validEcacheList:
            if k == i:
                continue
            Ek = calcEk(oS, k)
            deltaE = abs(Ei - Ek)
            if (deltaE > maxDeltaE):
                maxK = k
                maxDeltaE = deltaE
                Ej = Ek
        return maxK, Ej
    # 没有有效位为 1 的 Ek（第一次循环时）：随机选取一个 Ej 返回
    else:
        j = selectJrand(i, oS.m)
        Ej = calcEk(oS, j)
    return j, Ej

# SMO 外循环
def smoP(dataMatIn, classLabels, C, toler, maxIter, kTup=('lin', 0)):
    # 初始化 oS 对象
    oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(), C, toler, kTup)
    # 记录迭代次数
    iter = 0
    # 标记本次迭代方式
    entireSet = True
    # 记录本次迭代 alpha 改变次数
    alphaPairsChanged = 0
    # 当迭代次数超过到最大值，或者遍历整个集合都未对 alpha 修改，则退出循环
    while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
        alphaPairsChanged = 0
        # 遍历所有样本
        if entireSet:
            for i in range(oS.m):
                alphaPairsChanged += innerL(i,oS)
                print("fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
            iter += 1
        # 遍历所有非边界样本（alpha 不等于 0 或者 C）
        else:
            nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
            for i in nonBoundIs:
                alphaPairsChanged += innerL(i,oS)
                print("non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
            iter += 1
        # 修改标记
        if entireSet:
            entireSet = False
        elif (alphaPairsChanged == 0):
            entireSet = True
        print("iteration number: %d" % iter)
    return oS.b,oS.alphas

#################################################################################################

# 辅助函数：导入数据
def loadDataSet(filename):
    dataMat = []
    labelMat = []
    fr = open(filename)
    for line in fr.readlines():
        lineArr = line.strip().split('\t')
        dataMat.append([float(lineArr[0]), float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat, labelMat

# 测试函数
def testRbf(k1 = 1.3):
    # 导入训练集
    dataArr,labelArr = loadDataSet('testSetRBF.txt')
    b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', k1)) #C=200 important
    datMat = mat(dataArr)
    labelMat = mat(labelArr).transpose()
    # 取所有的支持向量
    svInd = nonzero(alphas.A > 0)[0]
    sVs = datMat[svInd]
    labelSV = labelMat[svInd]
    print("there are %d Support Vectors" % shape(sVs)[0])
    m,n = shape(datMat)
    # 计算训练集的错误率
    errorCount = 0
    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
        predict = kernelEval.T * multiply(labelSV,alphas[svInd]) + b
        if(sign(predict) != sign(labelArr[i])):
            errorCount += 1
    print("the training error rate is: %f" % (float(errorCount) / m))
    # 导入测试集
    dataArr,labelArr = loadDataSet('testSetRBF2.txt')
    errorCount = 0
    datMat = mat(dataArr)
    m,n = shape(datMat)
    # 计算测试集的错误率
    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
        predict = kernelEval.T * multiply(labelSV,alphas[svInd]) + b
        if(sign(predict)!=sign(labelArr[i])):
            errorCount += 1
    print("the test error rate is: %f" % (float(errorCount)/m))


testRbf()

运行结果：

there are 29 Support Vectors
the training error rate is: 0.130000
the test error rate is: 0.150000

Process finished with exit code 0