系统学习机器学习之特征工程（四）--分箱总结

首先from wiki给出一个标准的连续特征离散化的定义：

在统计和机器学习中，离散化是指将连续属性，特征或变量转换或划分为离散或标称属性/特征/变量/间隔的过程。这在创建概率质量函数时非常有用 - 正式地，在密度估计中。它是一种离散化的形式，也可以是分组，如制作直方图。每当连续数据离散化时，总会存在一定程度的离散化误差。目标是将数量减少到手头的建模目的可忽略不计的水平。

在银行风控模型的建模过程中常常涉及到连续特征的离散化，一般来说比较常见的是使用线性回归、逻辑回归的时候常常会对连续特征进行分箱，在建立分类模型时，常常需要对连续变量离散化，特征离散化后，模型会更稳定，降低了模型过拟合的风险。比如在建立申请评分卡模型时用logsitic作为基模型就需要对连续变量进行离散化，离散化通常采用分箱法。下面来谈谈为什么我们要进行连续特征离散化。

1. 离散特征的增加和减少都很容易，易于模型的快速迭代，比如说我们当前训练集的年龄是20～30岁，假设在20～30之间分了5个箱子离散化然后onehot展开，下一次训练的时候如果出现超过30岁的特征，那么直接增加一列0-1特征用来表示用户是否超过30岁即可；
2. 稀疏向量内积乘法运算速度快，计算结果方便存储，容易扩展，稀疏矩阵可以使用稀疏矩阵的存储方式，比如python中的csr_matrix模块，通过稀疏矩阵的存储方式对原始数据进行了压缩。
3. 离散化后的特征对异常数据有很强的鲁棒性：比如一个特征是年龄>30是1，否则0。如果特征没有离散化，一个异常数据“年龄300岁”会给模型造成很大的干扰；
4. 特征离散化后，模型会更稳定，比如如果对用户年龄离散化，20-30作为一个区间，不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反，所以怎么划分区间是门学问，很多时候涉及到业务知识层面的东西；
5. 特征离散化以后，起到了简化了逻辑回归模型的作用，降低了模型过拟合的风险。 (当使用连续特征时，一个特征对应于一个权重，那么，如果这个特征权重较大，模型就会很依赖于这个特征，这个特征的一个微小变化可能会导致最终结果产生很大的变化，这样子的模型很危险，当遇到新样本的时候很可能因为对这个特征过分敏感而得到错误的分类结果，也就是泛化能力差，容易过拟合。而使用离散特征的时候，一个特征变成了多个，权重也变为多个，那么之前连续特征对模型的影响力就被分散弱化了，从而降低了过拟合的风险。)
6. 离散化在onehot展开之后还可以进行特征交叉，这一系列增大特征维度的方法都可以增强逻辑回归这种线性模型的非线性表达能力，根据计算学习理论的covar定理可得，一般来说特征维度越高则线性可分或线性可拟合的概率越高，当然过拟合的概率也越大。
7. 可以将缺失作为独立的一类带入模型。对于缺失值的处理和类别型特征一样，用-1来代替表示缺失值，把“缺失”也当作一种特征
8. 将所有变量变换到相似的尺度上。

---

最近恰好看到了关于离散化综述的好文，搬运记忆，以后说不定就用上。

https://blog.csdn.net/CalCuLuSearch/article/details/52751218​blog.csdn.net

http://www.go-gddq.com/down/2012-03/12031520159066.pdf​www.go-gddq.com

最优离散化问题已经被证明是一个NP-hard问题

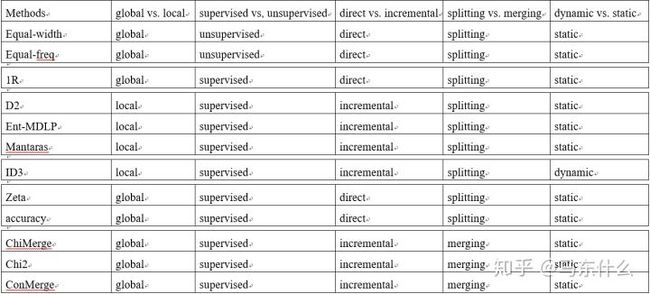
下面详细介绍一下各种各样的离散化方法，特征离散化的方法有很多，不同的分类的标准也很多，有分为有监督和无监督的，动态的和静态的，全局的和局部的，分列式和合并式的，单变量和多变量的以及直接的和增量式的。上面的博客找到了很好的总结图：

 

这种思维导图是真的很好，一目了然，我们常见的等频等宽决策树chimerge均包含在内了。整体来看，特征离散化的方法分为自底向上的merging合并的方案以及从顶向下的分裂的方案，这两种思路下面均有对应的有监督和无监督的解决方案。 

有监督与无监督的离散化方法：

是否使用标签进行离散化（分箱）决定了有监督还是无监督的离散化方法。有监督的离散化方法又分为建立在错误率基础上的、建立在熵值基础上的或者建立在统计信息基础上的。

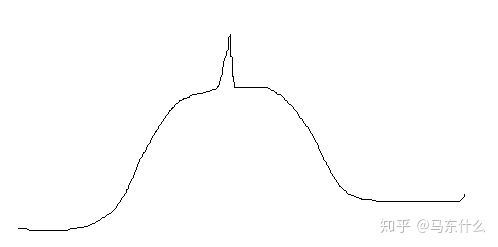
比较常见的有等频、等宽、聚类离散化，这类方案的问题在于对于分布不均匀的数据并不适用，等频和等宽都不能很好的反应“尖头”的数据，除非人工手动干涉，聚类本身对于这类问题的表现也并不稳定，经常可能出现的情况就是“尖头”数据有一部分分到平缓分布的数据里去，导致最终的分箱结果没有代表性：

 

为了克服无监督的离散化方法的这些缺陷，使用类信息来进行离散化的有监督的离散化方法逐渐发展起来。对于分类/回归问题如果要分箱都可以用这种方法，比如下面会提到的动态和静态分箱。

动态与静态分箱

所谓静态分箱就是我们常见的在模型训练前的预分箱处理，而动态分箱是在模型运行的过程中自动完成的，比如决策树实际上在训练的过程中就能够进行自动的分箱操作。

全局与局部(global vs. local)：

另一个分法(dichotomy)是全局与局部。局部离散化方法是在实例空间(instance space/subset of instances)的局部区域(localized region)进行的离散化。然而全局离散化使用了全体实例空间进行离散化。当实例空间的一个区域被用来离散化时局部方法通常与动态离散化方法有关。

这个思路很有意思，个人理解，这种局部转换的场景可能更多应用于存在异常值的情况，直接将异常值替换为某一个并不是那么异常的值，例如：

“尖头”数据明显是很异常的值，在采样验证和模型训练的时候都会产生不利的影响，那么可以将其赋值为附近的常规的数。

自顶向下与自底向上(splitting(top-down) vs. merging(bottom-up))：

离散化方法也可以根据自顶向下与自底向上进行划分。自顶向下方法以一个空的分割点(cut-points/split-points)列表开始，在离散化进程中一直不断的往这个列表中通过splitting intervals添加新的分割点。自底向上以完整的列表开始，该列表用所有的连续特征值作为分割点，在离散化进程中一直不断的给这个列表中通过merging intervals移除的分割点。

直接与增量(direct vs. incremental)：

直接方法同时划分K个间隔的范围(例如equal-width，equal-frequency，K-means)，需要一个额外的输入来决定间隔的个数。增量方法以一个简单的离散化开始，并伴随着改善或者提纯(refinement)过程，需要停止准则来终止下一步的离散化。

典型的离散化过程通常由以下4步组成：
1) sort对离散化的特征的连续值进行排序；
2) evaluate对为了合并的划分的或者邻近的间隔，评估分割点；
3) split or merge通过一些准则，划分或者合并连续值的间隔；
4) stop停止离散化。

排序sorting

对特征的连续值进行降序或者升序排序都可以。如果不关心在离散化时进行排序，那么排序的计算代价将是非常昂贵的。对于所有的特征，排序在离散化开始之前完成，这将是一个全局处理(global treatment)，适用于将整个实例空间离散化。如果排序在过程的每一次迭代时完成，这将是一个局部处理(local treatment)，仅对整个实例空间的一个区域进行离散化。

选择分割点 choosing a cut-point

排序之后，离散化过程接下来的一步是寻找最好的分割点，对连续值的范围进行划分，或者寻找最好的一对邻近的间隔进行合并。一个典型的评价函数用来决定一次划分或者合并与类别标签的关系。文献中提到很多评价函数，诸如：熵测量、统计测量。关于评价函数与它们的应用将在下一小节进行讨论。

划分/合并Splitting/merging

正如我们所知，对自顶向下的方法，间隔是划分；然而对于自底向上的方法，间隔是合并。对于划分，需要评价分割点，选择最好的一个，并将连续值范围划分成两部分。分别对每一部分进行离散化直到满足停止准则。对于合并，评估邻近的间隔，找到最好的间隔进行合并。离散过程一直持续，间隔数随之减少，直到满足停止准则。

停止准则stopping criteria

停止准则是为了终止离散过程。它经常被元数和精度的折中所支配，因为这两个是正互相关的(positively correlated)。我们可以将k作为离散化的结果的元数设置一个上界，事实上，上界k的设置是远小于N的，假设没有特征连续值的副本，停止准则可能是非常简单的，诸如在一开始固定间隔数，或者一个稍微复杂一些的如评价函数。在下一章节描述不同的停止准则。

离散化方法对比comparison of discretization methods

针对不同离散化方法获得的离散化数据，哪一个更好呢？看起来是一个简单的问题，却很难用简单的答案来回答。这是因为不同的方法之间的比较是一个复杂的问题，它依赖于用户在某一个特殊应用的需求。说复杂是因为不同方法的评价可以从多个方面来进行。我们列举了3个重要的维度：(1)总的间隔数，直观的，间隔点越少，离散化结果越好；但是强加于数据呈现是有限的。这导致第二个维度。(2)离散化引起的不一致性的个数。它不应该大于离散化之前原始数据的不一致数。如果最终结果是从数据训练一个分类器，应该考虑另一个观点。(3)预测精度-离散化对预测精度的改善。简言之，我们至少需要三个维度的考虑：简化(simplicity)、一致性(consistency)、精度(accuracy)。理想情况下，最好的离散化结果在这三方面应都有最高的得分。但事实上，它是不可能达到的，或者不需要的。为不同的离散化方法在这三方面提供一个均衡的观点也是本文的目标。

简化(simplicity)使用分割点的总数来定义的。精确度(accuracy)在交叉验证模式下运行分类器可以获得。一致性(consistency)是最小的不一致性计数值，可以通过以下3步计算而来(下面的描述中，模式pattern指没有类别标签的实例)：(1)如果两个实例有着相同的属性值，但是类别标签不一样，则这两个实例是不一致的；例如，如果两个实例是(0 1;0)和(0 1;1)，它们就是不一致的。(2)一个模式的计数值是这个模式出现在数据中的次数减去最大的类别标签数；例如，假设有n个实例与这个模式相匹配，其中label1的个数是c1, label2的个数是c2，label3的个数是c3，其中c1+c2+c3=n。如果c3是这三个中最大的，则该模式的不一致性计数值为(n-c3)。(3)总的不一致性计数是一个特征集合中所有可能的模式的不一致性计数值之和。（这一段没有太深刻的理解和体会其实。。。）

4.离散化框架discretization framework

文献中提到很多离散化方法。正如上面所述的一样，根据不同的维度可以对这些方法进行分类。即：监督与无监督(supervised vs, unsupervised)；动态与静态(dynamic vs. static)；全局与局部(global vs. local)；自顶向下与自底向上(splitting(top-down) vs. merging(bottom-up))；直接与增量(direct vs. incremental)。可以根据这些维度的不同组合来对这些方法进行分组。我们希望构建一个系统的、可扩展的、能覆盖现在所有方法的框架。文献中提到的每一种离散化方法离散化一个特征：或者对连续值划分间隔；或者合并邻近的间隔。划分和合并根据是否使用分类信息可进一步分组成监督与无监督。

鉴于这些方面的考虑，我们提出了层次化框架(hierarchical framework)，如下图所示。

 

通过两种方法：划分和合并，描述了不同的离散化测量(level1)。接着我们考虑了方式是监督还是无监督(level2)。进一步我们将使用相同离散化度量方法的分组在一起(level3)，例如分箱(binning)和熵(entropy)。如下图所示，监督与无监督划分决定了不同的度量方法。因此概念上有用的划分将不再详细讲述。

我们将讨论如下表所示的基于划分和合并的分类方法的现存的不同的度量方式。

在以下两个小节，将选择典型的方法进行深入讨论(in-deep discussion)。它们相关的或者派生的(related or derived)度量方法也会简要涉及。对每一个离散化度量方式，我们主要给出：

(1). 度量方式的定义；

(2). 在离散化方法中的应用；

(3). 使用的停止准则；

(4). 对Iris数据集的离散化结果：每一个属性的分割点；

在小节的最后，出于对比目的，我们给出了所有离散化度量方式的结果列表：不一致性的个数、离散化的分割点。

4.1划分方法splitting method

我们以用于划分离散化方法的通用算法开始。

在离散化过程中划分算法(splitting algorithm)由4步组成，它们是：

(1). 对特征值排序；

(2). 搜索合适的分割点；

(3). 根据分割点划分连续值的范围；

(4). 当满足停止准则的时候停止离散化否则继续；

文献中提到很多划分离散化度量方法：分箱(binning)、熵(entropy)、独立性(dependency)、精确度(accuracy)。

分箱binning

Equal width or frequency

1R

熵entropy

ID3 type

D2

Ent-MDLP

Mantaras distance

独立性dependency

Zeta

精确度accuracy

adaptive quantizer

---

4.2合并方法merging method

我们以采用合并或者自底向上方法的离散化通用算法开始。

在离散化过程中合并算法由4个重要步骤组成，它们是：

(1). 对值进行排序；

(2). 找到最好的两个相邻间隔；

(3). 把这一对合并成一个间隔；

(4). 满足停止条件时终止。

merge合并的方案：

chi-square measure

ChiMerge

chi2

4.3讨论discussion

我们已经回顾了在划分和合并归类情况下的典型离散化方法。大部分方法是基于划分方法的。我们使用Iris数据集作为一个例子展示了不同的离散化方法的结果。两种度量方式(number of inconsistencies and number of cut-points)直觉上的关系是：分割点越多，不一致计数越少。仔细观察表明(closer look)让两个计数值都少可能有一个妥协(middle ground)的方法。因此，我们应该旨在去让两个数值(number of inconsistencies and number of cut-points)都小。我们确实发现对于Iris数据一些方法比其他方法要好：Ent-MDLP是划分方法里边最好的；chi2是合并方法里边最好的。Chi2也表明，通过考虑一定程度的不一致性，在两种度量方式之间达到折中也是可能的。除离散化之外(in addition to)，Chi2也移除了具有一定程度的不一致性的特征。

在section2，我们通过5种不同的维度回顾了监督与无监督(supervised vs, unsupervised)；动态与静态(dynamic vs. static)；全局与局部(global vs. local)；自顶向下与自底向上(splitting(top-down) vs. merging(bottom-up))；直接与增量(direct vs. incremental)的离散化方法。在多维观点(muti-dimensional view)下我们又得到了另外一种类型的分组。如下表所示：

对于上述分箱方法的细致分类

Splitting

1、我们首先来看splitting下的无监督的分箱方法，它是最早期的一种较为简单的分箱方法，包括等频、等距、聚类以及人工根据先验来自定义分箱，除了人工自定义方法根据使用者经验的好坏影响分箱结果的好坏之外，其它三种自动化的分箱方法的优势在于简单好理解，并且无监督的方法不需要引入目标值，但是也都都存在着较大的缺陷：对不均匀的数据不适用，并且对异常值很敏感，先说等宽分箱，如果数据分布极端，两边数据多，中间数据很少，那么很容易出现不少箱子里面没有数据，等频虽然可以保证每个箱子里的样本数量大致相等，但是有可能出现不同箱子之间跨度太大的情况，比如上述出现异常值的情况，可能最终分箱的结果是一部分箱子的区间长度为10，另一部分箱子的区间长度为1000，同样，对于聚类的方法，不均匀样本和异常样本的存在会导致聚类中心的向极端值偏移从而影响分箱结果，这三种分箱方法sklearn都已经做好了感动哭了。

sklearn.preprocessing.KBinsDiscretizer - scikit-learn 0.21.2 documentation​scikit-learn.org

>>> X = [[-2, 1, -4,   -1],
...      [-1, 2, -3, -0.5],
...      [ 0, 3, -2,  0.5],
...      [ 1, 4, -1,    2]]
>>> est = KBinsDiscretizer(n_bins=3, encode='ordinal', strategy='uniform')
>>> est.fit(X)  
KBinsDiscretizer(...)
>>> Xt = est.transform(X)
>>> Xt  
array([[ 0., 0., 0., 0.],
       [ 1., 1., 1., 0.],
       [ 2., 2., 2., 1.],
       [ 2., 2., 2., 2.]])

sklearn的0.21版中的KBinsDiscretizer 目前支持等频、等宽和聚类分箱。

另外还有提到的1R的分箱方案：

上面的方案都是属于无监督分箱，下面我们介绍下有监督分箱

下面用sklearn的api和sklearn的决策树简单做了一个基于cart tree的决策树分箱，实现了sklearn原生的cart tree和lgb以及xgb tree分箱的功能，不知道效果如何。

from sklearn.base import BaseEstimator, TransformerMixin

class supervised_bins_Transformer(BaseEstimator, TransformerMixin):#我们这里写一个分箱的方法
    def __init__(self, task='Classification', method='xgboost_tree'):

        self.task=task
        self.method=method #method 支持4种类型，一种是xgboost tree，一种是lightgbm tree，一种是sklearn tree
        #一种是chimerge 
 

    def fit(self, X=None, y=None):
        if self.method=='xgboost_tree':
            if self.task=='Classification':
                clf=xgb.XGBClassifier(n_estimators=1)
            else:
                clf=xgb.XGBRegressor(n_estimators=1)
            clf.fit(X,y)
        
            
        if self.method=='lightgbm_tree':
            if self.task=='Classification':
                clf=lgb.LGBMClassifier(n_estimators=1)
            else:
                clf=lgb.LGBMRegressor(n_estimators=1)
            clf.fit(X.values.reshape(-1,1),y)
            
        
        if self.method=='sklearn_tree':
            if self.task=='Classification':
                clf=tree.DecisionTreeClassifier()
            else:
                clf=tree.DecisionTreeRegressor()
            clf.fit(X.values.reshape(-1,1),y)
            tree_rules=clf.tree_.threshold
            self.tree_rules=tree_rules[tree_rules!=-2] #sklearn 中的tree用-2判断叶节点，-2不是一个分裂阈值要删除
 
 

 
    def transform(self, X):
        
        return np.digitize(X,self.tree_rules)

Merging

说实话，好多给出的分箱方案我都没听说过，资料也找不到太多，emmm，一般来说一项技术如果市面上的资料太多，大概率是3种可能的结果：1、技术太新；2、技术缺陷太多；3、技术不错但应用太窄价值不高 ，所以我还是挑比较常见的算法来学习吧。。。看一大堆名字都不清楚啥意思的算法我就不浪费时间再去研究了。

https://mp.weixin.qq.com/s?__biz=MzIxNzc1NDgzMw==&mid=2247483991&idx=1&sn=158037a76cb356643a12ea926e827afe&chksm=97f5bfe9a08236ff1d5f9ddd4c604028f7953dda20a4986991faf884fad932a40f5826ff95c0&scene=21#wechat_redirect​mp.weixin.qq.com

https://mp.weixin.qq.com/s?__biz=MzA5Njc1MDA2Ng%3D%3D&idx=1&mid=2651650083&sn=a24381efa404500ae96ccfcc3716a614​mp.weixin.qq.com

关于卡方分布、卡方分箱上面的两个链接介绍的很直观了，这里就总结一下了，前人栽树后人乘凉哈哈哈：

卡方分布(chi-square distribution, χ2-distribution)是概率统计里常用的一种概率分布，也是统计推断里应用最广泛的概率分布之一，在假设检验与置信区间的计算中经常能见到卡方分布的身影。

卡方分布的定义如下：

若k个独立的随机变量Z1, Z2,..., Zk 满足标准正态分布 N(0,1) , 则这k个随机变量的平方和：

为服从自由度为k的卡方分布，记作：

卡方检验即χ2检验是以χ2分布为基础的一种假设检验方法，主要用于分类变量之间的独立性检验。其基本思想是根据样本数据推断总体的分布与期望分布是否有显著性差异，或者推断两个分类变量是否相关或者独立。一般可以设原假设为 ：观察频数与期望频数没有差异，或者两个变量相互独立不相关。

基本思想:对于精确的离散化，相对类频率在一个区间内应当完全一致。因此,如果两个相邻的区间具有非常类似的类分布，则这两个区间可以合并；否则，它们应当保持分开。而低卡方值表明它们具有相似的类分布。
实际应用中，我们先假设原假设成立，计算出卡方的值，卡方表示观察值与理论值间的偏离程度。

卡方值的计算公式为：

其中A为实际频数，E为期望频数。卡方值用于衡量实际值与理论值的差异程度，这也是卡方检验的核心思想。

卡方值包含了以下两个信息：

1.实际值与理论值偏差的绝对大小。
2.差异程度与理论值的相对大小。

上述计算的卡方值服从卡方分布。根据卡方分布，卡方统计量以及自由度，可以确定在原假设成立的情况下获得当前统计量以及更极端情况的概率p。如果p很小，说明观察值与理论值的偏离程度大，应该拒绝原假设。否则不能拒绝原假设。

根据上面连接里给的源代码写了一个sklearn api形式的卡方分箱：

import numpy as np
import pandas as pd
from numba import jit,guvectorize,int64
from scipy.stats import chi2
import xgboost as xgb
import lightgbm as lgb
from sklearn import tree
from sklearn.base import BaseEstimator, TransformerMixin

class Chi2_Bins_Transformer(BaseEstimator,TransformerMixin):
    def __init__(self,target,max_groups=-1,threshold=None,):
        self.max_groups=max_groups
        self.threshold=threshold

        if self.max_groups ==-1:
            if self.threshold is None:
                cls_num = np.unique(target).shape[0]
                self.threshold = chi2.isf(0.05,df= cls_num - 1)  ##通过查表设置卡方阈值
                
                    
    @staticmethod
    def Chi2(arr):
    #计算每行总频数
        R_N = arr.sum(axis=1)   
    #每列总频数
        C_N = arr.sum(axis=0)    
    #总频数
        N = arr.sum()  
    # 计算期望频数 C_i * R_j / N。
        E = np.ones(arr.shape)* C_N / N
        E = (E.T * R_N).T
        square = (arr-E)**2/ E    
    #期望频数为0时，做除数没有意义，不计入卡方值
        square[E==0] = 0  
    #卡方值
        return square.sum()  
        
 


    @staticmethod
#    @guvectorize(["(int64[:,:], float64[:],int64,float64)"], '(m,n),(m),(),()',cache=True, \
#                  nopython=True)
    def ChiMerge(freq,cutoffs,max_groups,threshold):       
        while True:
            minvalue=None
            minidx=None
            for i in range(freq.shape[0]-1):
                v=Chi2_Bins_Transformer.Chi2(freq[i:i+2])
                
                if minvalue is None or minvalue>v:
                    minvalue=v
                    minidx=i
                
            if (max_groups !=-1 and max_groups

本来想用numba来做加速的，发现numba针对于class的局限性确实还是蛮大的，另外numba一般支持numpy的纯数学运算的，对于一些逻辑运算（比如true，false之类的会报错），也就是说我们用numba的nopython模式编译的时候基本要保证函数里面的所有数据（包括临时变量等）都要为number型，总之刚开始用坑还是蛮多的，而且调试很麻烦，另外用object的模式编译真的基本没什么加速有时候反而还会更慢坑爹。比较适合一些小而精简的函数的优化比如：