数据挖掘：银行评分卡制作——数据分箱、WOE、IV的意义

在银行评分卡的项目中，通常都会需要把数据分箱，分箱后并不是对数据进行哑变量处理，而是用WOE值去替换，再放入模型中。
学习的过程中会对这些操作有些疑问，比如，数据分箱有什么意义，WOE和IV值是干什么的？这里对这些数据处理的意义进行一个说明。

数据分箱

数据分箱是把连续型数据分为几组，或者把离散数据中类别较多的，进行重新划分，划分为类别数较少的特征。

数据分箱的意义

1. 把离散特征的类别进行分箱二次分类（比如，中国的所有城市，通过分箱划分为县区市地区等），可以让模型快读迭代。
2. 对于连续特征，分箱会降低数据的噪声影响。分箱后的数据有很强的稳定性。
3. 将连续数据分箱后，进行哑变量或独热编码的处理，每个特征中的每一类别就有了权重，这样相当于为模型引入的非线性，能够提升模型的拟合能力。
   这里可以看到，原来的特征只有x1，哑变量处理后变成xa和xb（类比多项式回归），增强了逻辑回归处理非线性的能力
   

分箱的方法分为有监督和无监督。

• 有监督分箱：卡方分箱，Best-KS分箱（只能二分类）等。
• 无监督分箱：等宽分箱，等频分箱，聚类分箱，最小熵法等。
• 分箱方法介绍

注：连续值的分箱不一定是要分成离散数据，而是一种数据平滑的处理，可以几个数据分在一起，然后取其平均值或中位数，降低数据的噪声。

WOE和IV

将数据离散化后，要想放入逻辑回归模型中，需要对数据进行处理，因为数据中的123是类别不是大小，这个数量关系仅仅表示顺序，他们之间实质性的数值间隔你是不知道的（WOE可以解决这个问题）。而我们一般用的方法是哑变量，或独热编码，将特征中的类别提取出来，设为单独的一个特征。那什么是WOE？

WOE

woe全称是Weight of Evidence，即证据权重。是对原始自变量的一种编码形式。

WOE的两种公式理解

1.坏人的分布减去好人的分布。

2.每个箱中的坏人好人之间的比值 与 整个特征中坏人好人之间的比值 的差异。

WOE越大，以上这两种差异就越大。原始数据中好人，坏人都混在一起，是无法分清的。我们通过分箱的操作，可以把好人坏人尽可能的分割开，而WOE就是衡量分箱后，好人坏人的分割程度的。
从两种角度理解WOE公式

WOE和逻辑回归

逻辑回归的公式为：

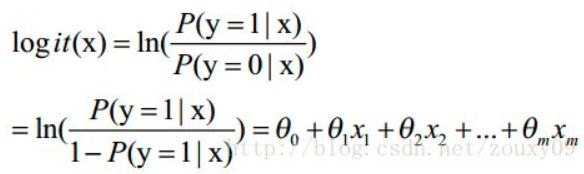
其中，我们可以发现左边的式子跟WOE很像，但WOE是(Badi/BadT)/(Goodi/GoodT)，给定样本后，BadT和GoodT是确定的（样本中的好坏数是一定的），所以影响WOE大小的，只有每组的Badi和Goodi。
把右边的xWOE化（原来是数字123），其实是为了对应左边的公式，让左右两边成一个正比关系。
这样特征中各个组之间的关系由之前的数字123（单个组内的类别），转变为WOE（该特征和标签值结合的一个结果，之前只是一个单纯的组内分组，没有跟标签值扯上关系）能够看出特征中各个类别对标签值的影响大小。
而WOE的公式长成这个样子，也是为了跟逻辑回归相互照应。参照之前的线性回归，系数代表了特征的贡献量。而逻辑回归为了也跟线性回归起到一样的效果，更好地解释特征对模型的贡献度，特别是对离散变量，因此有了WOE。

WOE和哑变量

1.WOE
这里的w就是特征x中各类别的WOE值。δ只是为了后面评分而加的字符。

2.哑变量
dummy变量是比较顺其自然的操作，例如某个自变量m有3种取值分别为m1,m2,m3，那么可以构造两个dummy变量M1、M2：当m取m1时，M1取1而M2取0；当m取m2时，M1取0而M2取1；当m取m3时，M1取0且M2取0。这样，M1和M2的取值就确定了m的取值。之所以不构造M3变量，是基于信息冗余和多重共线性之类的考虑。（构造M3就是独热编码，而非哑变量）
x11对应xa，即样本属于x11的，xa全为1，xb全为0.

3.woe变量的系数都会是正的
x1中坏样本比例高，w11>0，那么w12<0(好样本比例高)。根据上面截图中的公式，可以得到w11与a1之间有关系，因为w11>0，所以a1>0.同理可得到a2.
根据公式，由于x11与xa同号，所以系数必然>0.若是负值，则需要重新分箱。

4.不使用哑变量而使用WOE的原因

1. 无法对自变量的每一个取值计算其信用得分
2. 回归模型筛选变量时可能出现某个自变量被部分地舍弃的情况。

WOE单调性的意义

权重w为常数：个人理解是因为左右两边的ln()，因为有对应关系（x^2 = ax ^2,a=1，为常量），上面也说了，成正比，因此w为常量。

w为常量，所以分子，分母的变化一致，WOE递增时，分子也递增（分子可以理解为判定该样本为坏的概率）。注：这里让WOE的值单调是为了让woe(x)与y之间具备线性的关系，更有助于人们的理解，而不是最开始x和y之间的非线性。

注：若非单调，即转换为WOE后，x与y之间还是非线性关系，则可重新分箱（等频有益于分箱），或手动调整。

WOE的计算案例

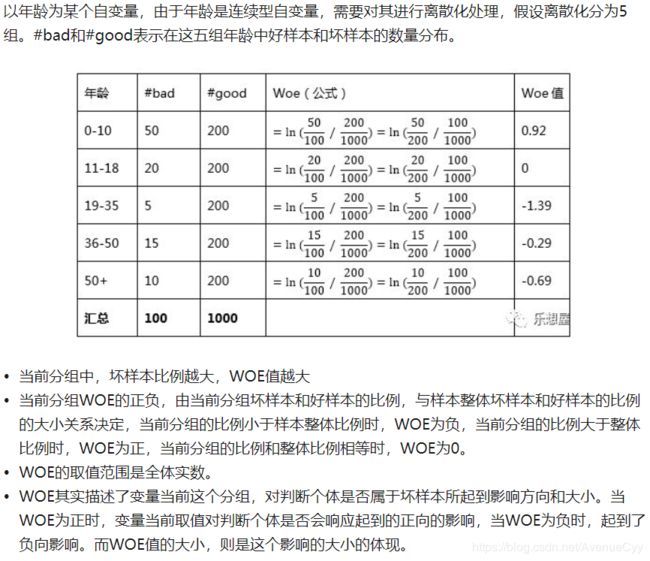
1.WOE公式中是坏的比好的。
2.WOE值的正负，描述了当前这个分组对判断个体（该组内的数据）是否属于坏样本起到了影响方向和大小的作用。

• 正，分组比例大于总体比例，影响方向为正，即向着坏样本，其影响大小为具体数值。
• 负，分组比例小于总体比例，影响方向为负，即向着好样本，其影响大小为具体数值。

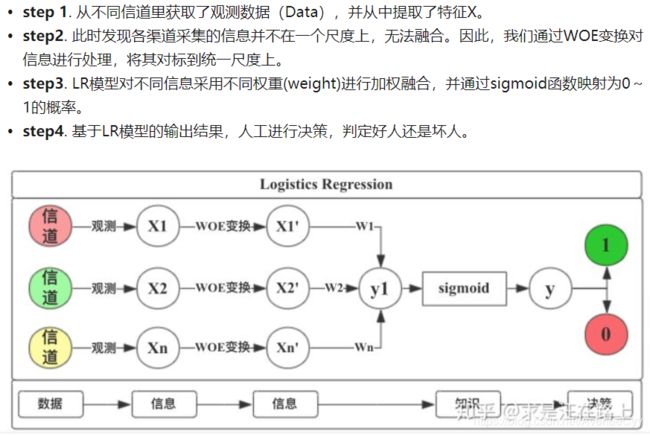
WOE处理流程

WOE转换好处

3.WOE编码之后，自变量其实具备了某种标准化的性质，也就是说，自变量内部的各个取值之间都可以直接进行比较（WOE之间的比较）

注：WOE没有考虑分组中样本占整体样本的比例，如果一个分组的WOE值很高，但是样本数占整体样本数很低，则对变量整体预测的能力会下降。因此，我们还需要计算IV。

IV值

IV（Information Value）即，信息价值。

IV值的意义

IV就是用来衡量自变量的预测能力，把更有利于预测的特征选出来。


为什么IV能用来衡量信息量：
背后的支撑理论是相对熵。IV把预期分布和实际分布具体化为好人分布和坏人分布。IV指标是在从信息熵上比较好人分布和坏人分布之间的差异性。

IV的计算公式

IV的计算基于WOE，可以看成对WOE的加权求和。
对于每一个分组i，能计算出WOEi。对于分组i，也会有一个对应的IV值。

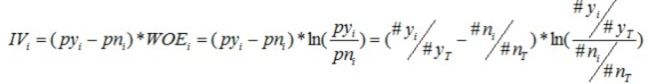
整个变量的IV值，把各分组的IV相加：

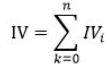
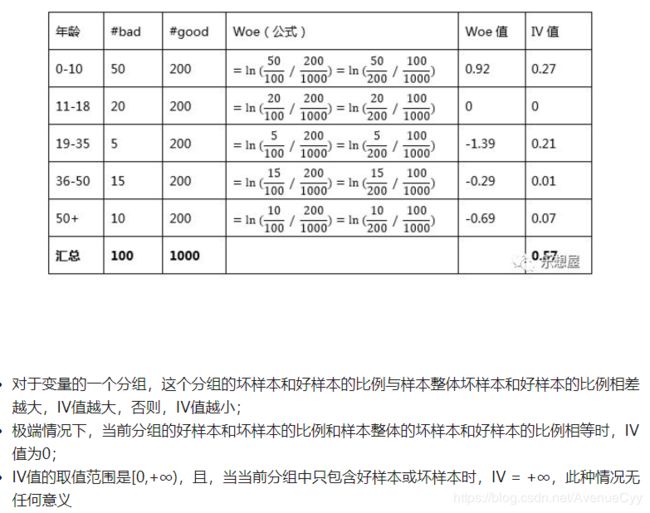
IV的计算案例

衡量IV值对模型的贡献度

WOE和IV值进一步思考

为什么用IV而不是直接用WOE

变量各分组的WOE和IV都隐含着这个分组对目标变量的预测能力这样的意义。那我们为什么不直接用WOE相加或者绝对值相加作为衡量一个变量整体预测能力的指标呢？

1. 当我们衡量一个变量的预测能力时，我们所使用的指标值不应该是负数，否则，说一个变量的预测能力的指标是-2.3，听起来很别扭。
   
   但这个原因并不是最重要的，因为可以加绝对值来限制值为正。
2. 主要原因是乘以(pi-pn)后，体现出了变量当前分组中个体的数量占整体个体数量的比例，对变量预测能力的影响。
   举个例子：
   当变量A取值1时，其响应比例达到了90%，但是我们不能说变量A的预测能力非常强，因为A取1时，响应比例虽然很高，但这个分组的客户数太少了，占的比例太低了。虽然，如果一个客户在A这个变量上取1，那他有90%的响应可能性，但是一个客户变量A取1的可能性本身就非常的低（可以看到取0的样本量非常多，因此客户在A上取1的概率就很小，而这一切都是因为这个分组的样本量太少了，所以，对于样本整体来说，变量的预测能力并没有那么强）
   
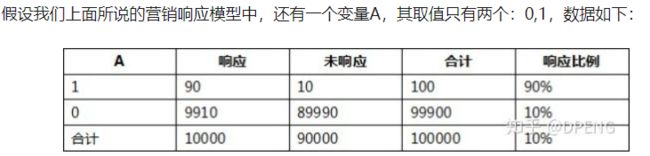
   从这个表我们可以看到，变量取1时，响应比达到90%，对应的WOE很高，但对应的IV却很低，原因就在于IV在WOE的前面乘以了一个系数(pi-pn)，而这个系数很好的考虑了这个分组中样本占整体样本的比例，比例越低，这个分组对变量整体预测能力的贡献越低。相反，如果直接用WOE的绝对值加和，会得到一个很高的指标，这是不合理的。
   
   

IV的极端情况及处理方式

IV依赖WOE，并且IV是一个很好的衡量自变量对目标变量影响程度的指标。但是，使用过程中应该注意一个问题：变量的任何分组中，不应该出现响应数=0或非响应数=0的情况。（每个分箱中，都必须有正负样本）

由上述问题我们可以看到，使用IV其实有一个缺点，就是不能自动处理变量的分组中出现响应比例为0或100%的情况。那么，遇到响应比例为0或者100%的情况，我们应该怎么做呢？建议如下：

所以，一般在编写分箱函数的时候，都会考虑分箱中正负样本数。

参考文献

https://blog.csdn.net/pylady/article/details/78882220
https://zhuanlan.zhihu.com/p/29316085
https://zhuanlan.zhihu.com/p/80134853
https://zhuanlan.zhihu.com/p/111459123
https://zhuanlan.zhihu.com/p/89071633