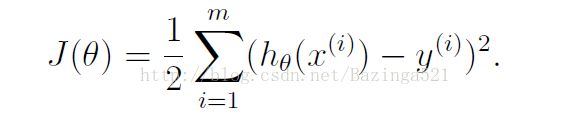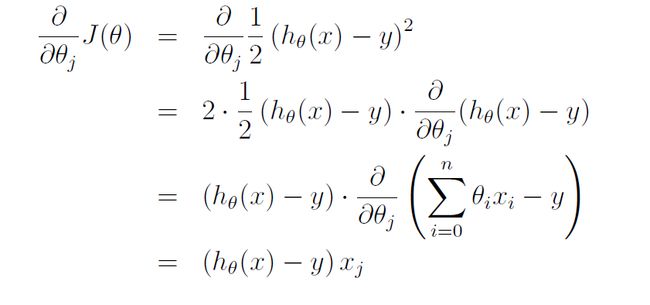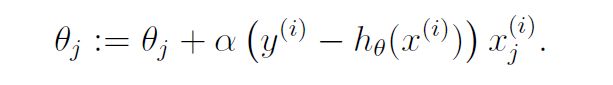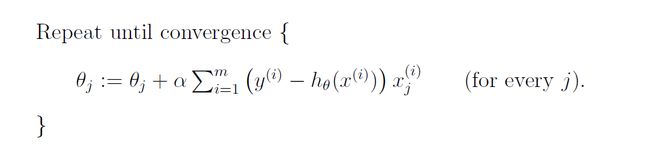斯坦福机器学习3：线性回归、梯度下降和正规方程组的matlab实现

斯坦福机器学习3：线性回归、梯度下降和正规方程组的matlab实现

以一个最简单的一元线性回归为例，给定一个数据集，（x,y）一个x值对应一个y，假设x是面积，y是房价

一元线性回归就是在一个x，y坐标系中回归出一条直线，也就是

h(x)=θ₀+θ₁x

h(x)是预测值，

我们定义目标函数，也就是我们要优化的函数

然后用梯度下降法来更新参数，更新的规则为θ-α*(J(θ))’

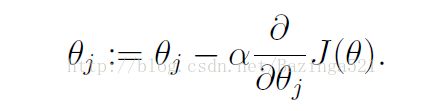
对于一个多维的函数h(x)=θ₀+θ₁x₁+θ₂x₂每一个θ对应一个x，θ₀没有x对应，所以在建立参数矩阵时需要在第一列加上一列0和θ₀相乘，这样h(x)=θ₀+θ₁x₁+θ₂x₂₌θ^TX，其中X的行是数据的数量，列是3.

所以θ₁的更新时候的X_j就是X(I,j)

批梯度下降每次θ更新的时候都需要把所有的数据都计算一遍梯度，然后求和

用matlab代码实现为

 for i=1:m
        gra0=gra0+(thita(1)+thita(2)*x(i)-y(i))*1;
        gra1=gra1+(thita(1)+thita(2)*x(i)-y(i))*x(i)
    end
    thita(1)=thita(1)-alf*gra0
    thita(2)=thita(2)-alf*gra1

将上述代码多循环几遍就是一元线性回归，全部代码为

clc, clear all, close all
x=[23.80,27.60,31.60,32.40,33.70,34.90,43.20,52.80,63.80,73.40];
y=[41.4,51.8,61.70,67.90,68.70,77.50,95.90,137.40,155.0,175.0];
thita=[-16,10];   %调初始点对结果影响很大
alf=0.000001;
dis=0;
m=length(y);
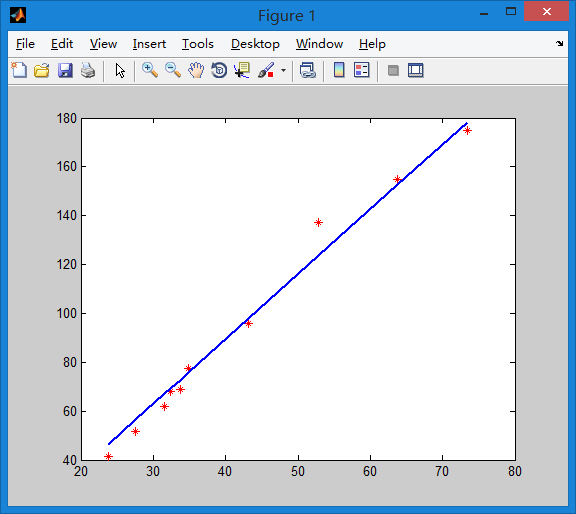
plot(x,y,'r*');
hold on
for re=1:100000
    gra0=0;
    gra1=0;
    for i=1:m
        gra0=gra0+(thita(1)+thita(2)*x(i)-y(i))*1;
        gra1=gra1+(thita(1)+thita(2)*x(i)-y(i))*x(i)
    end
    thita(1)=thita(1)-alf*gra0
    thita(2)=thita(2)-alf*gra1
end
for i=1:m
    dis=dis+(thita(1)+thita(2)*x(i)-y(i))^2;
end
h=thita(1)+thita(2)*x
plot(x,h,'linewidth',2);

结果如下

只需要多设置几个参数就可以变成多元线性回归，也就是房价跟卧室的数量，跟面积，跟位置等多个变量有关。

多元线性回归的代码如下：

thita=[0,0,0,0];
x=[10931.64 1672.00 514.83;11718.01 1757.00 566.17;12883.46 1950.00 630.73;13249.80 1959.00 748.89;14867.49 1971.00 901.24;16682.82 1970.00 1175.46;18645.03 2718.20 1246.86;20667.91 2774.20 1275.59;23623.35 2931.00 1307.53];
y=[3422 3565 3866 4134 5118 5855 6842 7196 10320];
a=0.0001;
for re=1:50
dis=0;
for i=1:9
    dis=dis+((thita(1)+thita(2)*x(i,1)+thita(3)*x(i,2)+thita(4)*x(i,3))-y(i))^2;
end
gra1=0;
gra2=0;
gra3=0;
gra4=0;
for i=1:9
    gra1=gra1+((thita(1)+thita(2)*x(i,1)+thita(3)*x(i,2)+thita(4)*x(i,3))-y(i))*1;
    gra2=gra2+((thita(1)+thita(2)*x(i,1)+thita(3)*x(i,2)+thita(4)*x(i,3))-y(i))*x(i,1);
    gra3=gra3+((thita(1)+thita(2)*x(i,1)+thita(3)*x(i,2)+thita(4)*x(i,3))-y(i))*x(i,2);
    gra4=gra4+((thita(1)+thita(2)*x(i,1)+thita(3)*x(i,2)+thita(4)*x(i,3))-y(i))*x(i,3);
end
thita(1)=thita(1)-a*gra1;
thita(2)=thita(2)-a*gra2;
thita(3)=thita(3)-a*gra3;
thita(4)=thita(4)-a*gra4

end
anti=round(thita(1)+thita(2)*(10931.64)+thita(3)*1672+thita(4)*(514.83))

可以看到如果参数再多的话程序写出来就会越来越麻烦。所以有正规方程组法。视频中具体推导的过程如下：

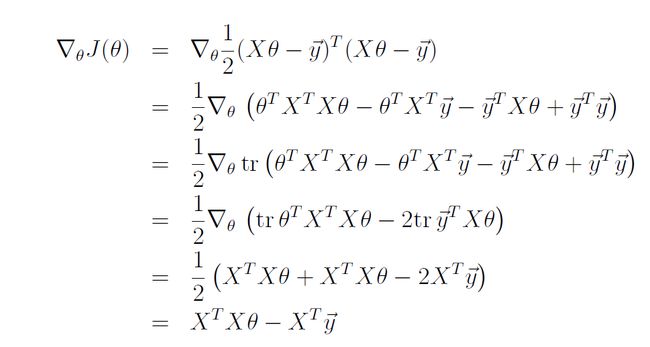
梯度等于0的点就是最优点

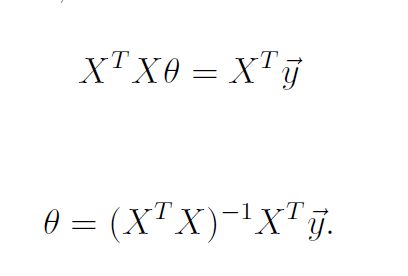
所以根据向量运算我们可以直接求出最优θ的值。

Matlab实现也就变得很方便，代码如下：

x=[1 10931.64 1672.00 514.83;1 11718.01 1757.00 566.17;1 12883.46 1950.00 630.73;1 13249.80 1959.00 748.89;1 14867.49 1971.00 901.24;1 16682.82 1970.00 1175.46;1 18645.03 2718.20 1246.86;1 20667.91 2774.20 1275.59;1 23623.35 2931.00 1307.53];
y=[3422; 3565; 3866; 4134 ;5118 ;5855; 6842 ;7196 ;10320];
thita=[0;0;0;0;];
thita=inv(x'*x)*x'*y;
h=[1 16682.82 1970.00 1175.46]*thita;
format long g
h

最后三行代码是测试了其中一行特征向量输入值，发现拟合出来的公式计算这一行向量的值不相等，但是很接近，说明拟合结果挺好