位运算及其骚操作

概念

计算机中的数在内存中都是以二进制形式进行存储的，用位运算就是直接对整数在内存中的二进制位进行操作，因此其执行效率非常高，在程序中尽量使用位运算进行操作，这会大大提高程序的性能。

补码

数值有正负之分，二进制中最高位为0代表正，为 1 则代表负
例子：（这种表示被称作原码）
0000 1100 对应的十进制为 12
1000 1100 对应的十进制为 -12
但新的问题出现了，原本二进制的最高位始终为 0，为了表示正负又多出了 1，在执行运算时就会出错。举个例子，1 + (-2) 的二进制运算如下：

    0000 0001
+ 1000 0010
=  1000 0011
= -3

为了解决这个问题，就搞出了补码的概念。补码是为了让负数变成能够加的正数，所以
负数的补码 = 负数的绝对值取反 + 1，

-1 的绝对值 1
= 0000 0001 # 1 的二进制原码
= 1111 1110 # 原码取反
= 1111 1111 # +1 后得到补码

正数的补码与原码相同，不需要额外运算。也可以说，补码的出现就是为了解决负数运算时的符号问题。

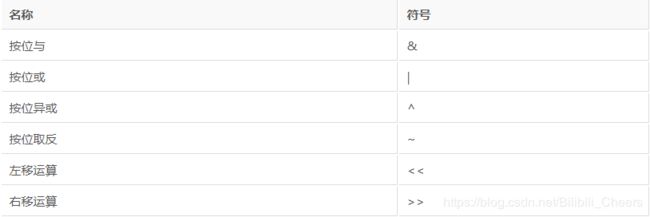
运算符

左移运算：<<

将数对应的二进位全部向左移动若干位，高位丢弃，低位补 0
左移相当于乘. 左移一位相当于乘2¹;左移两位相当于乘2²;左移三位相当于乘2³。
数字 5 左移 4 位 = 5 (2) ⁴

5 << 4
= 0000 0101 << 4
= 0101 0000 # 高位丢弃，低位补 0
= 80

左移运算的规律： x << n = x(2)ⁿ

右移运算：>>

将数对应的二进位全部向右移动若干位。对于左边的空位，如果是正数则补 0，负数可能补 0 或 1
右移相当于整除. 右移一位相当于除以2;右移两位相当于除以4;右移三位相当于除以8。
数字 80 右移 4 位 = 80/2⁴

80 >> 4
= 0101 0000 >> 4
= 0000 0101 # 正数补0，负数补1
= 5

右移运算的规律： x >> n = x / (2)ⁿ

按位与：&

两数对应的二进制位相与，当对应的二进制位均为 1 时，结果位为 1，否则结果位为 0。

5&8 = 0

0000 0101
&
0000 1000
=
0000 0000

按位或：|

两数对应的二进制位相或，只要对应的二进制位中有 1，结果位为 1，否则结果位为 0。

3|7 = 7

0000 0011
|
0000 0111
=
0000 0111

按位异或：^

两数对应的二进制位相异或，当对应的二进制位值不同时，结果位为 1，否则结果位为 0。

12^7 = 11

0000 1100
^
0000 0111
=
0000 1011

按位取反：~

公式：~x = - ( x + 1)
二进制数的每一个位上面的 0 换成 1，1 换成 0。按位取反的运算符为 ~

对数字 9 进行按位取反运算

～0000 1001
= 0000 1001 # 补码，正数补码即原码
= 1111 1010 # 取反
= -10

-20 按位取反的过程如下：

～0001 0100
= 1110 1100 # 补码
= 0001 0011 # 取反
= 19

应用

1. 判断数字奇偶

通常，我们会通过取余来判断数字是奇数还是偶数。例如判断 101 的奇偶用的方法是：

if 101 & 1:
    print('奇数')
else:
    print('偶数')

这是因为奇数的二进制最低位始终为 1，而偶数的二进制最低为始终为 0。 所以，无论任何奇数与 1 即 0000 0001 相与得到的都是 1，任何偶数与其相与得到的都是 0。

2. 变量交换

//位与操作
void swap(int &a, int &b) {
  a ^= b;
  b ^= a;
  a ^= b;
}

3. 运算 + - * /

/// 

/// 加法
/// 
/// 
/// 
/// 
public static int Add(int a, int b)
{        
    if (b == 0)// 假如进位为0
    {
        return a;
    }
    // 获得求和位
    int s = a ^ b;
    // 获得进位,然后需要向做移动一位表示进位
    int c = ((a & b) << 1);
    return Add(s, c);
}
/// 

/// 减法函数 (就是使用加法来做的，只是说加了一个负数)
/// 
/// 
/// 
/// 
public static int Subtract(int a, int b)
{
    return Add(a, Adverse(b));
}

/// 

/// 乘法
/// 
/// 
/// 
/// 
public static int Multiply(int a, int b)
{
    bool flag = true;
    // 如果相乘为正数，flag为false
    if (GetSign(a) == GetSign(b))
        flag = false;
    // 将a取正数
    a = ToPositive(a);
    b = ToPositive(b);
    int re = 0;

    while (b != 0)
    {
        // 相加
        re = Add(re, a);
        // b进行次数减一
        b = Subtract(b, 1);
    }
    // 假如结果是负数，则进行取反
    if (flag)
        re = Adverse(re);
    return re;
}

/// 

/// 除法 a/b
/// 
/// 
/// 
/// 
public static int Divide(int a, int b)
{
    bool flag = true;
    // 如果相除为正数，flag为false
    if (GetSign(a) == GetSign(b))
        flag = false;
    // 将a取正数
    a = ToPositive(a);
    b = ToPositive(b);
    int re = 0;
    int i = 31;
    while (i >= 0)
    {
        // 如果够减
        // 不用(b<
        if ((a >> i) >= b)
        {
            // re代表结果
            re = Add(re, 1 << i);
            a = Subtract(a, (b << i));
        }
        // i减一
        i = Subtract(i, 1);
    }
    // 假如结果是负数
    if (flag)
        re = Adverse(re);
    return re;
}

/// 

/// 取得相反数
/// 
/// 
/// 
private static int Adverse(int a)
{
    return Add(~a, 1);
}

/// 

/// 负数返回-1，正数返回0
/// 
/// 
/// 
private static int GetSign(int i)
{
    return (i >> 31);
}

/// 

/// 如果为负数，则进行取反 
/// 
/// 
/// 
private static int ToPositive(int a)
{
    if (a >> 31 == -1)
        // 进行取反
        return Add(~a, 1);
    else
        return a;
}

4. 异或筛去出现偶数次的数

异或运算可以筛选出偶数次的数，因为相同的数 异或运算后为 0

5. 位操作交换符号

交换符号将正数变成负数，负数变成正数

int reversal(int a) {
  return ~a + 1;
}

整数取反加1，正好变成其对应的负数(补码表示)；负数取反加一，则变为其原码，即正数

6. 位操作求绝对值

整数的绝对值是其本身，负数的绝对值正好可以对其进行取反加一求得，即我们首先判断其符号位（整数右移 31 位得到 0，负数右移 31 位得到 -1,即 0xffffffff），然后根据符号进行相应的操作

int abs(int a) {
  int i = a >> 31;
  return i == 0 ? a : (~a + 1);
}

7. 位操作进行高低位交换

给定一个 16 位的无符号整数，将其高 8 位与低 8 位进行交换，求出交换后的值，如：
34520的二进制表示：
10000110 11011000
将其高8位与低8位进行交换，得到一个新的二进制数：
11011000 10000110
其十进制为55430

unsigned short a = 34520;
a = (a >> 8) | (a << 8);