动手学深度学习PyTorch版课程笔记

作者：DennisShaw

---

Task03：

---

过拟合、欠拟合及其解决方案

• 训练误差（training error）：模型在训练数据集上表现出的误差

• 泛化误差（generalization error）：模型在任意一个测试数据样本上表现出的误差的期望
  计算误差使用模型中的损失函数来计算，例如之前的线性回归的平方损失函数和softmax回归的交叉熵损失函数

机器学习模型应关注降低泛化误差

模型的选择：在选择模型中，不应只依赖训练数据选择模型。
解决方法：

1. 可设置预留在训练集与测试集之外的验证集，或给定训练集中随机选取一小部分作为验证集来从训练误差中估计泛化误差。
2. 使用K折交叉验证，把原始训练数据集分割成K个不重合的子数据集，做K次模型训练和验证，用一个子数据集验证模型，并使用其他K-1个子数据集来训练模型。

过拟合与欠拟合：

• 欠拟合：模型无法得到较低的训练误差
• 过拟合：模型的训练误差远小于它在测试数据集上的误差

两种影响拟合问题的因素：

• 模型复杂度：模型复杂度与误差的关系
  
• 训练数据集大小：训练数据集中样本数过少，特别是比模型参数数量（按元素计）更少时，过拟合更容易发生。泛化误差不会随训练数据集里样本数量增加而增大。

权重衰减：等价于$L_2$范数正则化，正则化通过为模型损失函数添加惩罚项使学出的模型参数值较小，可应对过拟合。
在模型原损失函数基础上添加$L_2$范数惩罚项，从而得到训练所需要最小化的函数。$L_2$范数惩罚项指的是模型权重参数每个元素的平方和与一个正的常数的乘积。
丢弃法：当对隐藏层使用丢弃法时，该层的隐藏单元将有一定概率被丢弃掉。在训练模型时起到正则化的作用，并可以用来应对过拟合。

总结：

解决方法：
欠拟合：1、加大模型复杂程度 2、增加更多的特征，使输入数据具有更强的表达能力 3、调整参数和超参数 4、降低正则化约束
过拟合：1、增加训练数据 2、使用正则化约束（权重衰减） 3、减少特征数 4、减小模型复杂程度 5、调整参数和超参数
6、神经网络中Dropout（丢弃法） 7、提前结束训练

课后练习：（错题分析）

无

---

梯度消失、梯度爆炸

在深度模型中，有关数值稳定性就是梯度消失问题与梯度爆炸问题。
当神经网络的层数较多时，模型的数值稳定性容易变差
随机初始化模型参数：
若将每个隐藏单元的参数都初始化为相等的值，无论隐藏单元有多少，隐藏层本质上只有1个隐藏单元在发挥作用。所以通常将神经网络的模型参数，特别是权重参数，进行随机初始化。
PyTorch中nn.Module的模块参数都采取了较为合理的初始化策略，一般情况无需我们考虑。
Xavier随机初始化：Xavier随机初始化将使该层中权重参数的每个元素都随机采样于均匀分布，主要考虑到，模型参数初始化后，每层输出的方差不该受该层输入个数影响，且每层梯度的方差也不该受该层输出个数影响。
环境因素：
协变量偏移：输入的分布可能随时间而改变，但是标记函数，即条件分布P（y∣x）不会改变，这种协变量变化是因为问题的根源在于特征分布的变化（即协变量的变化）。
标签偏移：当我们认为导致偏移的是标签P（y）上的边缘分布的变化，但类条件分布是不变的P（x∣y）时，就会出现相反的问题。当我们期望标签偏移和协变量偏移保持时，使用来自标签偏移假设的方法通常是有利的。
概念偏移：即标签本身的定义发生变化的情况。
Kaggle 房价预测实战：

课后练习：（错题分析）

如果数据量足够的情况下，确保训练数据集和测试集中的数据取自同一个数据集，可以防止协变量偏移和标签偏移是正确的。如果数据量很少，少到测试集中存在训练集中未包含的标签，就会发生标签偏移。

---

循环神经网络进阶

RNN存在的问题：梯度较容易出现衰减或爆炸（BPTT）
解决方法：采用门控循环神经网络，捕捉时间序列中时间步距离较大的依赖关系，如GRU、LSTM。
GRU当中的重置门主要捕捉短期依赖、更新门主要捕捉长期依赖。
LSTM中：
遗忘门:控制上一时间步的记忆细胞
输入门:控制当前时间步的输入
输出门:控制从记忆细胞到隐藏状态
记忆细胞：⼀种特殊的隐藏状态的信息的流动
深度循环神经网络
双向循环神经网络：有效捕捉上下文信息，前向的隐藏层参数$H_t$与后向的隐藏层参数$H_t$用concat进行连结

课后练习：（错题分析）

无

---

Task04

---

机器翻译及相关技术

数据预处理：

1. 读取数据，数据预处理，处理编码问题与无效字符串
2. 分词
3. 建立词典
4. 对数据进行padding操作。
5. 制作数据生成器

Seq2seq模型搭建：
一般使用Encoder-Decoder结构，先转化为中间语义表示再进行输出

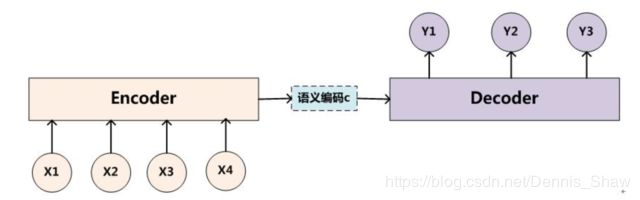
课后练习：（错题分析）

训练时decoder每个单元的输入单词为序列中的第n个单词，输出为第n+1个单词。
每个batch训练时encoder和decoder都有固定长度的输入。

---

注意力机制与Seq2seq模型

在seq2seq模型中，解码器只能隐式地从编码器的最终状态中选择相应的信息。然而，注意力机制可以将这种选择过程显式地建模。
Attention 是一种通用的带权池化方法，输入由两部分构成：询问（query） 和 键值对（key-value pairs）

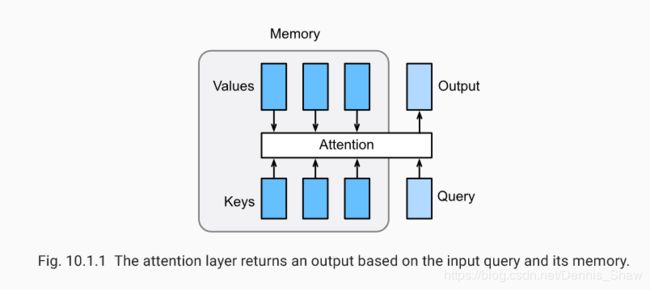
Attention layer得到输出与value的维度一致
对于一个query来说，attention layer 会与每一个key计算注意力分数并进行权重的归一化，输出的向量$o$则是value的加权求和，而每个key计算的权重与value一一对应。
为了计算输出，我们首先假设有一个函数$a$用于计算query和key的相似性，然后可以计算所有的 attention scores
使用 softmax函数 获得注意力权重
最终的输出就是value的加权求和

不同的attetion layer的区别在于Score函数的选择，在本节的其余部分，我们将讨论两个常用的注意层 Dot-product Attention 和 Multilayer Perceptron Attention:
点积注意力 Dot-product Attention:假设query和keys有相同的维度,通过计算query和key转置的乘积来计算attention score，通常还会除去$\sqrt{d}$减少计算出来的score对维度的依赖性。
$$\alpha (q,k)=⟨q,k⟩/\sqrt{d}$$
多层感知机注意力 Multilayer Perceptron Attention:在多层感知器中，我们首先将 query and keys 投影到${\mathbb{R}}^h$.我们将可以学习的参数做如下映射$W_k\in {\mathbb{R}}^{h\times d_k}$, $W_q\in {\mathbb{R}}^{h\times d_q}$ , $v\in {\mathbb{R}}^h$。 将score函数定义$$\alpha (k,q)=v^T\tanh (W_{k}k+W_{q}q)$$
然后将key 和 value 在特征的维度上合并（concatenate），然后送至 a single hidden layer perceptron 这层中 hidden layer 为 ℎ 且输出的size为 1 .隐层激活函数为tanh，无偏置。

尽管MLPAttention包含一个额外的MLP模型，但如果给定相同的输入和相同的键，我们将获得与DotProductAttention相同的输出
总结

• 注意力层显式地选择相关的信息。
• 注意层的内存由键-值对组成，因此它的输出接近于键类似于查询的值。

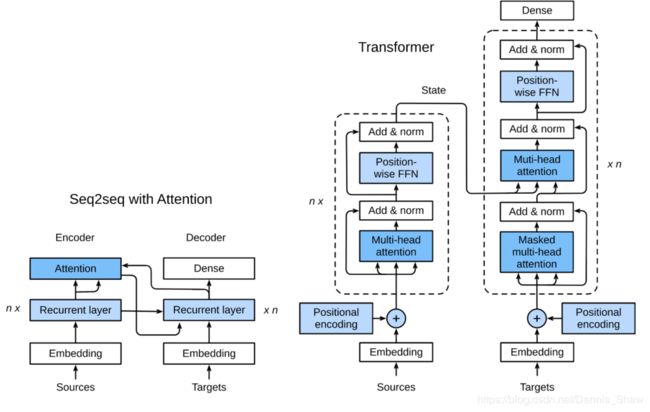
引入注意力机制的Seq2seq模型：
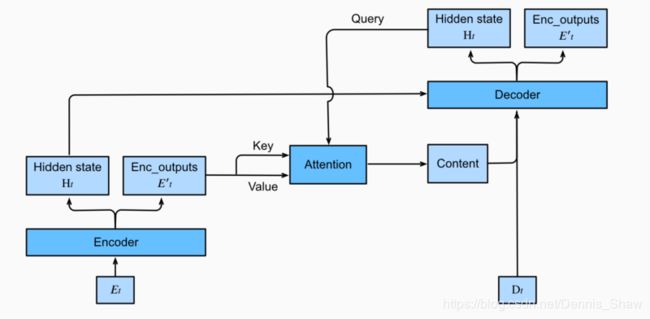
下图展示encoding 和decoding的模型结构，在时间步为t的时候。此刻attention layer保存着encodering看到的所有信息——即encoding的每一步输出。在decoding阶段，解码器的时刻的隐藏状态被当作query，encoder的每个时间步的hidden states作为key和value进行attention聚合. Attetion model的输出当作成上下文信息context vector，并与解码器输入$D_t$拼接起来一起送到解码器：

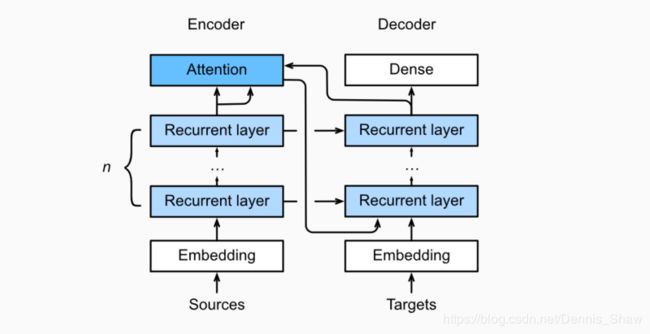
具有注意机制的seq2seq模型中层结构:

课后练习：（错题分析）

在Dot-product Attention中，key与query维度需要一致，在MLP Attention中则不需要，在MLP Attention中key与query维度可以不等。
注意力掩码可以用来解决一组变长序列的编码问题。
seq2seq模型的预测需人为设定终止条件，设定最长序列长度或者输出[EOS]结束符号，若不加以限制则可能生成无穷长度序列。
解码器RNN仍由编码器最后一个时间步的隐藏状态初始化。
注意力机制本身有高效的并行性，但引入注意力并不能改变seq2seq内部RNN的迭代机制，因此无法加速。
有效长度不同的输入会导致 Attention Mask 不同，屏蔽掉无效位置后进行attention，会导致不同的输出。参考代码Dot-Product Attention的测试部分。

---

Transformer

• CNNs 易于并行化，却不适合捕捉变长序列内的依赖关系。
• RNNs 适合捕捉长距离变长序列的依赖，但是却难以实现并行化处理序列。

使用注意力机制设计的Transformer模型结合了CNN与RNN的优势。
利用attention机制实现了并行化捕捉序列依赖，并且同时处理序列的每个位置的tokens，上述优势使得Transformer模型在性能优异的同时大大减少了训练时间。

Transformer与Encoder-Decoder结构的不同之处在于：

1. Transformer blocks：将seq2seq模型重的循环网络替换为了Transformer Blocks，该模块包含一个多头注意力层（Multi-head Attention Layers）以及两个position-wise feed-forward networks（FFN）。对于解码器来说，另一个多头注意力层被用于接受编码器的隐藏状态。
2. Add and norm：多头注意力层和前馈网络的输出被送到两个“add and norm”层进行处理，该层包含残差结构以及层归一化。
3. Position encoding：由于自注意力层并没有区分元素的顺序，所以一个位置编码层被用于向序列元素里添加位置信息。

基于位置的前馈网络：
Transformer 模块另一个非常重要的部分就是基于位置的前馈网络（FFN），它接受一个形状为（batch_size，seq_length, feature_size）的三维张量。Position-wise FFN由两个全连接层组成，他们作用在最后一维上。因为序列的每个位置的状态都会被单独地更新，所以我们称他为position-wise，这等效于一个1x1的卷积。

课后练习：（错题分析）

解码器部分均只需进行的前向传播在训练过程1次，预测过程要进行句子长度次。
自注意力模块理论上可以捕捉任意距离的依赖关系。
解码器部分在预测过程中不需要使用 Attention Mask。

在MultiHeadAttention模块中：
$h$个注意力头中，每个的参数量为$3d^2$
，最后的输出层形状为$hd\times d$，所以参数量共为$4h{d}^2$

层归一化有利于加快收敛，减少训练时间成本。
层归一化对一个中间层的所有神经元进行归一化。
层归一化的效果不会受到batch大小的影响。

批归一化（Batch Normalization）才是对每个神经元的输入数据以mini-batch为单位进行汇总

---

Task05

---

卷积神经网络基础

二维卷积层：二维互相关（cross-correlation）运算的输入是一个二维输入数组和一个二维核（kernel）数组，输出也是一个二维数组，其中核数组通常称为卷积核或过滤器（filter）。卷积核的尺寸通常小于输入数组，卷积核在输入数组上滑动，在每个位置上，卷积核与该位置处的输入子数组按元素相乘并求和，得到输出数组中相应位置的元素。图1展示了一个互相关运算的例子，阴影部分分别是输入的第一个计算区域、核数组以及对应的输出。

二维卷积层将输入和卷积核做互相关运算，并加上一个标量偏置来得到输出。卷积层的模型参数包括卷积核和标量偏置。

二维卷积层输出的二维数组可以看作是输入在空间维度（宽和高）上某一级的表征，也叫特征图（feature map）。影响元素 x 的前向计算的所有可能输入区域（可能大于输入的实际尺寸）叫做 x 的感受野（receptive field）。

填充和步幅：填充（padding）是指在输入高和宽的两侧填充元素（通常是0元素），图2里我们在原输入高和宽的两侧分别添加了值为0的元素。
如果原输入的高和宽是 $n_h$ 和 $n_w$ ，卷积核的高和宽是 $k_h$ 和 $k_w$ ，在高的两侧一共填充 $p_h$ 行，在宽的两侧一共填充 $p_w$列，则输出形状为$$(n_h+p_h-k_h+1)\times (n_w+p_w-k_w+1)$$
在互相关运算中，卷积核在输入数组上滑动，每次滑动的行数与列数即是步幅（stride）。此前我们使用的步幅都是1，图3展示了在高上步幅为3、在宽上步幅为2的二维互相关运算。
一般来说，当高上步幅为 $s_h$ ，宽上步幅为 $s_w$ 时，输出形状为：$$\lfloor (n_h+p_h-k_h+s_h)/s_h\rfloor \times \lfloor (n_w+p_w-k_w+s_w)/s_w\rfloor$$

课后练习：（错题分析）

---

leNet

使用全连接层的局限性：

• 图像在同一列邻近的像素在这个向量中可能相距较远。它们构成的模式可能难以被模型识别。
• 对于大尺寸的输入图像，使用全连接层容易导致模型过大。

使用卷积层的优势：

• 卷积层保留输入形状。
• 卷积层通过滑动窗口将同一卷积核与不同位置的输入重复计算，从而避免参数尺寸过大。

卷积层块里的基本单位是卷积层后接平均池化层：卷积层用来识别图像里的空间模式，如线条和物体局部，之后的平均池化层则用来降低卷积层对位置的敏感性。

卷积层块由两个这样的基本单位重复堆叠构成。在卷积层块中，每个卷积层都使用的窗口，并在输出上使用sigmoid激活函数。第一个卷积层输出通道数为6，第二个卷积层输出通道数则增加到16。

全连接层块含3个全连接层。它们的输出个数分别是120、84和10，其中10为输出的类别个数。
卷积神经网络就是含卷积层的网络。 LeNet交替使用卷积层和最大池化层后接全连接层来进行图像分类。

课后练习：（错题分析）

---

卷积神经网络进阶

Alexnet:
首次证明了学习到的特征可以超越⼿⼯设计的特征，从而⼀举打破计算机视觉研究的前状。
特征：

• 8层变换，其中有5层卷积和2层全连接隐藏层，以及1个全连接输出层。
• 将sigmoid激活函数改成了更加简单的ReLU激活函数。
• 用Dropout来控制全连接层的模型复杂度。
• 引入数据增强，如翻转、裁剪和颜色变化，从而进一步扩大数据集来缓解过拟合。

VGG：通过重复使⽤简单的基础块来构建深度模型。
Block:数个相同的填充为1、窗口形状为3x3的卷积层,接上一个步幅为2、窗口形状为2x2的最大池化层。
卷积层保持输入的高和宽不变，而池化层则对其减半。

NiN：串联多个由卷积层和“全连接”层构成的小⽹络来构建⼀个深层⽹络。
⽤了输出通道数等于标签类别数的NiN块，然后使⽤全局平均池化层对每个通道中所有元素求平均并直接⽤于分类。

GoogLeNet:

• 由Inception基础块组成。
• Inception块相当于⼀个有4条线路的⼦⽹络。它通过不同窗口形状的卷积层和最⼤池化层来并⾏抽取信息，并使⽤1×1卷积层减少通道数从而降低模型复杂度。
• 可以⾃定义的超参数是每个层的输出通道数，我们以此来控制模型复杂度。

课后练习：（错题分析）