数据结构与算法Python版之北大慕课笔记（五）

一、图Graph

1. 图的基础知识

• 图Graph是比树更为一般的结构，也是由节点和边构成的，实际上树是一种具有特殊性质的图。

• 顶点Vertex(也称“节点Node”)是图的基本组成部分，顶点具有名称标识Key，也可以携带数据项payload。

• 边Edge(也称“弧Arc”)，作为2个顶点之间关系的表示，边连接两个顶点；边可以是无向或者有向的，相应的图称作“无向图”和“有向图”。

• 权重Weight，为了表达从一个顶点到另一个顶点的代价，可以给边赋权。例如公交网络中两个站点之间的距离、通行时间和票价都可以作为权重。

  

2. 图的定义

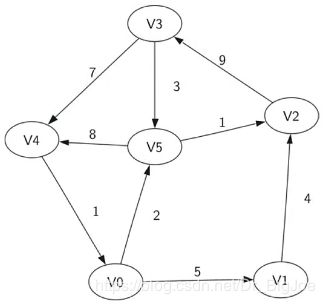
• 一个图G可以定义为G = (V,E)，其中V是顶点的集合，E是边的集合，E中的每条边e = (v, w)，v和w都是V中的顶点；如果是赋权图，则可以在e中添加权重分量子图：V和E的子集。
• 路径Path，图中的路径，是由边依次连接起来的顶点序列；无权路径的长度为边的数量；带权路径的长度为所有边权重的和。
• 圈Cycle，圈是首尾顶点相同的路径。如果有向图不存在任何圈，则称作“有向无圈图 directed acyclic graph: DAG”。如果一个问题能表示成DAG，就可以用图算法很好地解决。

二、ADT Graph

ADT Graph的实现方法有两种主要形式：邻接矩阵adjacency matrix；邻接表adjacency list，两种方法各有优劣，需要在不同应用中加以选择。

1. 邻接矩阵

• 矩阵的每行和每列都代表图中的顶点。

• 如果两个顶点之间有边相连，设定行列值。无权边则将矩阵分量有就标注为1，没有就标注为0；带权边则将权重保存为矩阵分量值。

  

• 邻接矩阵实现法的优点是简单，可以很容易得到顶点是如何相连的。

• 但如果图中的边数很少则效率低下，成为稀疏sparse矩阵。而大多数问题所对应的图都是稀疏的，边远远少于|v|^2 这个量级。

2. 邻接列表

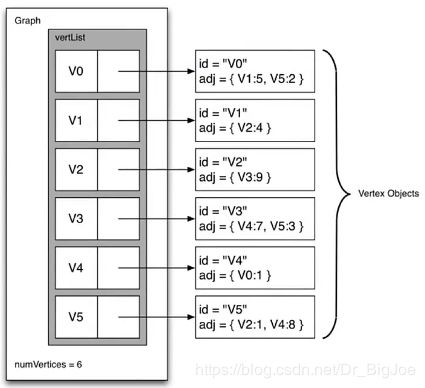
• 邻接列表可以成为稀疏图的更高效实现方案。维护一个包含所有顶点的主列表(master list)，主列表中的每个顶点，再关联一个与自身有边连接的所有顶点的列表。

• 邻接列表法的存储空间紧凑高效，很容易获得顶点所连接的所有顶点，以及连接边的信息。
  

3. ADT Graph的实现

• 顶点Vertex类：Vertex包含了顶点信息，以及顶点连接边信息。

  class Vertex:
      def __init__(self, key):
          self.id = key
          self.connectedTo = {}
  
      def addNeighbor(self, nbr, weight=0):
          self.connectedTo[nbr] = weight  # nbr是顶点对象的key
  
      def __str__(self):
          return str(self.id) + 'connectedTo:' + str([x.id for x in self.connectedTo])
  
      def getConnections(self):
          return self.connectedTo.keys()
  
      def getId(self):
          return self.id
  
      def getWeight(self, nbr):
          return self.connectedTo[nbr]
  

• 图Graph类：Graph保存了包含所有顶点的主表。

  class Graph:
      def __init__(self):
          self.verList = {}
          self.numVertices = 0
  
      def addVertex(self, key):  # 新加顶点
          self.numVertices = self.numVertices + 1
          newVertex = Vertex(key)
          self.verList[key] = newVertex
          return newVertex
  
      def getVertex(self, n):  # 通过key查找顶点
          if n in self.verList:
              return self.verList[n]
          else:
              return None
  
      def __contains__(self, n):
          return n in self.verList
  
      def addEdge(self, f, t, cost=0):
          if f not in self.verList:
              nv = self.addVertex(f)  # 不存在的顶点先添加
          if t not in self.verList:
              nv = self.addVertex(t)
          self.verList[f].addNeighbor(self.verList[t], cost) # 调用起始顶点的方法添加临街边
  
      def getVertices(self):
          return self.verList.keys()
  
      def __iter__(self):
          return iter(self.verList.values())
  

三、图的应用

1. 词梯Word Ladder问题

• 由爱丽丝漫游奇境的作者Lewis Carroll在1878年所发明的单词游戏。
• 从一个单词演变为另一个单词，其中的过程可以经过多个中间单词，要求是相邻两个单词之间差异只能是1个字母。如FOOL变为SAGE：FOOL >> POOL >> POLL >> POLE >> PALE >> SALE >> SAGE
• 我们的目标是找到最短的单词变换序列，采用图来解决这个问题的步骤如下：将可能的单词之间的演变关系表达为图，采用广度优先搜索BFS，来搜寻从开始单词到结束单词之间的所有有效路径，选择其中最快到达目标单词的路径。

构建单词关系图：

• 首先是如何将大量的单词集放到图中，将单词作为顶点的标识key，如果两个单词之间仅相差1个字母，就在它们之间设一条边。

  

• 下图是从FOOL到SAGE的词梯解，所用的图是无向图，边没有权重，FOOL到SAGE的每条路径都是一个解。

  

• 单词关系图可以通过不同的算法来构建（以4个字母的单词表为例），首先是将所有单词作为顶点加入图中，再设法建立顶点之间的边。

• 建立边的最直接算法，是对每个顶点(单词)，与其它所有单词进行比较，如果相差仅1个字母，则建立一条边。时间复杂度是0(n^2)，对于所有4个字母的5110个单词，需要超过2600万次比较。

• 改进的算法是创建大量的桶，每个桶可以存放若干单词，通标记是去掉1个字母，通配符“_”占空的单词。

• 所有匹配标记的单词都放到这个桶里，所有单词就位后，再在同一个桶的单词之间建立边即可。

  

• 对于所有4个字母的5110个单词建立的单词关系图总计有53286条边，仅仅达到矩阵单元数量的0.2%，因此单词关系图是一个非常稀疏的图。

代码实现：

def buildGraph(wordFile):
    d = {}
    g = Graph()
    wfile = open(wordFile,'r')
    for line in wfile:
        word = line[:-1]
        for i in range(len(word)):  # 4字母单词可属于4个桶
            bucket = word[:i] + '_' + word[i+1:]
            if bucket in d:
                d[bucket].append(word)
            else:
                d[bucket] = [word]
    for bucket in d.keys():  # 同一个桶的单词之间建立边
        for word1 in d[bucket]:
            for word2 in d[bucket]:
                if word1 != word2:
                    g.addEdge(word1,word2)
    return g

实现广度优先搜索：

• BFS是搜索图的最简单算法之一，也是其它一些重要的图算法的基础。

• 给定图G，以及开始搜索的起始顶点s。BFS搜索所有从s可到达顶点的边，而且在达到更远的距离k+1的顶点之前，BFS会找到全部距离为k的顶点。可以想象为以s为根，构建一棵树的过程，从顶部向下逐步增加层次。广度优先搜索能保证在增加层次之前，添加了所有兄弟节点到树中。

• 为了跟踪顶点的加入过程，并避免重复顶点，要为顶点增加3个属性。

  1. 距离distance：从起始顶点到此顶点路径长度；
  2. 前驱顶点predecessor：可反向追溯到起点；
  3. 颜色color：标识了此顶点是尚未发现(白色)、已经发现(灰色)、还是已经完成探索(黑色)。

• 还需要一个队列queue来对已发现的顶点进行排列，决定下一个要探索的顶点(队首顶点)。

• 从起始顶点s开始，作为刚发现的顶点，标注为灰色，距离为0，前驱为None，加入队列，接下来是个循环迭代过程：从队首取出一个顶点作为当前顶点；遍历当前顶点的邻接顶点，如果是尚未发现的白色顶点，则将其颜色改为灰色(已发现)，距离增加1，前驱顶点为当前顶点，加入到队列中；遍历完成后，将当前顶点设置为黑色(已探索过)，循环回到步骤1的队首取当前顶点。

  

• 在以FOOL为起始顶点，遍历了所有顶点，并为每个顶点着色，赋距离和前驱之后，既可以通过一个回途追溯函数来确定FOOL到任何单词顶点的最短词梯。

代码实现：

# BFS代码：
def bfs(g,start):
    start.setDistance(0)
    start.setPred(None)
    vertQueue = Queue()
    vertQueue.enqueue(start)
    while (vertQueue.size() > 0):
        currentVert = vertQueue.dequeue()  # 取队首作为当前顶点
        for nbr in currentVert.getConnections():  # 遍历邻接顶点
            if (nbr.getColor() == 'white'):
                nbr.setColor('gray')
                nbr.setDistance(currentVert.getDistance()+1)
                nbr.setPred(currentVert)
                vertQueue.enqueue(nbr)
            currentVert.setColor('black')  # 当前顶点设为黑色

def traverse(y):
    x = y
    while (x.getPred()):
        print(x.getId())
        x = x.getPred()
    print(x.getId())

广度优先搜索算法分析：

• BFS算法主体是两个循环的嵌套，while循环对每个顶点访问一次，所以是O(|V|)，而嵌套在while中的for，由于每条边只有在其起始顶点u出队的时候才会被检查一次，而每个顶点最多出队一次，所以边最多被检查1次，一共是0(|E|)，综合起来BFS的时间复杂度为0(|V|+|E|)。
• 词梯问题还包括两个部分算法：建立BFS树之后，回溯顶点到起始顶点的过程，最多为0(|V|)；创建单词关系图也需要时间，最多为O(|V|^2)。

2. 骑士周游问题

在一个国际象棋棋盘上，一个棋子“马”(骑士)按照马走日的规则，从一个格子出发，要走遍所有棋盘格恰好一次。把一个这样的走棋序列称为一次“周游”。

• 在8*8的国际象棋棋盘上，合格的周游数量有1.305*10^35这么多，采用图搜索算法，是解决骑士周游问题最容易理解和编程的方案之一。

• 解决方案分为两步：首先将合法走棋次序表示为一个图；采用图搜索算法搜寻一个长度为(行×列-1)的路径，路径上包含每个顶点恰一次。

• 将棋盘和走棋步骤构建为图的思路：将棋盘格作为顶点，按照马走日规则的走棋步骤作为连接边，建立每一个棋盘格的所有合法走棋步骤能够到达的棋盘格关系图。

  

• 最后生成的8×8棋盘骑士周游图具有336条边，相比起全连接的4096条边，仅8.2%，还是稀疏图。

骑士周游算法实现：

• 用于解决骑士周游问题的图搜索算法是深度优先搜索(Depth First Search)。

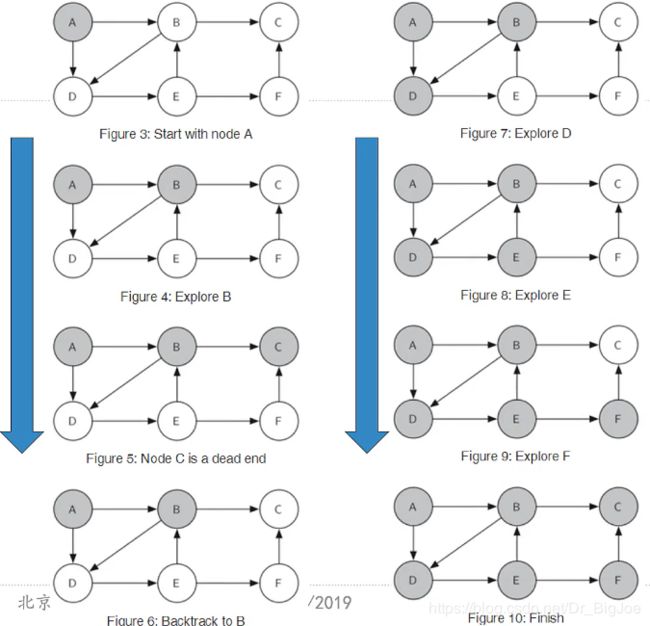
• 相比前述的广度优先搜索逐层建立搜索树的特点，深度优先搜索是沿着树的单支尽量深入向下搜索，如果到无法继续的程度还未找到问题解，就回溯到上一层再搜索下一支。

• 深度优先搜索解决骑士周游的关键思路：如果沿着单支深入搜索到无法继续(所有合法移动都已经被走过了)时，路径长度还没有达到预定值(8×8棋盘为63)，那么就清除颜色标记，返回到上一层，换一个分支继续深入搜索。

• 引入一个栈来记录路径，并实施返回上一层的回溯操作。

  

• 骑士周游问题的其中一个解：

  

骑士周游问题代码实现：

def genLegalMoves(x,y,bdSize):
    newMoves = []
    moveOffsets = [(-1,-2),(-1,2),(-2,-1),(-2,1),  # 马走日8个格子
                   (1,-2),(1,2),(2,-1),(2,1)]
    for i in moveOffsets:
        newX = x + i[0]
        newY = y + i[1]
        if legalCoord(newX,bdSize) and legalCoord(newY,bdSize):
            newMoves.append((newX,newY))
    return newMoves

def legalCoord(x,bdSize):
    if x >= 0 and x < bdSize:  # 确认不会走出棋盘
        return True
    else:
        return False

def knightGraph(bdSize):
    ktGraph = Graph()
    for row in range(bdSize):  # 遍历每个格子
        for col in range(bdSize):
            nodeId = posToNodeId(row,col,bdSize)
            newPositions = genLegalMoves(row,col,bdSize)  # 单步合法走棋
            for e in newPositions:
                nid = posToNodeId(e[0],e[1],bdSize)
                ktGraph.addEdge(nodeId,nid)  # 添加边及顶点
        return ktGraph

def posToNodeId(row,col,bdSize):
    return row*bdSize + col

def knightTour(n,path,u,limit): # n层次，path路径，u当前顶点，limit搜索总深度
    u.setColor('gray')
    path.append(u)  # 当前顶点加入路径
    if n < limit:
        nbrList = list(u.getConnections())  # 对所有合法移动逐一深入
        i = 0
        done = False
        while i < len(nbrList) and not done:
            if nbrList[i].getColor() == 'white':  # 选择白色未经过的顶点深入
                done = knightTour(n+1,path,nbrList[i],limit) # 层次加1，递归深入
            i = i + 1
        if not done:  # 无法完成总深度，回溯，试本层下一个节点
            path.pop()
            u.setColor('white')
    else:
        done = True
    return done

骑士周游算法分析：

• 上述算法的性能高度依赖于棋盘大小，目前实现的算法，其复杂度为O(k^n)，其中，n是棋盘格数目。这是一个指数时间复杂度的算法，其搜索过程表现为一个层次为n的树。

骑士周游算法改进：

• 修改遍历下一格的次序，将u的合法移动目标棋盘格排序为：具有最少合法移动目标的格子优先搜索。
• 采用先验知识来改进算法性能的做法，称作为“启发式规则heuristic”。启发式规则经常用于人工智能领域；可以有效地减小搜索范围、更快达到目标等；如棋类程序算法，会预先存入棋谱，布阵口诀，高手习惯等启发式规则，能够在最短时间内从海量的棋局落子点搜索树中定位最佳落子。

改进代码：

# 骑士周游算法改进代码：
def orderByAvail(n):
    resList = []
    for v in n.getConnections():
        if v.getColor() == 'white':
            c = 0
            for w in v.getConnections():
                if w.getColor() == 'white':
                    c = c + 1
                resList.append((c,v))
    resList.sort(key=lambda x: x[0])
    return [y[1] for y in resList]

• 骑士周游问题是一种特殊的对图进行深度优先搜索，其目的是建立一个没有分支的最深的深度优先树，表现为一条线性的包含所有节点的退化树。

3. 通用的深度优先搜索

• 一般的深度优先搜索目标是在图上进行尽量深的搜索，连接尽量多的顶点，必要时可以进行分支(创建了树)，有时候深度优先搜索会创建多棵树，称为“深度优先森林”。
• 深度优先搜索同样要用到顶点的前驱属性，来构建树或森林。另外要设置“发现时间”和“结束时间”属性。前者是在第几步访问到这个顶点(设置灰色)，后者是在第几步完成了此顶点探索(设置黑色)。

代码实现：

# BFS采用队列存储待访问顶点
# DFS通过递归调用，隐式使用了栈

from pythonds.graphs import Graph
class DFSGraph(Graph):
    def __init__(self):
        super().__init__()
        self.time = 0

    def dfs(self):
        for aVertex in self:
            aVertex.setColor('white')  # 颜色初始化
            aVertex.setPred(-1)
        for aVertex in self:
            if aVertex.getColor() == 'white':
                self.dfsvisit(aVertex)  # 如果还有未包括的顶点，则建森林

    def dfsvisit(self,startVertex):
        startVertex.setColor('gray')
        self.time += 1  # 算法的步数
        startVertex.setDiscovery(self.time)
        for nextVertex in startVertex.getConnections():
            if nextVertex.getColor() == 'white':
                nextVertex.setPred(startVertex)
                self.dfsvisit(nextVertex)  # 深度优先递归访问
        startVertex.setColor('black')  # 节点探索完毕，设为黑色
        self.time += 1
        startVertex.setFinish(self.time)

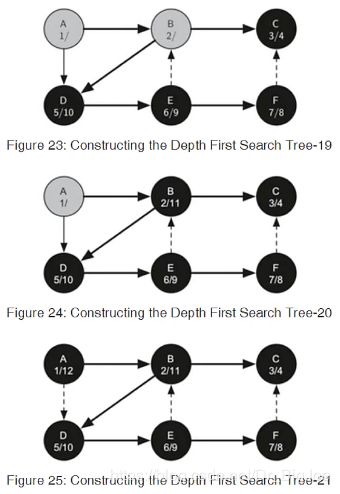
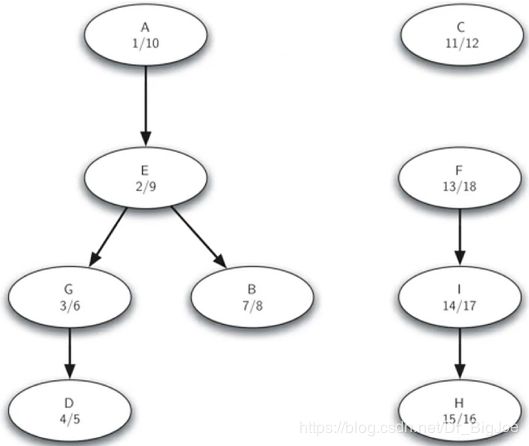
通用的深度优先搜索算法：示例

通用的深度优先搜索算法分析：

• DFS构建的树，其顶点的发现时间和结束时间属性，具有类似括号的性质。即一个顶点的发现时间总小于所有子顶点的发现时间，而结束时间则大于所有子顶点结束时间，比子顶点更早被发现，更晚被结束探索。
• DFS运行时间同样也包括了两方面：dfs函数中有两个循环，每个都是|V|次，所以是O(|V|)，而dfsvisit函数中的循环则是对当前顶点所连接的顶点进行，而且仅有在顶点为白色的情况下才进行递归调用，所以对每条边来说只会运行一步，所以是O(|E|)，加起来就是和BFS一样的O(|V|+|E|)。

4. 拓扑排序Topological Sort

• 很多问题都可转化为图，利用图算法解决。

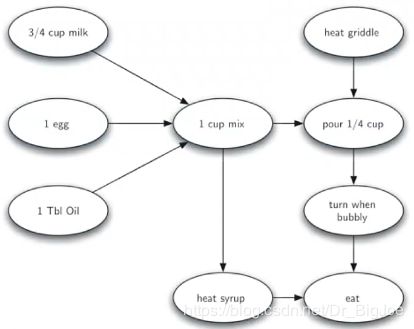
• 例如早餐吃薄煎饼的过程，以动作为起点，以先后次序为有向边。

  

• 问题是对整个过程而言，如果一个人独自做，所有动作的先后次序是什么？

• 从工作流程图得到工作次序排列的算法，称为拓扑排序。拓扑排序处理一个DAG，输出顶点的线性序列，使得两个顶点v, w，如果G中有(v, w)边，在线性序列中v就出现在w之前。

• 拓扑排序广泛应用在依赖事件的排期上，还可以用在项目管理、数据库查询优化和矩阵乘法的次序优化上。

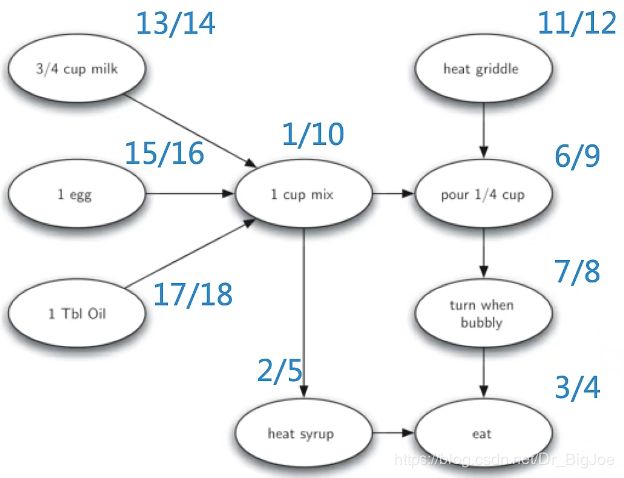
• 拓扑排序可以采用DFS很好地实现：将工作流程建立为图，工作项是节点，依赖关系是有向边，工作流程图一定是个DAG图，否则有循环依赖，对DAG图调用DFS算法，以得到每个顶点的结束时间。按照每个顶点的结束时间从大到小排序，输出这个次序下的顶点列表。

起点从3/4 cup milk开始：

起点从1 cup mix开始：

5. 强连通分支

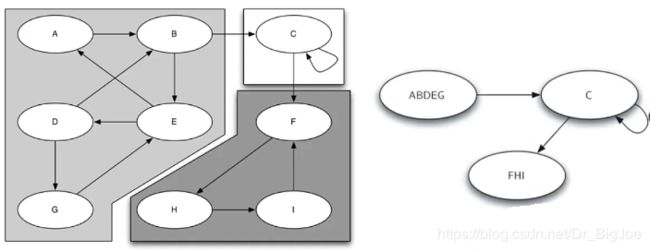
• 在图中发现高度聚集节点群的算法，即寻找“强连通分支Strongly Connected Components”算法。

• 强连通分支，定义为图G的一个子集C，C中的任意两个顶点v,w之间都有路径来回，即(v,w) (w,v)都是C的路径，而且C是具有这样性质的最大子集。

• 下图是具有3个强连通分支的9顶点有向图，一旦找到强连通分支，可以据此对图的顶点进行分类，并对图进行简化。
  

• 在用深度优先搜索来发现强连通分支之前，先熟悉一个概念：Transposition转置。一个有向图G的转置G^T，定义为将图G的所有边的顶点交换次序，如将(v,w)转换为(w,v)。可以观察到图和转置图在强连通分支的数量和划分上，是相同的。
  

强连通分支算法：Kosaraju算法思路

• 首先，对图G调用DFS算法，为每个顶点计算结束时间；
• 然后，将图G进行转置，得到G^T，再对G^T调用DFS算法，但在dfs函数中，对每个顶点的搜索循环里，要以顶点的结束时间倒序的顺序来搜索。
• 最后，深度优先森林中的每一棵树就是一个强连通分支。

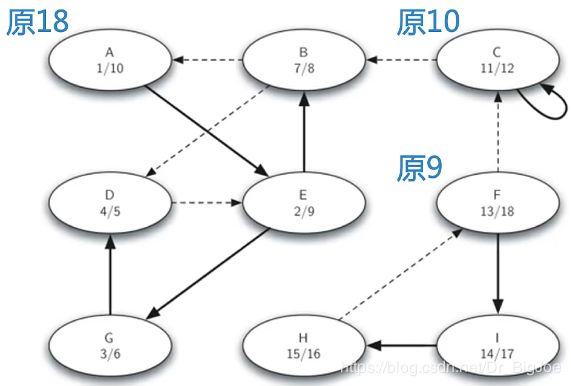
Kosaraju算法实例：第一趟DFS

Kosaraju算法实例：转置后第二趟DFS

Kosaraju算法实例：结果

6. 最短路径问题

• 解决信息在路由器网络中选择传播速度最快路径的问题，可转变为在带权图上最短路径的问题。
• 这个问题与广度优先搜索BFS算法解决的词梯问题相似，只是在边上增加了权重，如果所有权重相等，还是还原到词梯问题。
• 解决带权最短路径问题的经典算法是以发明者命名的Dijkstra算法。这是一个迭代算法，得出从一个顶点到其余所有顶点的最短路径，很接近于广度优先搜索算法BFS的结果。
• 具体实现上，在顶点Vertex类中的成员dist用于记录从开始顶点到本顶点的最短带权路径长度(权重之和)，算法对图中的每个顶点迭代一次。
• 顶点的访问次序由一个优先队列来控制，队列中作为优先级的是顶点的dist属性。
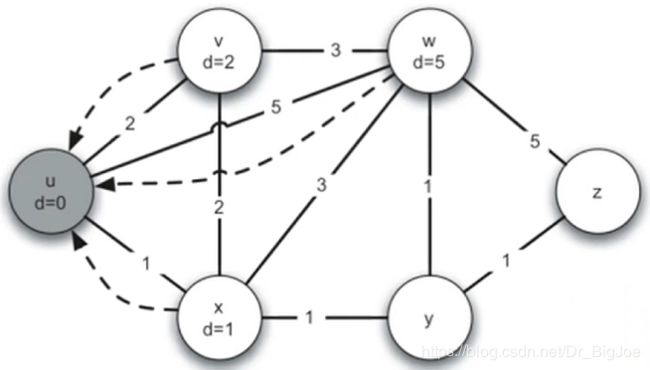
• 最初，只有开始顶点dist设为0，而其他所有顶点dist设为sys.maxsize(最大整数)，全部加入优先队列。
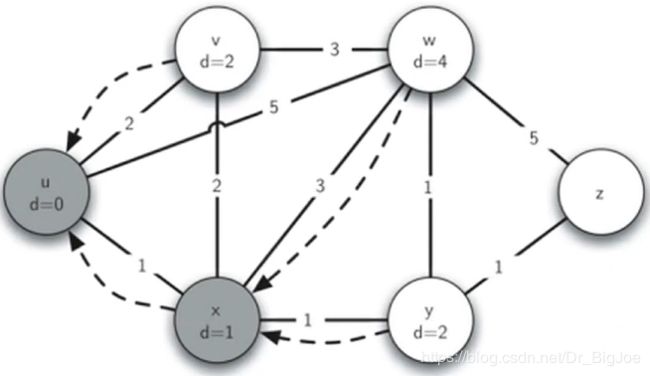
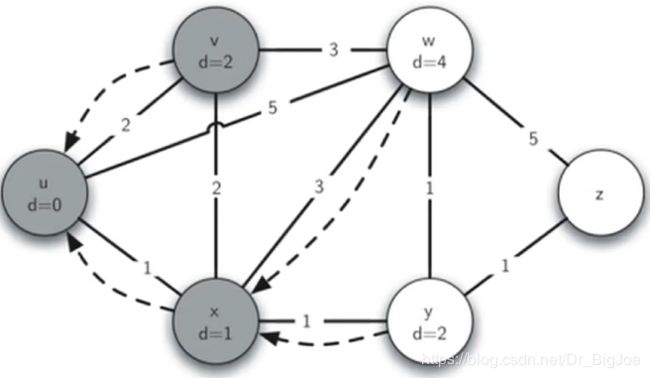
• 随着队列中每个最低dist顶点率先出队，并计算它与邻接顶点的权重，会引起其它顶点dist的减小和修改，引起堆重排。并根据更新后的dist优先级再依次出队。

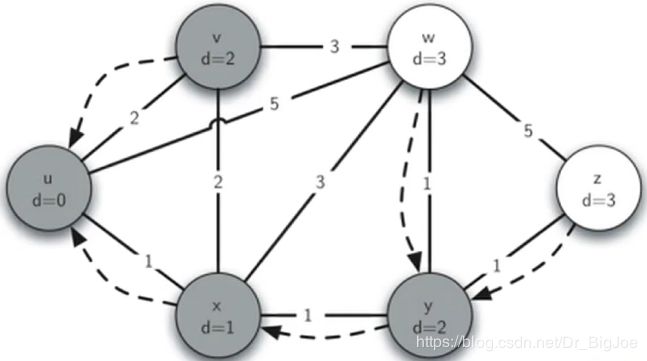
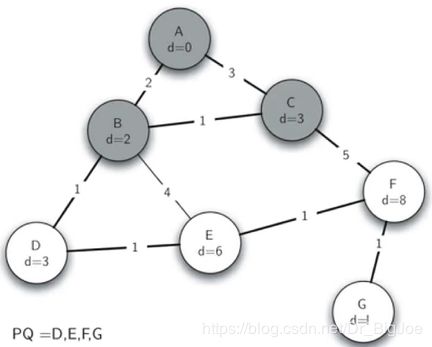
最短路径问题：Dijkstra算法实例

代码实现：

from pythonds.graphs import PriorityQueue,Graph,Vertex
def dijkstra(aGraph,start):
    pq = PriorityQueue()
    start.setDistance(0)
    pq.buildHeap([(v.getDistance(),v) for v in aGraph]) # 对所有顶点建堆，形成优先队列
    while not pq.isEmpty():
        currentVert = pq.delMin()  # 优先队列出队
        for nextVert in currentVert.getConnections():
            newDist = currentVert.getDistance() + currentVert.getWeight(nextVert)
            if newDist < nextVert.getDistance(): # 修改出队顶点所邻接顶点的dist，并逐个重排队列
                nextVert.setDistance(newDist)
                nextVert.setPred(currentVert)
                pq.decreaseKey(nextVert,newDist)

需要注意的是，dijkstra算法只能处理大于0的权重，如果图中出现负数权重，则算法会陷入无限循环。虽然dijkstra散发完美解决了带权图的最短路径问题，但实际上Internet的路由器中采用的是其它算法。

最短路径问题：dijkstra算法分析

• 首先，将所有顶点加入优先队列并建堆，时间复杂度为O(|V|)；
• 其次，每个顶点仅出队1次，每次delMin花费O(log|V|)，一共就是O(|V|log|V|)；
• 另外，每个边关联到的顶点会做一次decreaseKey操作(O(log|V|))，一共是O(|E|log|V|)；
• 上面三个加在一起，数量级就是O((|V|+|E|)log|V|)。

7. 最小生成树

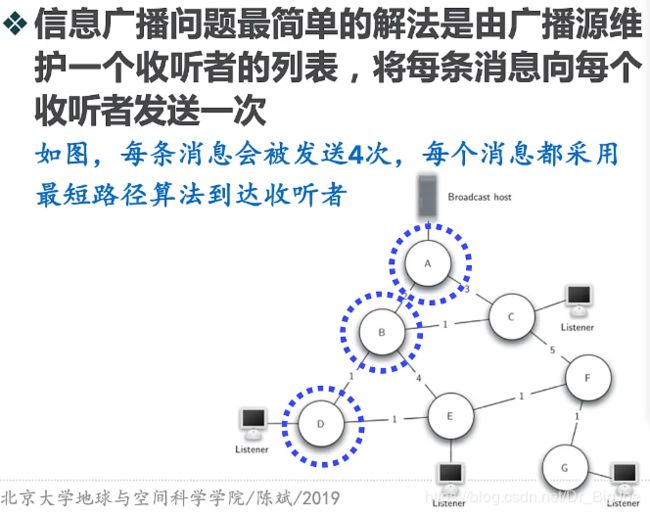
信息广播问题：单播解法

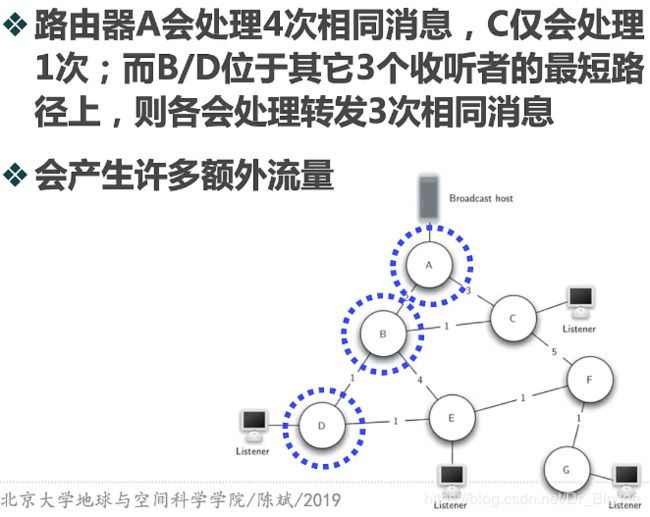
信息广播问题：洪水解法

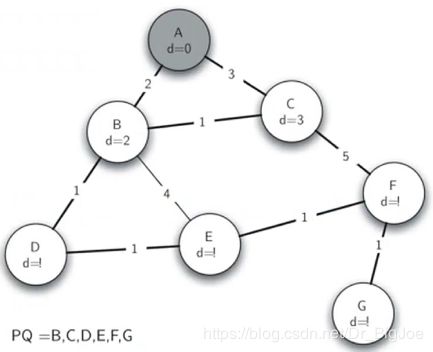
信息广播问题：最小生成树

• 信息广播问题的最优解法，依赖于路由器关系图上选取的具有最小权重的生成树(minimum weight spanning tree)。生成树：拥有图中所有的顶点和最少数量的边，以保持连通的子图。

• 图G(V,E)的最小生成树T，定义为：包含所有顶点V，以及E的无圈子集，并且边权重之和最小。

  

• 这样信息广播就只需要从A开始，沿着树的路径层次向下传播，就可以达到每个路由器只需要处理1次消息，同时总费用最小。

最小生成树：prim算法

• 解决最小生成树问题的Prim算法，属于贪心算法，即每步都沿着最小权重的边向前搜索。

• 构造最小生成树的思路很简单，如果T还不是生成树，则反复做：找到一条最小权重的可以安全添加的边，将边添加到树T。

• 可以安全添加的边，定义为一端顶点在树中，另一端不在树中的边，以便保持树的无圈特性。

  
  
  

最小生成树：prim算法代码实现

from pythonds.graphs import PriorityQueue,Graph,Vertex
import sys

def prim(G,start):
    pq = PriorityQueue()
    for v in G:
        v.setDistance(sys.maxsize)
        v.setPred(None)
    start.setDistance(0)
    pq.buildHeap([(v.getDistance(),v) for v in G])
    while not pq.isEmpty():
        currentVert = pq.delMin()
        for nextVert in currentVert.getConnections():
            newCost = currentVert.getWeight(nextVert)
            # nextVert在pq优先队列里，就不在生成树里，说明是可以安全添加的边
            if nextVert in pq and newCost < nextVert.getDistance():
                nextVert.setPred(currentVert)
                nextVert.setDistance(newCost)
                pq.decreaseKey(nextVert,newCost)

==================================================================
以上均为个人学习笔记总结，学习代码见week18
课程名称：数据结构与算法Python版_北京大学_中国大学MOOC(慕课)
课程主页: http://gis4g.pku.edu.cn/course/pythonds/