LSGAN

《Least Squares Generative Adversarial Networks》

github

Goodfellow在2014年发表了《Generative Adversarial Nets》后，生成对抗网络就引起深度学习领域的关注。它通过一种双人博弈的过程，迭代的优化生成器和判别器，最终到达纳什均衡点。

在标准的GAN中，判别器$D$的损失函数使用的是交叉熵，虽然最后可以生成效果不错的图像，但是GAN会存在以下两个问题：

• 梯度消失
• 模式坍缩

为了解决这两个问题，作者提出了LSGAN，$D$的损失函数改为使用最小二乘损失，通过实验证明了这种改变不仅可以生成更高质量的图像，而且训练过程更加的稳定，可以有效地解决模式坍缩问题。下面我们就看一下LSGAN是如何解决这两个问题的。

---

梯度消失问题的出现以及LSGAN的解决方案

在传统的GAN中使用的是交叉熵损失，由它定义的目标函数为：
$$\underset{G}{\min }\underset{D}{\max }V(G,D)=E_{x\sim p_{data}(x)}logD(x_i)+E_{x\sim p_z(z)}log(1-D(G(z_i)))$$
虽然GoodFellow在文中提出，可以使用最大化$\log D(G(z))$来代替最小化$\log (1-D(G(z)))$来避免梯度消失问题的过早出现，但是仍然无法从根本上解决这个问题。

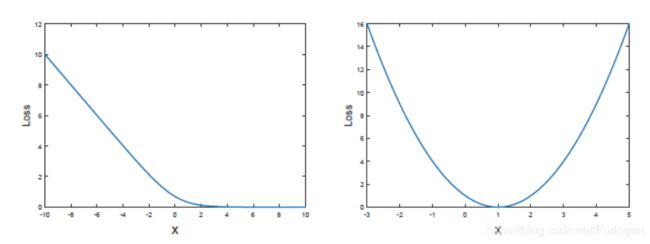
根源在于损失函数的选择，其他的方法只能使得梯度消失晚一点出现，而不是解决这个问题。从交叉熵损失函数的图来看，如下所示，随着$x$的增大，Loss会很快降为零，此时梯度达到饱和状态，$D$无法再给$G$提供梯度信息来使$G$进一步的更新，这样的话整个迭代过程就会停滞，整个模型的效果就不会很好。

而在LSGAN中使用的最小二乘损失的函数图如下右图所示，它也存在Loss为零的点，但是随着$x$的增大，它会很快地逃离梯度饱和的位置，从而从根源上解决了梯度消失这个问题。

从另一个角度来看，我们同样可以看出最小二乘损失是如何解决这个问题的。在交叉熵中使用的是Sigmoid函数，它可以使得$D$判别出输入样本是来自真实数据分布还是生成器，但是Sigmoid函数会很快的饱和。类似于它的LR中的使用，LR只关注数据是否正确的落在了决策边界的一边，而不关注数据距离决策边界的远近，这意味着Sigmoid函数不会惩罚距离边界较远的数据点。换言之，只要它成功的欺骗了$D$，就不会再为$G$提供更新的梯度信息，所以会很快的出现梯度消失。

而在最小二乘损失中，它使得$D$不仅需要正确的判别样本的来源，还会惩罚那些即使分类正确但距离决策边界较远的数据点，将其拉到距离边界较近的地方。在这个过程中，这些数据点会持续的为$G$提供梯度信息，从而一定程度上很好的解决了梯度消失的问题，而且训练的过程也更加稳定。

---

生成图像质量不高问题的出现以及LSGAN的解决方案

在传统的使用交叉熵损失的GAN中，它的决策边界如下图中蓝色所示，只要数据点被正确分类即可。但是有很多的数据点虽然被正确分类，但是它们距离决策边界很远，也就是说它所满足的分布和真实数据分布之间差异很大，导致了生成的图像很难逼近真实的图像。

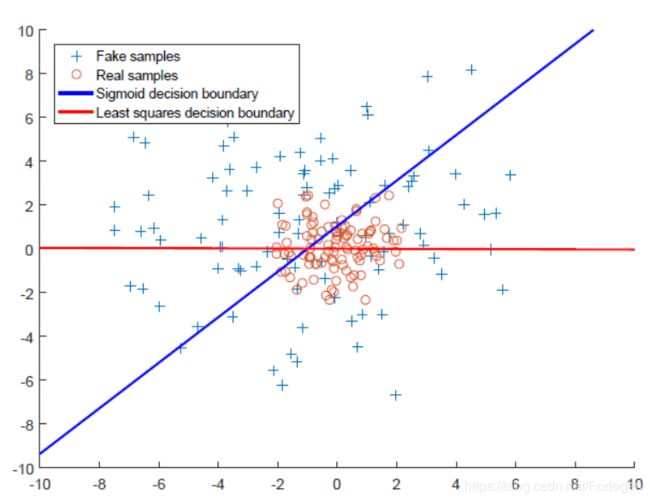
而在LSGAN中使用的最小二乘损失会将正确分类但距离决策边界较远的点拉近，使得整体的数据点距离边界先相比于前面近得多，即处理后它们所满足的分布更加接近真实数据分布，从而很好的提高了生成图像的质量。

---

理论分析

结合标准的GAN的目标函数和上面的分析，LSGAN的整体的训练过程可以表示为如下的形式：
$$\begin{array}{rl}\underset{D}{\min }{V}_{\mathrm{L}\mathrm{S}\mathrm{G}\mathrm{A}\mathrm{N}}(D)& =\frac{1}{2}{\mathbb{E}}_{\mathbf{x}\sim p_{\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}}(\mathbf{x})}\left[(D(\mathbf{x})-b{)}^2\right]+\frac{1}{2}{\mathbb{E}}_{\mathbf{z}\sim p_{\mathbf{z}}(\mathbf{z})}\left[(D(G(\mathbf{z}))-a{)}^2\right]\\ \underset{G}{\min }{V}_{\mathrm{L}\mathrm{S}\mathrm{G}\mathrm{A}\mathrm{N}}(G)& =\frac{1}{2}{\mathbb{E}}_{\mathbf{z}\sim p_{\mathbf{z}}(\mathbf{z})}\left[(D(G(\mathbf{z}))-c{)}^2\right]\end{array}$$
其中$G$代表生成器，$D$代表判别器，$z$代表输入的噪声向量，满足$z\sim p_z$，$p_{data}$代表真实数据的分布。

确定其中$a、b、c$值的一种方法是:使其满足$b-c=1$和$b-a=2$ ，目标函数最小化的过程，就是最小化$p_d+p_g$和$2p_g$之间$Pearson{\chi }^2$ 散度的过程。

• 当$a=-1,b=1,c=0$，得到如下目标函数:
  $$\begin{array}{rl}\underset{D}{\min }{V}_{\mathrm{L}\mathrm{S}\mathrm{G}\mathrm{A}\mathrm{N}}(D)& =\frac{1}{2}{\mathbb{E}}_{\mathbf{x}\sim p_{\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}}(\mathbf{x})}\left[(D(\mathbf{x})-1{)}^2\right]+\frac{1}{2}{\mathbb{E}}_{\mathbf{z}\sim p_{\mathbf{z}}}\left[(D(G(\mathbf{z}))+1{)}^2\right]\\ \underset{G}{\min }{V}_{\mathrm{L}\mathrm{S}\mathrm{G}\mathrm{A}\mathrm{N}}(G)& =\frac{1}{2}{\mathbb{E}}_{\mathbf{z}\sim p_{\mathbf{z}}(\mathbf{z})}\left[(D(G(\mathbf{z})){)}^2\right]\end{array}$$

• 当$b=c$ 时，例如使用0-1标签，可以得到如下的目标函数：
  $$\begin{array}{rl}\underset{D}{\min }{V}_{\mathrm{L}\mathrm{S}\mathrm{G}\mathrm{A}\mathrm{N}}(D)& =\frac{1}{2}{\mathbb{E}}_{\mathbf{x}\sim p_{\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}}(\mathbf{x})}\left[(D(\mathbf{x})-1{)}^2\right]+\frac{1}{2}{\mathbb{E}}_{\mathbf{z}\sim p_{\mathbf{z}}}\left[(D(G(\mathbf{z}))+1{)}^2\right]\\ \underset{G}{\min }{V}_{\mathrm{L}\mathrm{S}\mathrm{G}\mathrm{A}\mathrm{N}}(G)& =\frac{1}{2}{\mathbb{E}}_{\mathbf{z}\sim p_{\mathbf{z}}(\mathbf{z})}\left[(D(G(\mathbf{z})){)}^2\right]\end{array}$$

对上式求导得到$D$的最优解$D^{\ast }$:
$$D^{\ast }(\mathbf{x})=\frac{b{p}_{\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}}(\mathbf{x})+a{p}_g(\mathbf{x})}{p_{\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}}(\mathbf{x})+p_g(\mathbf{x})}$$
将其代入${\min }_G{V}_{\mathrm{L}\mathrm{S}\mathrm{G}\mathrm{A}\mathrm{N}}(G)=\frac{1}{2}{\mathbb{E}}_{\mathbf{x}\sim p_{\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}}(\mathbf{x})}\left[(D(\mathbf{x})-c{)}^2\right]+\frac{1}{2}{\mathbb{E}}_{\mathbf{z}\sim p_{\mathbf{z}}(\mathbf{z})}\left[(D(G(\mathbf{z}))-c{)}^2\right]$ 后，设$b-c=1,b-a=2$ 有：
$$\begin{array}{rl}2C(G)& ={\int }_{\mathcal{X}}\frac{{\left(2p_g(\mathbf{x})-\left(p_{\mathrm{d}}(\mathbf{x})+p_g(\mathbf{x})\right)\right)}^2}{p_{\mathrm{d}}(\mathbf{x})+p_g(\mathbf{x})}\mathrm{d}x\\ & ={\chi }_{\text{ Pearson }}^2\left(p_{\mathrm{d}}+p_g\Vert 2p_g\right)\end{array}所以说$$
所以说目标函数最小化的过程，就是最小化$p_d+p_g$和$2p_g$之间$Pearson{\chi }^2$ 散度的过程。

---

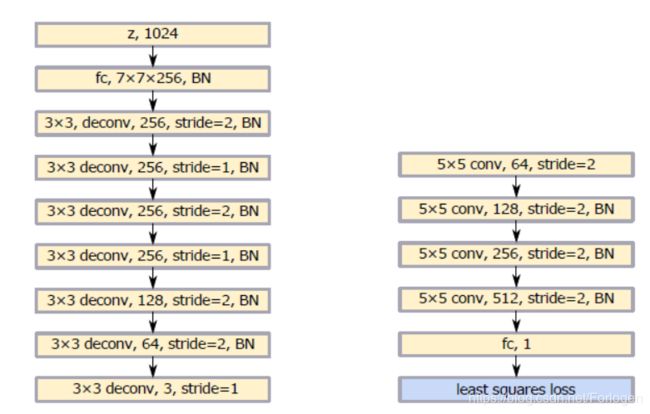
模型架构

• 当待处理的数据中类别较少时，$G$和$D$的网络架构如下所示：

  
  

• 当待处理的数据中类别较多时，$G$和$D$的网络架构如下所示：

  
  

---

实验

作者在多个数据集上进行实验，比较LSGAN和传统的GAN的稳定性。其中在 LSUN （ 使用了里面的 bedroom, kitchen, church, dining room 和 conference room 五个场景）和 HWDB1.0 的这两个数据集上使用 LSGANs 的效果如下所示：

其中在Bedroom中还对比了DCGAN和EBGAN和LSGAN的效果，从中我们可以看出，LSGAN的效果由于其他两个。

此外通过和传统的GAN比较，也可以看出LSGAN的效果要好很多

在显示LSGAN解决模式坍缩问题上，作者使用 LSGANs 和 GANs 学习混合高斯分布的数据集，如下所示：

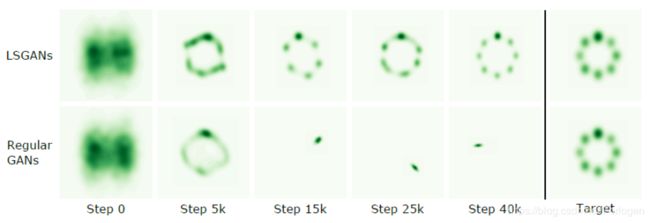
从中可以看出，传统 GAN 在 Step 15k 时就会发生模式坍缩现象，但 LSGANs 非常成功地学习到了混合高斯分布。

在实验的过程中，作者提出了如下的几个训练技巧：

• G 带有 batch normalization 批处理标准化（以下简称 BN）并且使用 Adam 优化器的话，LSGANs 生成的图片质量好，但是传统 GANs 从来没有成功学习到，会出现 mode collapse 现象；

• G 和D 都带有 BN 层，并且使用 RMSProp 优化器处理，LSGANs 会生成质量比 GANs 高的图片，并且 GANs 会出现轻微的 mode collapse 现象；

• G 带有 BN 层并且使用 RMSProp 优化器， G 、 D 都带有 BN 层并且使用 Adam 优化器时，LSGANs 与传统 GANs 有着相似的表现；

• RMSProp 的表现比 Adam 要稳定，因为传统 GANs 在 G 带有 BN 层时，使用 RMSProp 优化可以成功学习，但是使用 Adam 优化却不行

---

---

参考

https://blog.csdn.net/pandamax/article/details/61918899

https://blog.csdn.net/c9Yv2cf9I06K2A9E/article/details/83005495

https://blog.csdn.net/Hansry/article/details/83862548

https://www.jiqizhixin.com/articles/2018-10-10-11

https://zhuanlan.zhihu.com/p/25768099

https://www.cnblogs.com/shouhuxianjian/p/8467845.html

https://cloud.tencent.com/developer/news/325306

https://blog.csdn.net/victoriaw/article/details/60755698