推荐系统矩阵分解-基于SVD协同过滤的推荐

奇异值分解（Singular value decomposition）是一种矩阵分解技术，也是一种提取信息的方法。将一个比较复杂的矩阵用更小更简单的3个子矩阵的相乘来表示，这3个小矩阵描述了大矩阵重要的特性，可以起到降维简化数据，去除数据噪声的作用。通常，我们熟知的应用是将 SVD 应用到 PCA 降维中。
关于SVD，请见奇异值分解SVD，里面还有链接-PCA和SVD的区别和联系。

• SVD在推荐系统中到底在什么位置呢？
  推荐系统 -> 协同过滤算法 -> 隐语义模型 -> 矩阵分解 -> SVD

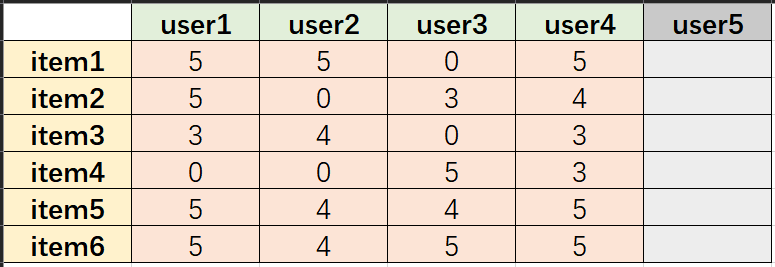
SVD就是用来将一个大的矩阵以降低维数的方式进行有损地压缩。假设我们有一个矩阵，该矩阵每一列代表一个user，每一行代表一个item。

矩阵值代表评分（0代表未评分），user5暂不计入该矩阵，将上述矩阵命名为 $A$：

A =

     5     5     0     5
     5     0     3     4
     3     4     0     3
     0     0     5     3
     5     4     4     5
     5     4     5     5

，则将矩阵 $A$ 作SVD，有：

[U,S,Vtranspose]=svd(A)

U =
   -0.4472   -0.5373   -0.0064   -0.5037   -0.3857   -0.3298
   -0.3586    0.2461    0.8622   -0.1458    0.0780    0.2002
   -0.2925   -0.4033   -0.2275   -0.1038    0.4360    0.7065
   -0.2078    0.6700   -0.3951   -0.5888    0.0260    0.0667
   -0.5099    0.0597   -0.1097    0.2869    0.5946   -0.5371
   -0.5316    0.1887   -0.1914    0.5341   -0.5485    0.2429
   
S =
   17.7139         0         0         0
         0    6.3917         0         0
         0         0    3.0980         0
         0         0         0    1.3290
         0         0         0         0
         0         0         0         0
         
Vtranspose =
   -0.5710   -0.2228    0.6749    0.4109
   -0.4275   -0.5172   -0.6929    0.2637
   -0.3846    0.8246   -0.2532    0.3286
   -0.5859    0.0532    0.0140   -0.8085

其中，$S$ 很特殊，是个对角线矩阵，每个元素非负，而且依次减小，表示奇异值（可以理解为EVD中的特征值，后直接称为特征值）。可以大致理解为：在线性空间里，每个向量代表一个方向，所以特征值是代表该矩阵向着该特征值对应的特征向量的方向的变化权重。

取 $S$ 对角线上前 $k$ 个元素。当 $k=2$ 时候即将 $S(6\times 4)$ 降维成 $S(2\times 2)$，同时 $U(6\times 6),Vtranspose(4\times 4)$ 相应地变为 $U(6\times 2),Vtranspose(4\times 2)$. 可得到如下图：

其中，$U$ 可以看作是 item 的某种潜在因子（隐向量表示），V看作 user 的某种潜在因子（隐向量表示），此时我们用降维后的 $U,S,V$ 来相乘得到 $A2$，有：

A2=U(1:6,1:2)*S(1:2,1:2)*(V(1:4,1:2))'
A2 =

    5.2885    5.1627    0.2149    4.4591
    3.2768    1.9021    3.7400    3.8058
    3.5324    3.5479   -0.1332    2.8984
    1.1475   -0.6417    4.9472    2.3846
    5.0727    3.6640    3.7887    5.3130
    5.1086    3.4019    4.6166    5.5822

可以看出，$A2$ 和 $A$ 很接近，所以，基于SVD的降维（PCA）还可以看作是数据的有损压缩。

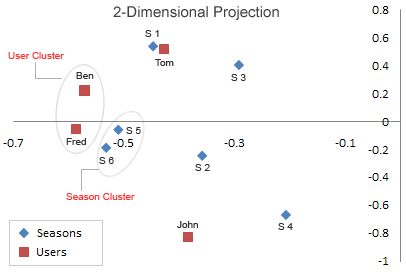
将 $U$ 的第一列当成 $x$ 值，第二列当成 $y$ 值，user1-4 对应 Ben | Tom | John | Fred，即 $U$ 的每一行用一个二维向量表示，同理 $V$ 的每一行也用一个二维向量表示，item1-6 对应Season 1 Season 2 Season 3 Season 4 Season 5 Season 6，有：

从图中可以看出，Season5，Season6特别靠近。Ben 和 Fred 也特别靠近。同时我们仔细看一下 $A$ ，可以发现，$A$ 的第 5 行向量和第 6 行向量特别相似，Ben 所在的列向量和 Fred 所在的列向量也特别相似。

假设，现在有个名字叫Bob的新用户（其实，在现在的推荐系统中，会把这个用户放到矩阵 $A$ 中参与计算，那样可以直接补全评分矩阵，从而直接进行推荐），并且已知这个用户对season n的评分向量为：$[5,5,0,0,0,5{]}^T$。（此向量为列向量）。现在任务是要对他做出个性化的推荐，首先是利用新用户的评分向量找出该用户的相似用户。
$Bo{b}_{2D}=Bo{b}^T\times U_2\times S_k^{-1}$
其中，$Bo{b}^T=[5,5,0,0,0,5]$，上式：

Bob_{2D}=
[5,5,0,0,0,5]   
X
 [[-0.4472   -0.5373]   
 [-0.3586    0.2461]   
 [-0.2925   -0.4033]   
 [-0.2078    0.6700]   
 [-0.5099    0.0597]  
 [-0.5316    0.1887]]   
X 
[[17.7139         0]    
       [0    6.3917]]


=[0.3775 0.0802]

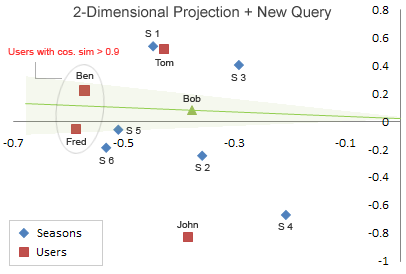
得到一个Bob的二维向量（隐向量表示），即知道Bob的坐标。将Bob坐标添加进原来的图中：

从图中用余弦相似度计算找出和Bob最相似的用户（基于user的协同过滤推荐，为什么要进行SVD呢？哈哈哈，这个例子不太好，但可以顺便回顾一下基于user的协同过滤推荐），计算出最相似的用户是ben。观察ben的评分向量为：【5 5 3 0 5 5】，对比Bob的评分向量：【5 5 0 0 0 5】。然后找出ben评分过而Bob未评分的 item 并排序，即【season 5：5，season 3：3】，即推荐给Bob的item依次为 season5 和 season3。

总结：

• SVD本身就是时间复杂度高的计算过程，如果数据量大的情况恐怕时间消耗无法忍受。 不过可以使用梯度下降等机器学习的相关方法来进行近似计算，以减少时间消耗。 paper [A Guide to Singular Value Decomposition for Collaborative Filtering] 中总结了几种SVD的方法，它们都是用梯度下降来进行求解的。
• 相似度计算方法的选择，有多种相似度计算方法，每种都有对应优缺点，对针对不同场景使用最适合的相似度计算方法。在推荐系统中，最常用的相似度计算方法是余弦相似度。
• 推荐策略：首先是相似用户可以多个，每个由相似度作为权重来共同影响推荐的 item 的评分。

推荐阅读：
从SVD到推荐系统
SVD在推荐系统中的应用