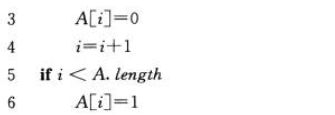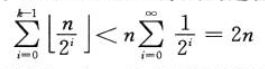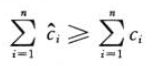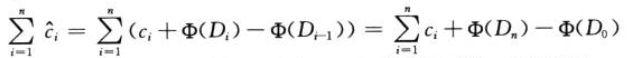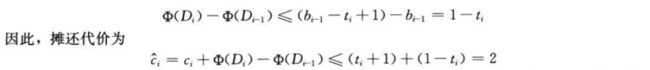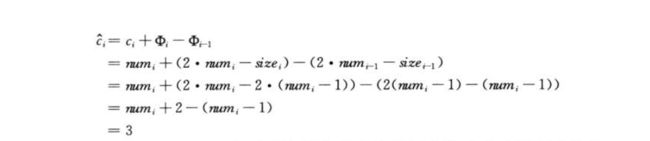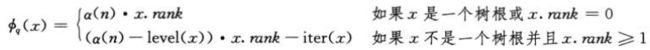0.目录
- 1.聚合分析
1.1 聚合分析的核心要点
1.2 聚合分析的实例
1.2.1 栈操作
1.2.2 二进制计数器递增
1.2.3 动态表 - 2.核算法
2.1 核算法的核心要点(信用与特定对象相关联)
2.2 核算法的实例
2.2.1 栈操作
2.2.2 二进制计数器递增
2.2.3 动态表
2.2.4 二项队列的插入分析 - 3.势能法
3.1 势能法的核心要点(势能与整个数据结构相关联,而不是特定对象)
3.2 势能法的实例
3.2.1 栈操作
3.2.2 二进制计数器递增
3.2.3 动态表
3.2.4 二项队列的插入分析
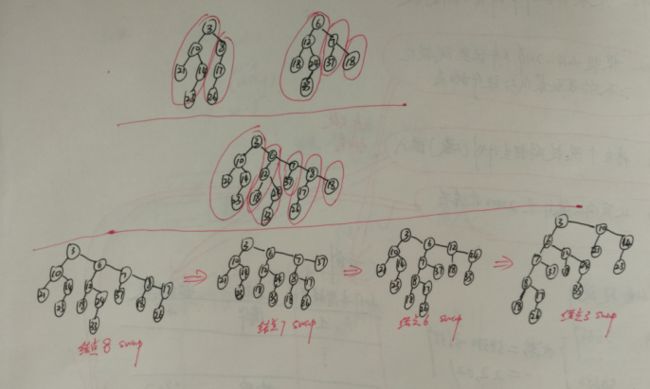
3.2.5 斜堆
3.2.6 斐波那契堆
3.2.7 伸展树
3.2.8 不相交集合——并查集
在摊还分析中,求数据结构的一个操作序列中所执行的所有操作的平均时间,来评价操作的代价。
摊还分析不同于评价情况分析,它并不涉及概率。
摊还分析最常用的三种技术:
- 聚合分析:这种方法用来确定一个n个操作序列的总代价的上界T(n),因此每个操作的平均代价为T(n)/n
- 核算法:用来分析每个操作的摊还代价。核算法将序列中某些较早的操作的“余额”作为“预付信用”存储起来,与数据结构中的特定对象相关联。在操作序列中随后的部分,存储的信用即可用来为拿些缴费少于实际代价的操作支付差额
- 势能法:也是分析每个操作的摊还代价,也是通过较早的操作的余额来补偿稍后操作的差额。势能法将信用作为数据结构的势能存储起来,且将势能作为一个整体存储,而不是将信用与数据结构中单个对象关联分开存储。
1.聚合分析
1.1 聚合分析的核心要点
利用聚合分析,我们证明对所有n,一个n个操作的序列最坏情况下花费的总时间为T(n)。因此,在最坏情况下,每个操作的平均代价,或摊还代价为T(n)/n。
此摊还代价是适用于每个操作的,即使序列中有多种类型的操作也是如此。
1.2 聚合分析的实例
1.2.1 栈操作
基本的栈操作,时间复杂性均为O(1):
- PUSH(S, x):将对象x压入栈S中
- POP(S):将栈S的栈顶对象弹出,并返回该对象。对空栈调用POP产生错误
新增一个栈操作MULTIPOP(S, k):删除栈S栈顶的k个对象,如果栈中对象数少于k,则将整个栈的内容都弹出。
一个包含s个对象展现执行MULTIPOP(S, k),总代价为min(s, k)。
聚合分析:
考虑整个序列的n个操作,在一个空栈上执行n个PUSH、POP和MULTIPOP的操作序列,代价至多O(n)。
因为将一个对象压入栈后,至多将其弹出一次,对一个非空的栈,可以执行的POP操作的次数(包括MULTIPOP中调用POP次数)最多与PUSH操作的次数相当,即最多n次。因此,对任意的n值,任意一个有n个PUSH、POP和MULTIPOP的操作序列,最多花费O(n)时间。
因此三种栈操作的摊还代价为O(1)。
1.2.2 二进制计数器递增
k位二进制计数器递增的问题,计数器的初值为0.
用一个位数组A[0..k-1]作为计数器,其中A.length = k。当计数器中保存的二进制值为x时,x的最低位保存在A[0],而最高位保存在A[k-1]中。因此:
最坏情况:INCREMENT执行一次花费Θ(k)时间。
聚合分析:
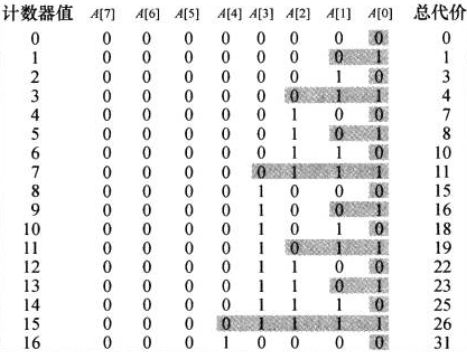
每次调用INCREMENT是A[0]确实都会翻转;
A[1]每两次调用翻转一次;
A[2]每四次调用才翻转一次;
...
因此,对于一个初值为0的计数器,在执行一个由n个INCREMENT操作组成的序列的过程中,进行翻转的总数为:
因此,对一个初值为0的计数器,执行一个n个INCREMENT操作的序列的最坏情况时间为O(n)。每个操作的平均代价,即摊还代价为O(1)。
1.2.3 动态表
对某些应用程序,无法预知将会有多少个对象存储在表中。
不够用时,必须为其分配更大的空间,并将所有对象从原表中复制到新的空间中;
若从表中删除了很多对象,为其重新分配一个更小的内存空间就是值得的。
使用摊还分析证明,虽然插入和删除操作可能会引起扩张或收缩,从而有较高的实际代价,但它们的摊还代价都是O(1),并保证动态表中的空闲空间相对于总空间的比例永远不超过一个常量分数。
装载因子α:表中存储的数据项数量 除以 表的规模(槽的数量)。
1)表扩张——只允许插入数据项
一个常用的分配新表的启发式策略:为新表分配2倍于旧表的槽。如果只允许插入操作,那么装载因子总是保持在1/2以上,因此,浪费的空间永远不会超过总空间的一半。
如下,T对应表:
T.table保存指向表的存储空间的指针;
T.num保存表中的数据项数量
T.size保存表的规模(槽数)
运行时间分析:
将每次基本插入操作的代价设定为1,然后用基本插入操作的次数来描述TABLE-INSERT的运行时间。
最坏情况分析:
第i个操作的代价ci。如果当前表满,会发生一次扩张,则ci = i:基本插入操作代价1,加上从旧表到新表的复制代价i-1。
聚合分析:
执行n个TABLE-INSERT操作,扩张动作是很少的,仅当i-1恰为2的幂时,第i个操作才会引起一次扩张。
因此单一操作的摊还代价至多为3
2)表扩张和收缩——既允许插入也允许删除
见势能法
2.核算法
2.1 核算法的核心要点(信用与特定对象相关联)
- 用核算法进行摊还分析,对不同操作赋予不同费用,赋予某些操作的费用可能多于或少于其实际代价。将赋予一个操作的费用称为它的摊还代价。
- 信用:当一个操作的摊还代价超出其实际代价时,将差额存入数据结构中的特定对象,存入的差额称为信用。
对于后续操作中摊还代价小于实际代价的情况,信用可以用来支付差额。因此,将一个操作的摊还代价分解为其实际代价和信用(存入的或用掉的)
不同的操作可能有不同的摊还代价,不同于聚合分析。 -
必须小心地选择操作的摊还代价。若希望通过分析摊还代价来证明每个操作的平均代价的最坏情况很小,就应确保操作序列的总摊还代价给出了序列总真实代价的上界。这种关系必须对所有操作序列都成立。
左边为总摊还代价,右边总实际代价。
数据结构中存储的信用为两者的差值,信用必须一直为非负值。
2.2 核算法的实例
2.2.1 栈操作
1)操作的实际代价为:
2)为这些操作赋予如下摊还代价:
为什么这样赋值(特点——信用与特定的对象绑定在一起,例如这里每个元素都绑定一个预存的信用):
为每个入栈的元素存储对应的一个信用(一个实际代价+一个信用=总数为2),作为POP和MULTIPOP弹出时使用。因此,对任意n个PUSH、POP、MULTIPOP操作组成的序列,总摊还代价为总实际代价的上界。
由于总摊还代价为O(n),因此总实际代价也是。
2.2.2 二进制计数器递增
1)操作的实际代价
置位 1
复位 1
2)为这些操作赋予如下摊还代价:
置位 2
复位 0
为什么这样赋值:
进行置位时,用1支付置位操作的实际代价,并将另外1存为信用,用来支付将来复位操作的代价。
在任何时候,计数器中任何为1的位都存有1的信用,这样对于复位操作,就无需缴纳任何费用。
INCREMENT的摊还代价:
INCREMENT过程至多置位一次,因此,其摊还代价最多为2.
计数器中1的个数永远不会为负,因此,任何时刻信用都是非负。因此,对于n个INCREMENT操作,总摊还代价为O(n),为总实际代价的上界。
2.2.3 动态表
装载因子α:表中存储的数据项数量 除以 表的规模(槽的数量)。
1)表扩张——只允许插入数据项
为每次插入赋予摊还代价为3,为什么赋值为3:
假定表的规模在一次扩张后边为m,则表中保存了m/2个数据项,且它没有存储任何信用。为每次插入操作付3的代价,3的分配如下:
2)表扩张和收缩——既允许插入也允许删除
见势能法
2.2.4 二项队列的插入分析
类似于二进制计数器
为这些操作赋予如下摊还代价:
插入 2
链接 0
为什么这样赋值:
进行插入时,用1支付置位操作的实际代价,并将另外1存为信用,用来支付将来该位置上链接操作的代价。
在任何时候,二项队列中任何有树的位都存有1的信用,这样对于链接操作,就无需缴纳任何费用。
插入的摊还代价:
插入过程至多置位一次,因此,其摊还代价最多为2.
二项队列中树的个数永远不会为负,因此,任何时刻信用都是非负。因此,对于n个插入操作,总摊还代价为O(n),为总实际代价的上界。
3.势能法
3.1 势能法的核心要点(势能与整个数据结构相关联,而不是特定对象)
- 势能法摊还分析将预付代价表示为势能,将势能释放即可用来支付未来操作的代价。将势能与整个数据结构而不是特定对象相关联
-
势能法工作方式
每个操作的摊还代价等于其实际代价加上此操作引起的势能变换。n个操作总的摊还代价为:
证明很简单,另Φ'(Di) = Φ(Di) - Φ(D0) 即可。
3.2 势能法的实例
3.2.1 栈操作
step1. 势函数的定义
定义为栈中的对象数量。对于初始的空栈Φ(D0) =0.
由于栈中对象数据永远不可能为负,因此,第i步操作得到的栈Di具有非负的势:
因此,用Φ定义的n个操作的总摊还代价即为实际代价的一个上界。
step2. 计算不同栈操作的摊还代价
step3. 计算n个操作的总摊还代价
每个操作的摊还代价都是O(1),因此,n个操作的总摊还代价为O(n)。由于Φ(Di) >= Φ(D0) ,因此,n个操作的总摊还代价为总实际代价的上界。所以n个操作的最坏情况时间为O(n)。
3.2.2 二进制计数器递增
step1. 势函数的定义
bi——i次操作后计数器中的1的个数
Φ(D0) = 0,由于计数器中1的个数为非负数,因此Φ(Di) >= 0.
step2. 计算不同操作的摊还代价——INCREMENT操作
step3. 计算n个操作的总摊还代价
Φ(D0) = 0,由于计数器中1的个数为非负数,因此Φ(Di) >= 0.
所以,一个n个INCREMENT操作序列的总摊还代价是总实际代价的上界,所以n个INCREMENT操作的最坏情况时间O(n)。
计时器不是0开始也可以分析:
3.2.3 动态表
装载因子α:表中存储的数据项数量 除以 表的规模(槽的数量)。
1)表扩张——只允许插入数据项
step1. 势函数的定义
定义势函数Φ,在扩张后其值为0,表满时其值为表的规模,这样就可以用势能来支付下次扩张的代价。
势能的初值为0,且表总是至少半满的,即T.num >= T.size/2,于是Φ(T)总是非负的。因此,n个TABLE-INSERT操作的摊还代价之和给出了实际代价之和的上界。
step2. 计算操作的摊还代价
step3. 计算n个操作的总摊还代价
因此,n个操作的总摊还代价为O(n)。
2)表扩张和收缩——既允许插入也允许删除
为了限制浪费的空间,可以在装载因子变得太小时对表进行收缩操作。
希望保持两个性质:
- 动态表的装载因子有一个正的常数下界
- 一个表操作的摊还代价有一个常数上界
一个错误的策略:
当插入一个数据项到满表时将表的规模加倍,当删除一个数据项导致表空间利用率不到一半时就应该将表的规模减半。
考虑一种场景:插入一个满表时,,扩张(一半);删除两个,不到一半,收缩;插入两个,满表.....这样反复的两次插入、两次删除会导致代价为Θ(n)
改进策略:
允许装载因子低于1/2,设置为1/4.
当插入一个满表时,仍然将表规模加倍,但只有当装载因子小于1/4而不是1/2时,才将表规模减半。
step1. 势函数的定义
1)当装载因子为1/2,表的势能为0
2)随着装载因子偏离1/2,势能应该增长,使得当扩张或收缩表时,表已经存储了足够的势能来支付复制所有数据项至新表的代价
3)因此,当装载因子为1或下降为1/4时,势函数增长为T.num
step2. 计算不同操作的摊还代价
1)插入操作
2)删除操作
step3. 计算n个操作的总摊还代价
由于每个操作的摊还代价的上界是一个常数,在一个动态表上执行任意n个操作的实际运行时间是O(n)
3.2.4 二项队列
类似于二进制计数器
step1. 势函数的定义
定义为第i次插入后树的棵树。
step2. 计算不同操作的摊还代价
1)插入
2)合并和DeleteMin
DeleteMin本质上就是合并。
摊还代价 = 实际操作代价 + 势的增加(最多增加O(lgN))
另一种解释(不太合理,应该从程序出发,并利用摊还分析公式):而合并相当于在多个位上进行插入(可以视为连续的一系列插入),而在任何位上的插入都是等价的,摊还代价为2,所以最多有lgN个位(N = N1 + N2)。因此摊还代价为lgN。
step3. 计算n个操作的总摊还代价
3.2.5 斜堆
合并两个斜堆:
step1.把它们的右路径合并并使之成为新的左路径
step2.对于新路径上的每一个结点,出去最后一个外,老的左子树作为右子树而附于其上。
斜堆合并的的最坏情况是Θ(N):
1)上界显然是O(N)
2)找个特例,右路径长尾Θ(N)
step1. 势函数的定义
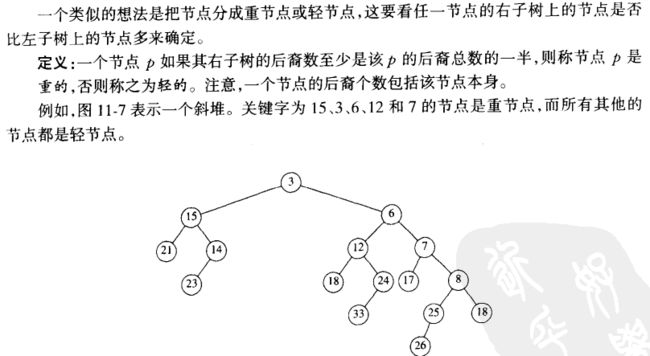
势函数定义为这些堆中的重结点个数。
为什么这么定义?
因为一条长的右路径将包括非常多的重结点,由于这条路径上的结点将要交换它们的子节点,因此这些结点将转变成合并结果中的轻结点。(势能有减小的趋势)
step2. 计算不同操作的摊还代价
step3. 计算n个操作的总摊还代价
3.2.6 斐波那契堆
参见http://www.jianshu.com/p/f62787325788
根节点(树的棵树)所形成的势正好用来支付链接操作(链接操作消耗代价)。
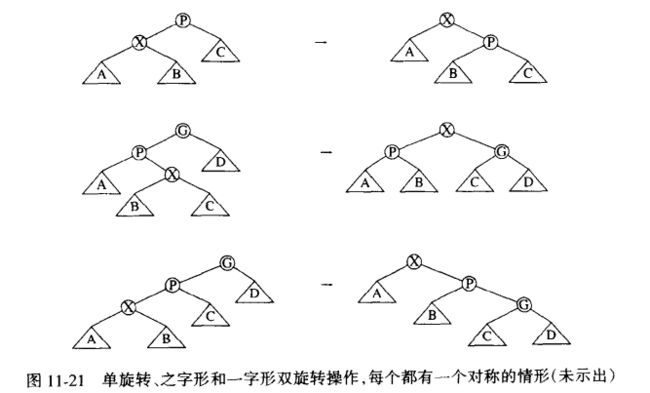
3.2.7 伸展树
3.2.8 不相交集合——并查集
关键思路:
- 秩的性质
- 函数Ak(n)及反函数α(n)
- 将Ak(n)及反函数α(n)作用于秩,并由此构造势函数,使得所有操作的摊还代价不超过O(α(n))
1)秩的性质
2)函数Ak(n)及反函数α(n)
3)势函数中level(x)及iter(x)性质——前提x.rank >=1
3-1) level(x)的性质——前提x.rank >=1
- level(x)是Ak的一个最大级k,其中Ak是作用于x的秩的函数,并且Ak不大于x的父节点的秩
- x.p.rank单调递增,则level(x)也单调递增
-
0 <= level(x) < α(n)
3-2) iter(x)的性质——前提x.rank >=1
- iter(x)是可以迭代地实施Alevel(x)的最大次数,开始时将Alevel(x)应用于x的秩,直至获得一个大于x的父节点的秩的值之前迭代停止
- 只要level(x)保持不变,iter(x)一定是增加或者保持不变的;
x.p.rank是单调递增的,为了使iter(x)能够减小,level(x)必须增加 -
1 <= iter(x) <= x.rank
4)证明中刚开始不理解的地方
4-1)定理21.13中,不满足限制的,路径上最后一个满足level(w) = k的结点,这里k = 0, 1, 2, ... ,α(n)-1.因为下一个结点,使得level(y)比level(x)大1,因此不满足
3.2.8-step1. 势函数的定义
定义q次操作后结点x的势:
其中的两个辅助函数定义如下:
证明势函数总是非负的,这样摊还代价的上界就是实际操作的上界:
3.2.8-step2. 计算不同操作的摊还代价
step2-1 MAKE-SET摊还代价
step2-2 LINK摊还代价
step2-3 FIND-SET摊还代价