数据结构-桶排序 计数排序 基数排序

注：所有的代码在我的 Github中有均具体C++代码实现。

这里主要讲的是三大线性排序：桶排序(Bucket sort)、计数排序(Counting sort)和基数排序(Radix sort)。

所谓线性排序，也就是说时间复杂度为 O(n)，而之所以能够做到线性排序，是因为这三个算法是非基于比较的排序算法，都不涉及元素之间的比较操作。

桶排序(Bucket sort)

简介

顾名思义，会用到“桶”，核心的思想就是将要排序的数据分到几个有序的桶里面，然后每个桶再进行单独的排序。桶内的数据排序过后，再把每个桶里面的数据依次取出，这样组成的序列就是有序的了。

时间复杂度

如果要排序的数据有 n 个，我们把它们均匀地划分到 m 个桶内，每个桶里就有 k=n/m 个元素。每个桶内部使用快速排序，时间复杂度为 O(k * logk)。m 个桶排序的时间复杂度就是 O(m * k * logk)，因为 k=n/m，所以整个桶排序的时间复杂度就是 O(n*log(n/m))。当桶的个数 m 接近数据个数 n 时，log(n/m) 就是一个非常小的常量，这个时候桶排序的时间复杂度接近 O(n)。

使用场景

桶排序既然如此优秀，那它是不是可以替代其他的排序算法呢？

答案是否定的，上述的图展示的仅仅是一个理想的状态下，其实桶排序对排序数据的要求是非常严格的。

• 需要排序的数据应该很容易就能化成m个桶，并且桶和桶之间有着天然的大小顺序，这样每个桶排完序之后，桶和桶之间就不再需要进行排序了。
• 每个桶之间的分布数据应该是比较均匀的。试想一下，划分之后，如果有些桶里面的数据非常多，而有些桶里面的数据非常少的话，那不就退化成为了O(nlogn)的排序算法了么？

所以，桶排序更加适用于在外部排序当中：外部排序也就是数据存储在外部磁盘，数据量比较大，而内存是有限的，无法将数据全部加载到内存中。

例如：比如说我们有 10GB 的订单数据，我们希望按订单金额（假设金额都是正整数）进行排序，但是我们的内存有限，只有几百 MB，没办法一次性把 10GB 的数据都加载到内存中。这个时候该怎么办呢？

答：我们可以先扫描一遍文件，看订单金额所处的数据范围。假设经过扫描之后我们得到，订单金额最小是 1 元，最大是 10 万元。我们将所有订单根据金额划分到 100 个桶里，第一个桶我们存储金额在 1 元到 1000 元之内的订单，第二桶存储金额在 1001 元到 2000 元之内的订单，以此类推。每一个桶对应一个文件，并且按照金额范围的大小顺序编号命名（00，01，02…99）。理想的情况下，如果订单金额在 1 到 10 万之间均匀分布，那订单会被均匀划分到 100 个文件中，每个小文件中存储大约 100MB 的订单数据，我们就可以将这 100 个小文件依次放到内存中，用快排来排序。等所有文件都排好序之后，我们只需要按照文件编号，从小到大依次读取每个小文件中的订单数据，并将其写入到一个文件中，那这个文件中存储的就是按照金额从小到大排序的订单数据了。
不过，你可能也发现了，订单按照金额在 1 元到 10 万元之间并不一定是均匀分布的 ，所以 10GB 订单数据是无法均匀地被划分到 100 个文件中的。有可能某个金额区间的数据特别多，划分之后对应的文件就会很大，没法一次性读入内存。这又该怎么办呢？针对这些划分之后还是比较大的文件，我们可以继续划分，比如，订单金额在 1 元到 1000 元之间的比较多，我们就将这个区间继续划分为 10 个小区间，1 元到 100 元，101 元到 200 元，201 元到 300 元…901 元到 1000 元。如果划分之后，101 元到 200 元之间的订单还是太多，无法一次性读入内存，那就继续再划分，直到所有的文件都能读入内存为止。

计数排序（Counting sort）

简介

它的优势在于在对一定范围内的整数排序时，它的复杂度为Ο(n+k)（其中k是整数的范围），快于任何比较排序算法，是一种空间换取时间的算法，我们可以将其理解为一种特殊的桶排序。

例子

假设有几个考生，分数在0-5之间，这几个考生的成绩放在数组 A[8] 中

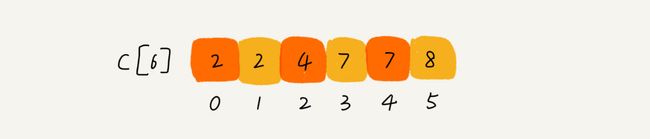
A[8] = {2, 5, 3, 0, 2, 3, 0, 3} 由于分数最高位 5， 最低为0， 所以我们使用一个长度为6的C[6]数组（计数数组）来记录每个分有多少名学生，依次为：

C[0] = 2 C[2] = 2 C[3] = 3 C[5] = 1

这样我们就能很快的计算出每个分数的考生在有序数组中对应的存储位置，我们可以得到一个新的C[6]数组，如下：

解释一下：

C[0]就代表得到 小于等于 0 分 的考生有2个；

C[1]就代表得到 小于等于 1分 的考生有2个；

C[2]就代表得到 小于等于 2 分 的考生有4个…

最终我们就知道了，原来小于等于5分的有8个人，那么我假如是5分，那么就正好排在第8 名(也救赎数组R中R[7]的位置)咯。

我们从后面往前扫描数组A：重新分配一个和A一样大小空间的数组R[8]

A[7] = 3 =>C[3] = 7=>R[7-1] = R[6] = 3===>C[3] –

A[6] = 0 =>C[0] = 2=>R[2-1] = R[1] = 0===>C[0] –

​ …

代码实现

void countSort(int *arr, int n)
{
    // 查找数组中的数据范围，即使是负数，同样也可以操作
	int max = getMax(arr, n);
	int min = getMin(arr, n);
	// 申请一个临时数组用来存储排序之后的数组
	int *sortedArr = new int[n + 1];
    // 申请一个计数数组
	int count[max - min + 1];
	// 计算每个元素出现的个数
	for (int i = 0; i < n; i++)
		count[arr[i] - min] ++;
	// 依次累加
	for (int i = 1; i < (max - min + 1); i++)
		count[i] += count[i - 1];
	// 关键部分，多看几遍
	for (int i = n - 1; i >= 0; i--)
	{
		sortedArr[count[arr[i] - min] - 1] = arr[i];
		count[arr[i] - min]--;
	}
    // 将结果拷贝回去给arr数组
	for(int i = 0; i < n; i++)
	{
		arr[i] = sortedArr[i]; 
	} 
	delete sortedArr;
}

总结

计数排序只能用在数据范围不大的场景中，如果数据范围k比要排序的数据n大得多，就不适合用计数排序了。

基数排序（Radix sort）

简介

基数排序是桶排序的扩展，它的基本思想是：将整数按位数切割成不同的数字，然后按每个位数分别比较。
具体做法是：将所有待比较数值统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。

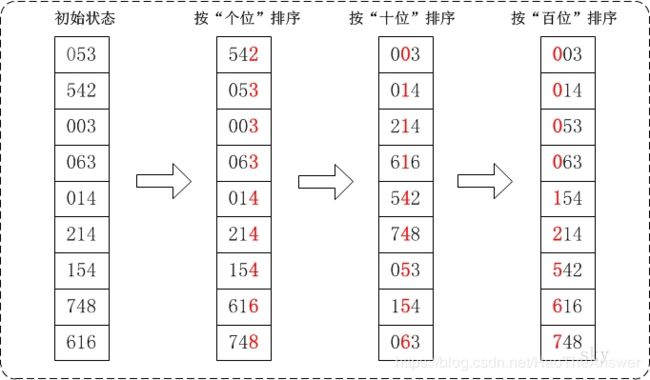
使用场景

假设我们有 10 万个手机号码，希望将这 10 万个手机号码从小到大排序，你有什么比较快速的排序方法呢？

这里，先按照最后一位来排序手机号码，然后，再按照倒数第二位重新排序，以此类推，最后按照第一位重新排序。经过 11 次排序之后，手机号码就都有序了。

所以请记住，基数排序算法是稳定的，不然这个思路就是不正确的了。因为如果是非稳定排序算法，那最后一次排序只会考虑最高位的大小顺序，完全不管其他位的大小关系，那么低位的排序就完全没有意义了。

实际上，有时候要排序的数据并不都是等长的，比如我们排序牛津字典中的 20 万个英文单词，最短的只有 1 个字母，最长的我特意去查了下，有 45 个字母，中文翻译是尘肺病。对于这种不等长的数据，基数排序还适用吗？实际上，我们可以把所有的单词补齐到相同长度，位数不够的可以在后面补“0”，因为根据ASCII 值，所有字母都大于“0”，所以补“0”不会影响到原有的大小顺序。这样就可以继续用基数排序了。

代码实现

void radixSort(int a[], int n)
{
	int output[n];
	int max = 0;
    // 找出最大数
	for (int i = 0; i < n; ++i)
	{
		if (a[i] > max)
		{
			max = a[i];
		}
	}
    // 计算最大数的位数
	int maxdigits = 0;
	while (max)
	{
		maxdigits ++;
		max /= 10;
	}
    // 逐位排序
	for (int j = 0; j < maxdigits; j++)
	{
		int k = 0;
		for (int p = 0; p < 10; p++) // 170, 45, 75, 90, 802, 24, 2, 66
		{
            // 针对第 j 位进行排序
			for (int i = 0; i < n; i++)
			{
				int t = pow(10, j);
				if ((a[i] % (10 * t)) / t == p)
					output[k ++] = a[i];
			}
		}
        // 第 j 位后的排序结果
		for (int i = 0; i < n; ++i)
		{
			a[i] = output[i];
		}
	}
}

总结

桶排序和计数排序的排序思想是非常相似的，都是针对范围不大的数据，将数据划分成不同的桶来实现排序。基数排序要求数据可以划分成高低位，位之间有递进关系。比较两个数，我们只需要比较高位，高位相同的再比较低位。而且每一位的数据范围不能太大，因为基数排序算法需要借助桶排序或者计数排序来完成每一个位的排序工作