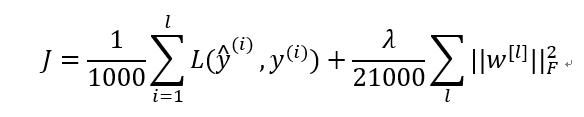吴恩达深度学习笔记(38)-优化算法(Optimization algorithms)

Mini-batch 梯度下降（Mini-batch gradient descent）
本周将学习优化算法，这能让你的神经网络运行得更快。

机器学习的应用是一个高度依赖经验的过程，伴随着大量迭代的过程，你需要训练诸多模型，才能找到合适的那一个，所以，优化算法能够帮助你快速训练模型。

其中一个难点在于，深度学习没有在大数据领域发挥最大的效果，我们可以利用一个巨大的数据集来训练神经网络，而在巨大的数据集基础上进行训练速度很慢。

因此，你会发现，使用快速的优化算法，使用好用的优化算法能够大大提高你和团队的效率，那么，我们首先来谈谈mini-batch梯度下降法。

你之前学过，向量化能够让你有效地对所有m个样本进行计算，允许你处理整个训练集，而无需某个明确的公式。

所以我们要把训练样本放大巨大的矩阵X当中去，X=[x^((1) ) x^((2) ) x^((3) )……x^((m) ) ]。

Y也是如此，Y=[y^((1) ) y^((2) ) y^((3) )……y^((m) ) ]。

所以X的维数是(n_x,m)，Y的维数是(1,m)，向量化能够让你相对较快地处理所有m个样本。如果m很大的话，处理速度仍然缓慢。比如说，如果m是500万或5000万或者更大的一个数，在对整个训练集执行梯度下降法时，你要做的是，你必须处理整个训练集，然后才能进行一步梯度下降法，然后你需要再重新处理500万个训练样本，才能进行下一步梯度下降法。所以如果你在处理完整个500万个样本的训练集之前，先让梯度下降法处理一部分，你的算法速度会更快，准确地说，这是你可以做的一些事情。

你可以把训练集分割为小一点的子集训练，这些子集被取名为mini-batch，假设每一个子集中只有1000个样本，那么把其中的x^((1))到x((1000))取出来，将其称为第一个子训练集，也叫做mini-batch，然后你再取出接下来的1000个样本，从x^((1001))到x((2000))，然后再取1000个样本，以此类推。

接下来我要说一个新的符号，把x^((1))到x((1000))称为X^({1})，x((1001))到x^{((2000))称为X}({2})，如果你的训练样本一共有500万个，每个mini-batch都有1000个样本，也就是说，你有5000个mini-batch，因为5000乘以1000就是5000万。

你共有5000个mini-batch，所以最后得到是X^{5000}

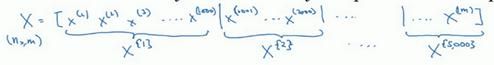
对Y也要进行相同处理，你也要相应地拆分Y的训练集，所以这是Y^{({1})，然后从y}((1001))到y^{((2000))，这个叫Y}({2})，一直到Y^({5000})。

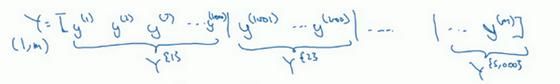
mini-batch的数量t组成了X^({t})和Y({t})，这就是1000个训练样本，包含相应的输入输出对。

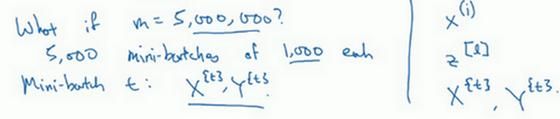
在继续课程之前，先确定一下我的符号，之前我们使用了上角小括号(i)表示训练集里的值，所以x^{((i))是第i个训练样本。我们用了上角中括号[l]来表示神经网络的层数，z}([l])表示神经网络中第l层的z值，我们现在引入了大括号t来代表不同的mini-batch，所以我们有X^({t})和Y({t})，检查一下自己是否理解无误。

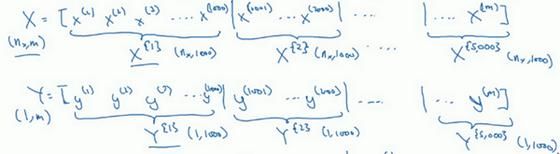
X^({t})和Y({t})的维数：如果X^{({1})是一个有1000个样本的训练集，或者说是1000个样本的x值，所以维数应该是(n_x,1000)，X}({2})的维数应该是(n_x,1000)，以此类推。因此所有的子集维数都是(n_x,1000)，而这些（Y^({t})）的维数都是(1,1000)。

解释一下这个算法的名称，batch梯度下降法指的是我们之前讲过的梯度下降法算法，就是同时处理整个训练集，这个名字就是来源于能够同时看到整个batch训练集的样本被处理，这个名字不怎么样，但就是这样叫它。

相比之下，mini-batch梯度下降法，指的是我们在下一张幻灯片中会讲到的算法，你每次同时处理的单个的mini-batch X^({t})和Y({t})，而不是同时处理全部的X和Y训练集。

那么究竟mini-batch梯度下降法的原理是什么？

在训练集上运行mini-batch梯度下降法，你运行for t=1……5000，因为我们有5000个各有1000个样本的组，在for循环里你要做得基本就是对X^({t})和Y({t})执行一步梯度下降法。假设你有一个拥有1000个样本的训练集，而且假设你已经很熟悉一次性处理完的方法，你要用向量化去几乎同时处理1000个样本。

首先对输入也就是X^{({t})，执行前向传播，然后执行z}([1])=W^([1]) X+b^{([1])，之前我们这里只有，但是现在你正在处理整个训练集，你在处理第一个mini-batch，在处理mini-batch时它变成了X}({t})，即z^([1])=W([1]) X^({t})+b([1])，然后执行A^([1]k)=g([1]) (Z^{([1]))，之所以用大写的Z是因为这是一个向量内涵，以此类推，直到A}([L])=g¹ (Z^([L]))，这就是你的预测值。

注意这里你需要用到一个向量化的执行命令，这个向量化的执行命令，一次性处理1000个而不是500万个样本。

接下来你要计算损失成本函数J，因为子集规模是1000，J=1/1000

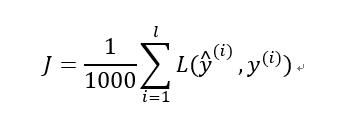
，说明一下，这（L(^y((i)),y^{((i)))）指的是来自于mini-batchX}({t})和Y^({t})中的样本。

如果你用到了正则化，你也可以使用正则化的术语:

，因为这是一个mini-batch的损失，所以我将J损失记为上角标t，放在大括号里

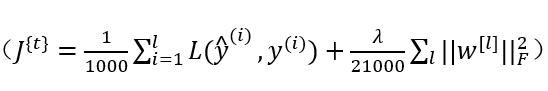
你也会注意到，我们做的一切似曾相识，其实跟之前我们执行梯度下降法如出一辙，除了你现在的对象不是X，Y，而是X^({t})和Y({t})。接下来，你执行反向传播来计算J^{({t})的梯度，你只是使用X}({t})和Y^({t})，然后你更新加权值，

W实际上是W^{([l])，更新为W}([l]):=W^([l])-adW([l])，

对b做相同处理，b^([l]):=b([l])-adb^([l])。

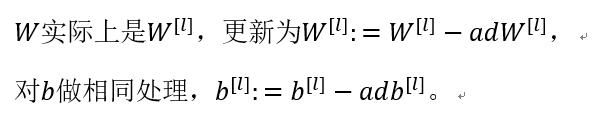
这是使用mini-batch梯度下降法训练样本的一步，我写下的代码也可被称为进行“一代”（1 epoch）的训练。一代这个词意味着只是一次遍历了训练集。

使用batch梯度下降法，一次遍历训练集只能让你做一个梯度下降，使用mini-batch梯度下降法，一次遍历训练集，能让你做5000个梯度下降。

当然正常来说你想要多次遍历训练集，还需要为另一个while循环设置另一个for循环。所以你可以一直处理遍历训练集，直到最后你能收敛到一个合适的精度。

如果你有一个丢失的训练集，mini-batch梯度下降法比batch梯度下降法运行地更快，

所以几乎每个研习深度学习的人在训练巨大的数据集时都会用到，下一个笔记中，我们将进一步深度讨论mini-batch梯度下降法，你也会因此更好地理解它的作用和原理。

---

1. L ↩︎