神经网络:ResNet 论文学习总结(二)-- 模型微调
引言
本片博客是对ResNet 网络模型的微调,论文链接,讲解链接。原始的ResNet结构在细节之处还有微调优化的空间,在论文《Bag of Tricks for Image Classification with Convolutional Neural Networks》中,作者从高效训练、模型微调、训练技巧三个方面给出了一些实践技巧。本文只讲模型微调部分,感兴趣可以继续阅读论文或阅读讲解链接的文章。
ResNet 网络结构的核心在于运用了 shortcut (原文称为 skip connection) 技术使得深层网络也能够被有效训练,具体细节可以参看上一篇博客 神经网络:ResNet 论文学习总结(一)
改进一:推迟下采样
该改进方法最初是在 Torch 上提出的,目前这一改进已经被广泛地应用。首先观察原始模型的下采样模块:
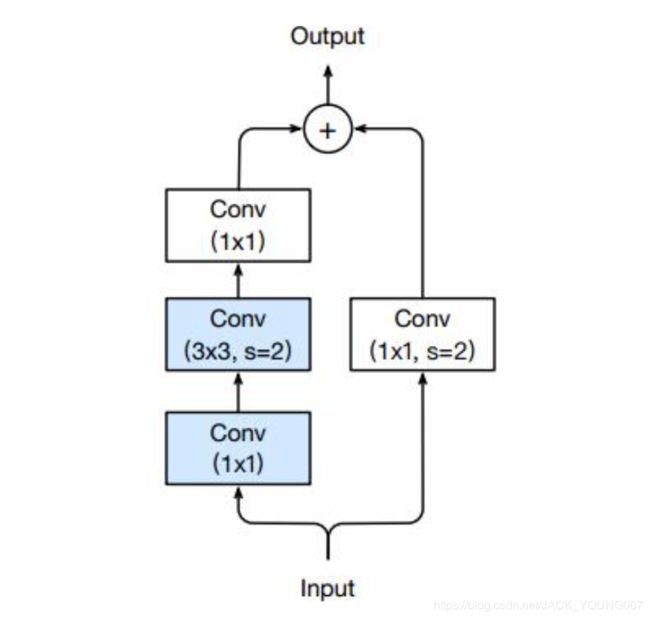
Path A 依次经过:
--1. 1x1的卷积,完成通道的收缩,并且步长为2以实现下采样
--2. 3x3的卷积,通道数不变,主要用于提取特征
--3. 1x1的卷积,完成通道数的扩张
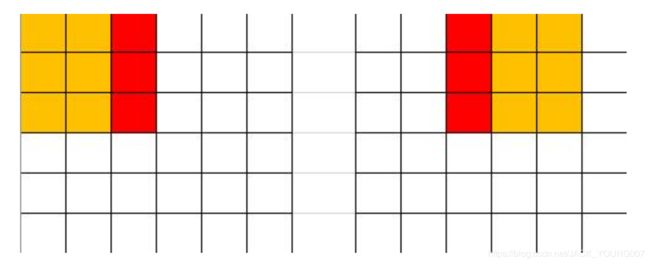
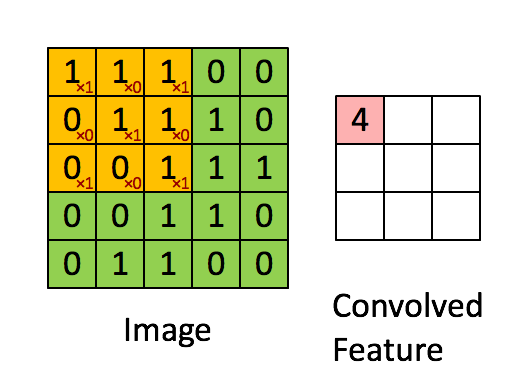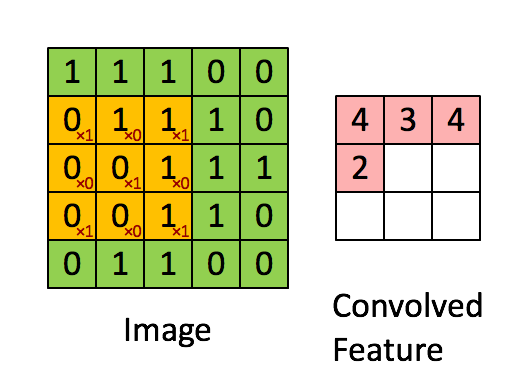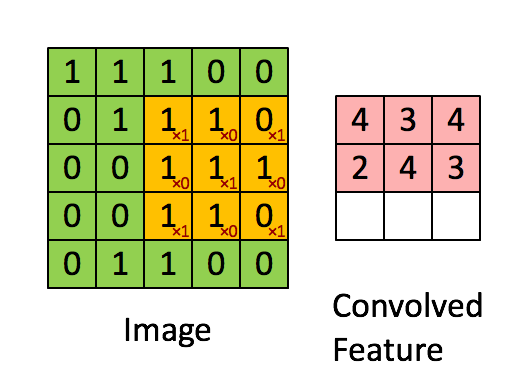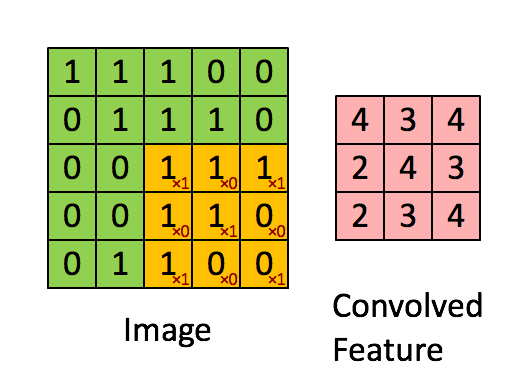
其中第一个卷积用来下采样,仔细思考会发现,核大小1x1、步长2的卷积会造成3/4 的信息丢失!以 6x6 的特征图为例,如下图,只有红色部分的信息才能够传递到下一层,非红色部分均不参与卷积运算。
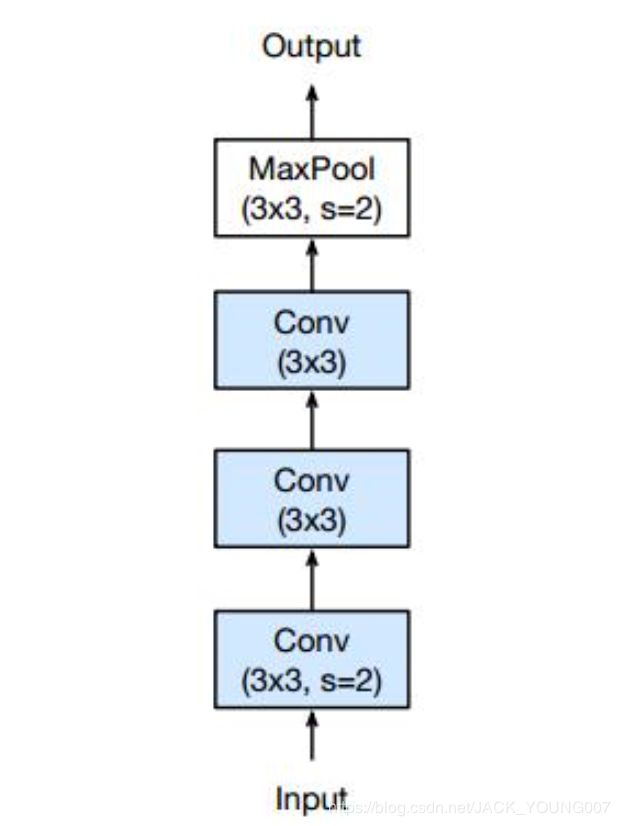
由此可见,在1x1 的卷积层做下采样是不明智的,更好的做法是把下采样过程挪到 3x3 的卷积上,如下图所示,由于卷积核宽度大于步长,卷积核在移动过程中能够遍历输入特征图上的所有信息,并且有一部分重叠。
下采样模块就变成了:
改进二:拆解大核卷积
大核卷积可以由多层小卷积核替代实现,这不仅可以减少参数,还能加深网络深度以实现网络容量和复杂度。讲解链接 Inception早在 《Rethinking the Inception Architecture for Computer Vision(2015)》一文中对 Inception 1 做出改进,分别用三个和两个 3x3 卷积的级联去替代 7x7 和 5x5 的卷积。
这一技巧同样适用于 ResNet 结构:
改进三:用平均池化替代 1x1 卷积做下采样
下采样模型的 PathA 和PathB 都需要做下采样才能正确的加和,改进一只针对 Path A 做了改进,其实 Path 也用了 1x1 的卷积核做下采样。为此,论文《Bag of Tricks for Image Classification with Convolutional Neural Networks(2018)》用平均池化代替了PathB 中的降采样工作:
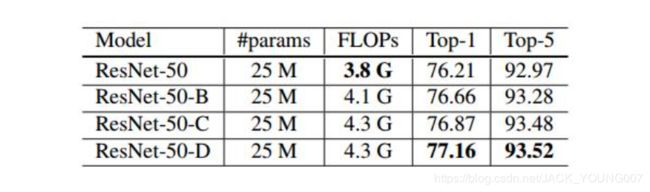
实验结果:
其中A、B、C、D分别代表原始、改进一、改进2、改进三的模型。经过改进之后,最终的 ResNet-50-D 准确率提高了 0.95%。但不得不承认的是,以上的改进都增加了模型的运算复杂度, FLOPs增加了约 13%,但实测速度却只下降了 3%。
关于 FLOPs 和实测速度
读者可能感到意外,为什么运算量明明增加了13%,可实测速度却只下降了 3%???
原因一:多分支网络
首先注意到是, ResNet 由于应用了 shortcut 技术,相比于传统的直筒式网络增加了分支,不同分支是可以并行计算的,而计算FLOPs 时却是把不同分支的运算量依次累加起来。
原因二:高效的 1x1 卷积
在 MobileNets 模型中可知:深度可分离卷积中的绝大数参数和运算都集中在 1x1 的 pointwise 卷积运算当中,这种运算恰恰是能够被 GEneral Matrix Multiply (GEMM)函数高度优化的。
为什么 1x1 卷积能够被高度优化?首先要从卷积计算的实现讲起:
卷积的原理:《动手学深度学习》参阅链接
首先考虑 3x3 的单通道特征图,以及kernelSize=2、stride=1、pad=0 的卷积核:
卷积计算:
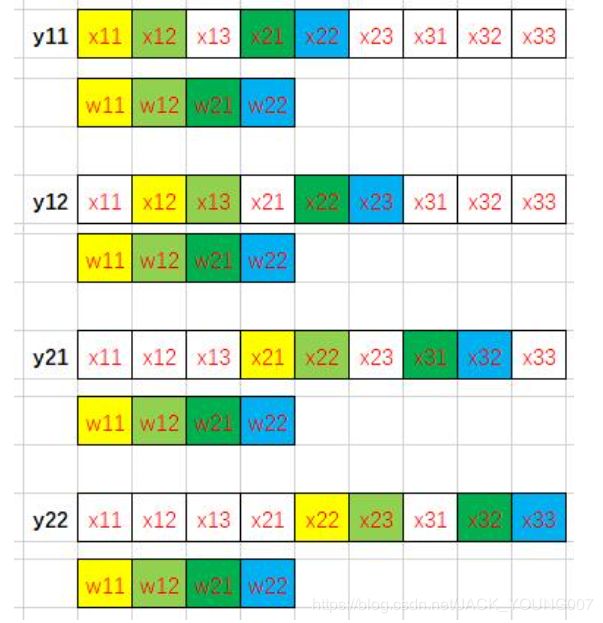
按照 “行先序”,特征图和卷积核在内存中是这样排列的:
用不同的颜色标注出卷积计算中的访存过程,相同颜色的数据相乘:
操作系统访存原理,由于程序的局部性(通常相邻代码段会访问相邻的内存块),现代处理器通常会按块从内存中读取数据到高速缓存中以缓解访存速度和计算速度的巨大差异导致的“内存墙”问题。换句话说,如果计算需要从内存中读取x12的数据,那么往往相邻的x11、x13等数据也会被一起读取到高速缓存上,当下次计算需要用到x11或x13时处理器就可以快速地从高速缓存中取出数据而不需要从内存中调取,大大提高了程序的速度。(L1 缓存的读取速度是 RAM的 50-100倍)
而从上边展示出来的访存过程中可以看到,直接对于特征图数据的访问过程十分散乱,直接用行先序存储的特征图参与计算是非常愚蠢的选择。因此深度学习框架往往通过牺牲空间的手段(约扩增K×KK×K倍),将特征图转换成庞大的矩阵来进行卷积计算,这就是常说的im2col操作。
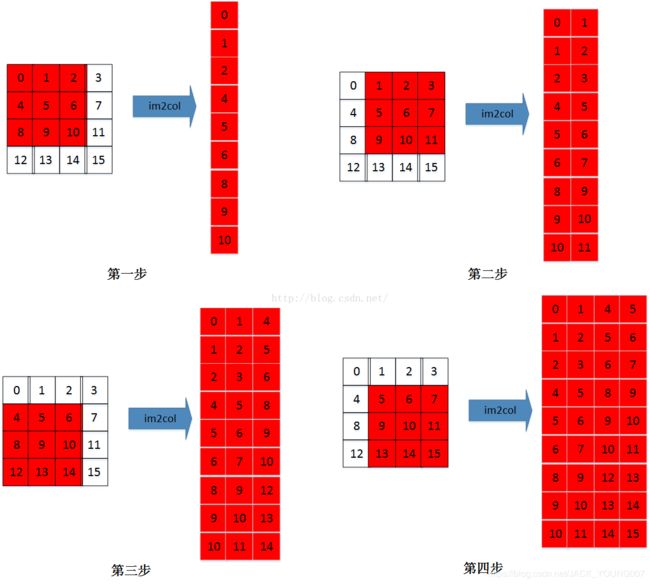
im2col 操作
其实思路非常简单:把每一次循环所需要的数据都排列成列向量,然后逐一堆叠起来形成矩阵(按通道顺序在列方向上拼接矩阵)。比如Ci×Wi×HiCi×Wi×Hi大小的输入特征图,K×KK×K大小的卷积核,输出大小为Co×Wo×HoCo×Wo×Ho,
输入特征图将按需求被转换成 (K∗K)×(Ci∗Wo∗Ho)(K∗K)×(Ci∗Wo∗Ho)的矩阵,卷积核将被转换成Co×(K∗K)Co×(K∗K)的矩阵,调用GEMM库两矩阵相乘也就完成了所谓的卷积计算。由于按照计算需求排布了数据顺序,每次计算过程中总是能够依次访问特征图数据,迎合了局部性原理,极大地提高了计算卷积的速度!
特别的 1x1
回到1x1的卷积,它的im2col非常特殊——其原始存储结构跟im2col的重排列矩阵是完全相同的!!也就是说,1x1卷积甚至不需要im2col的过程,拿起来就能直接算,节省了数据重排列的时间和空间,所以哪怕是在相同FLOPs的前提下,1x1卷积也要比3x3卷积快速、高效得多。当然,这是建立在局部性原理和冯诺依曼结构的基础之上,对于非冯结构的计算体系可能就不适用了。
这也是为什么MobileNet在论文最后要大肆鼓吹说他94.86%的运算量都集中1x1的卷积运算上,它的快速可不仅仅体现在“少参数,少运算量”上!
同理,前文中改进1和改进3看似增加了很多运算量,但这些运算量都是负担在1x1卷积上的,这就使得实测速度的下降远没有运算量增加那么明显!