软件工程基础个人项目——数独(5)

软件工程基础个人项目——数独

点击这里可看github上的具体代码
本次个人项目关于数独的生成与求解

PSP表格

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划
Estimate	估计这个任务需要多少时间	1520
Development	开发
Analysis	需求分析	20
Design Spec	生成设计文档	60
Design Review	设计复审
Coding Standard	代码规范
Design	具体设计	120
Coding	具体编码	600
Code Review	代码复审	200
Test	测试（自我测试，提交代码，代码修改）	400
Reporting	报告	30
Test Report	测试报告	30
Size Measurement	计算工作量	30
Postme & Process Improvement Plan	事后总结并提出过程改进计划	30
	合计	1520

思路描述

最开始看到题目的时候，感觉压力很大，因为在此之前我从未了解过数独，担心自己不能很好的理解数独，更不要说通过代码编写让计算机完成数独的求解和生成了。但是在网上是可以找到很多之前学姐学长们智慧的结晶，在本次个人项目上为我提供了很多帮助。我先从网上找寻了关于数独的有关内容，大致明白了数独的概念，也尝试的自己手动解了解数独。那么怎么更好的通过计算机实现数独的生成与求解呢。我看了很多相关博客，找到了我能理解也觉得比较简单的方法。
生成数独：先生成一个1-9的无重复的排列，再将此排列平移。除了第一行之外的每一行，都是通过第一行向右平移某位生成，出去的数字回到排列左端。
求解数独：
使用回溯方法，同时设立vis来确定是否可以将某数字放在某位置上，参考了之前某位学长或者学姐的博客，最终确定这个方法。

程序实现过程

数独的生成：
写一个函数Create_sudoku(),
这是我最开始的想法，后来为了方便管理，我写了一个class Sudo，在其中创建了create 函数。

数独的求解：
求解是solve函数，中心思想回溯由Traceback（）执行，其中设立的vis数组判断数字是否可以放在某位置上。需要setvis(),resetvis(),checkvis(),共同完成其功能。

设计图

Created with Raphaël 2.2.0 开始 打开文件 判断数独 打印一个数独 确认为0标记vis数组 对非0位置进行标记 回溯 关闭文件 结束 yes no yes

性能分析

进行数独的生成时，根据生成不同数量的数独的命令行进行分析，生成了不同的分析图。可能由于我把函数都写在一个大类中，进行分析时发现，时间占比最多的函数并不是我写的，而是存在于动态链接库中的函数。最终分析工具并没有指出函数名，显示说是调用堆栈的底部的函数

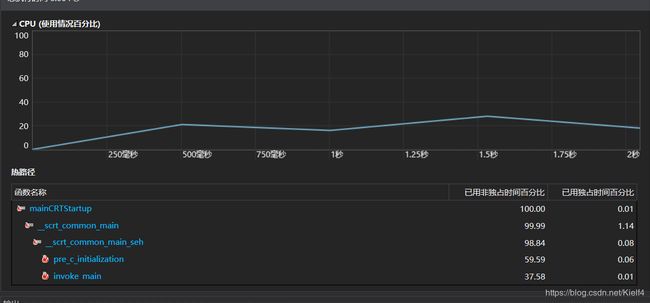
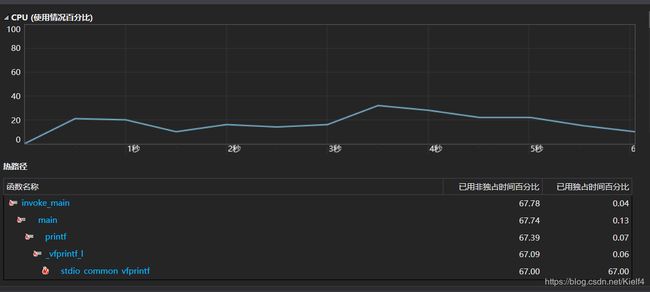
代码说明

主要是将运用的函数装在Sudo类里

class Sudo
{
	public:
		void create(int num);
		void solve(char* file);
		void setvis(int m, int n, int num);
		void resetvis(int m, int n, int num);
		bool checkvis(int m, int n, int num);
		void TraceBack(int n);
};

move对应的是以第一行为基准平移的位数可能情况的排列。13代表一到三行，36代表四到六行，69代表七到九行。

int a[15] = { '1','2','3','4','5','6','7','9' };//生成所用 
char move13[10][5] = { "036", "063" };
char move36[10][5] = { "258", "285", "528", "582", "825", "852" };
char move69[10][5] = { "147", "174", "417", "471", "714", "741" };

应有2 * 6* 6种可能，在每种可能下进行如下操作，最终生成这样一个数独

					for (int ii = 0;ii < 3;ii++)
					{
						move[rows] = move13[i][ii] - '0';
						rows++;
					}
					for (int jj = 0;jj < 3;jj++)
					{
						move[rows] = move36[j][jj] - '0';
						rows++;
					}
					for (int kk = 0;kk < 3;kk++)
					{
						move[rows] = move69[k][kk] - '0';
						rows++;
					}
					for (int l = 0;l < 9;l++)
					{
						int m = move[l];
						fputc(a[(8 + m) % 9], fout);
						for (int n = 1;n < 17;n++)
						{
							fputc(' ', fout);
							fputc(a[((16 - n) / 2 + m) % 9], fout);
							++n;
						}
						fputc('\n', fout);
					}

数独的求解部分，首先要判断数独，之后针对每一个数字字符，进行输入，组成矩阵数组，进行vis判断。最终进行回溯

	while (fscanf(fp1, "%d", &res[t / 9][t % 9]) != EOF)
	{
		if (count != 0)//代表数独数量 
		{
			sudokuu[p++] = '\n';
		}
		for (int t = 1;t < 81;t++)     //读入一个需要求解的数独
			fscanf(fp1, "%d", &res[t / 9][t % 9]);
		suc = 0;
		memset(vis, 0, sizeof(vis));
		for (int t = 0;t < 81;t++)
			if (res[t / 9][t % 9] != 0)   //当前格子有数字，跳到下一格
			{
				setvis(t / 9, t % 9, res[t / 9][t % 9]);
			}
		TraceBack(0);   //回溯求解
		count++;
	}

vis数组中的操作判断

void Sudo::setvis(int m, int n, int num)  //[m,n]有num，则vis对应为1 
{
	vis[0][m][num] = 1;
	vis[1][n][num] = 1;
	int nn;
	nn = m / 3 * 3 + n / 3;
	vis[2][nn][num] = 1;
}
void Sudo::resetvis(int m, int n, int num) //[m,n]无num,则vis对应为0 
{
	vis[0][m][num] = 0;
	vis[1][n][num] = 0;
	int nn;
	nn = m / 3 * 3 + n / 3;
	vis[2][nn][num] = 0;
}
bool Sudo::checkvis(int m, int n, int num)  //检查[m,n]中是否可放num 
{
	int nn;
	nn = m / 3 * 3 + n / 3;
	if (vis[0][m][num] == 0 && vis[1][n][num] == 0 && vis[2][nn][num] == 0)
		return true;
	else
		return false;
}

最终时间

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划
Estimate	估计这个任务需要多少时间	1520
Development	开发
Analysis	需求分析	20	30
Design Spec	生成设计文档	60	60
Design Review	设计复审
Coding Standard	代码规范
Design	具体设计	120	140
Coding	具体编码	600	700
Code Review	代码复审	200	150
Test	测试（自我测试，提交代码，代码修改）	400	400
Reporting	报告	30	50
Test Report	测试报告	30	50
Size Measurement	计算工作量	30	30
Postme & Process Improvement Plan	事后总结并提出过程改进计划	30	20
	合计	1520	1630

项目体会

这次作业我收获很大，随着自己的琢磨，向同学们进行了求助，也帮助了同学，非常开心。其实在考试周之前就开始进行了设计，但是比较大比重的工作都是在最后做的。这也是我第一次独立完成这种比较完整的工作，从设计到实现再到测试，收获很多。