机器学习中文参考手册
转自:http://wiki.opencv.org.cn/index.php/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0%E4%B8%AD%E6%96%87%E5%8F%82%E8%80%83%E6%89%8B%E5%86%8C
本文翻译尚未完成,请您将英文部分翻译为中文。
目录[隐藏]
|
简介:通用类和函数
机器学习库(MLL)是一些用于分类、回归和数据聚类的类和函数。
大部分分类和回归算法是用C++类来实现。尽管这些算法有一些不同的特性(像处理missing measurements的能力,或者categorical input variables等),这些类之间有一些相同之处。这些相同之处在类 CvStatModel 中被定义,其他 ML 类都是从这个类中继承。
CvStatModel
ML库中的统计模型基类。
class CvStatModel
{
public:
/* CvStatModel(); */
/* CvStatModel( const CvMat* train_data ... ); */
virtual ~CvStatModel();
virtual void clear()=0;
/* virtual bool train( const CvMat* train_data, [int tflag,] ..., const CvMat* responses, ...,
[const CvMat* var_idx,] ..., [const CvMat* sample_idx,] ...
[const CvMat* var_type,] ..., [const CvMat* missing_mask,] ... )=0;
*/
/* virtual float predict( const CvMat* sample ... ) const=0; */
virtual void save( const char* filename, const char* name=0 )=0;
virtual void load( const char* filename, const char* name=0 )=0;
virtual void write( CvFileStorage* storage, const char* name )=0;
virtual void read( CvFileStorage* storage, CvFileNode* node )=0;
};
在上面的声明中,一些函数被注释掉。实际上,一些函数没有一个单一的API(缺省的构造函数除外),然而,在本节后面描述的语法和定义方面有一些相似之处,好像他们是基类的一部分一样。
注意:opencv 1.0 版本对 CvStatModel 类做了修改,类的声明如下。
class CV_EXPORTS CvStatModel
{
public:
CvStatModel();
virtual ~CvStatModel();
virtual void clear();
virtual void save( const char* filename, const char* name=0 );
virtual void load( const char* filename, const char* name=0 );
virtual void write( CvFileStorage* storage, const char* name );
virtual void read( CvFileStorage* storage, CvFileNode* node );
protected:
const char* default_model_name;
};
CvStatModel::CvStatModel
缺省构造函数
CvStatModel::CvStatModel();
ML中的每个统计模型都有一个无参数构造函数。这个构造函数在"两步法"构造时非常有用,先调用这个缺省构造函数,紧接着调用 tranin() 或者load() 函数.(This constructor is useful for 2-stage model construction, when the default constructor is followed by train() or load().)
CvStatModel::CvStatModel(...)
训练构造函数
CvStatModel::CvStatModel( const CvMat* train_data ... ); */
大多数 ML 类都提供一个单步创建+训练的构造函数。此构造函数等价于缺省构造函数,加上一个紧接的 train() 方法调用,所传入的参数即为调用的参数。
CvStatModel::~CvStatModel
虚拟析构函数(Virtual destructor)
CvStatModel::~CvStatModel();
基类析构被声明为虚方法,因此你可以安全地写出下面的代码:
CvStatModel* model;
if( use_svm )
model = new CvSVM(... /* SVM params */);
else
model = new CvDTree(... /* Decision tree params */);
...
delete model;
一般,每个继承类的析构器不用做任何操作,但是如果调用了重载的clear()方法,将释放全部内存资源。
CvStatModel::clear
释放内存,重置模型状态
void CvStatModel::clear();
clear方法和析构函数发生的行为相似,比如:clear方法释放类成员所占用的内存空间。然而,和析构函数不同的是,clear方法不析构对象自身,也即调用clear方法后,对象本身在将来仍然可以使用。一般情况下,析构器、load方法、read方法、派生类train成员调用clear方法释放内存空间,甚至是用户也可以进行明确的调用。
CvStatModel::save
将模型保存到文件
void CvStatModel::save( const char* filename, const char* name=0 );
save方法将整个模型状态以指定名称或默认名称(取决于特定的类)保存到指定的XML或YAML文件中。该方法使用的是cxcore中的数据保存功能。
CvStatModel::load
从文件中装载模型
void CvStatModel::load( const char* filename, const char* name=0 );
load方法从指定的XML或YAML文件中装载指定名称(或默认的与模型相关名称)的整个模型状态。之前的模型状态将被clear()清零。
请注意,这个方法是虚的,因此任何模型都可以用这个虚方法来加载。然而,不像OpenCV中的C类型可以用通用函数cvLoad()来加载,这里模型类型无论如何都要是已知的,因为一个空模型作为恰当类的一种,必须被预先建构。这个限制将会在未来的ML版本中移除。
CvStatModel::write
将模型写入文件存储
void CvStatModel::write( CvFileStorage* storage, const char* name );
write方法将整个模型状态用指定的或默认的名称(取决于特定的类)写到文件存储中去。这个方法被save()调用。
CvStatModel::read
从文件存储中读出模型
void CvStatMode::read( CvFileStorage* storage, CvFileNode* node );
read方法从文件存储中的指定节点中读取整个模型状态。这个节点必须由用户来定位,如使用cvGetFileNodeByName()函数。这个方法被load()调用。
之前的模型状态被clear()清零。
CvStatModel::train
训练模型
bool CvStatMode::train( const CvMat* train_data, [int tflag,] ..., const CvMat* responses, ...,
[const CvMat* var_idx,] ..., [const CvMat* sample_idx,] ...
[const CvMat* var_type,] ..., [const CvMat* missing_mask,] ... );
这个函数利用输入的特征向量和对应的响应值(responses)来训练统计模型。特征向量和其对应的响应值都是用矩阵来表示。缺省情况下,特征向量都以行向量被保存在train_data中,也就是所有的特征向量元素都是连续存储。不过,一些算法可以处理转置表示,即特征向量用列向量来表示,所有特征向量的相同位置的元素连续存储。如果两种排布方式都支持,这个函数的参数tflag可以使用下面的取值:
- tflag=CV_ROW_SAMPLE
- 表示特征向量以行向量存储;
- tflag=CV_COL_SAMPLE
- 表示特征向量以列向量存储;
训练数据必须是32fC1(32位的浮点数,单通道)格式 响应值通常是以向量方式存储(一个行,或者一个列向量),存储格式为32sC1(仅在分类问题中)或者32fC1格式,每个输入特征向量对应一个值(虽然一些算法,比如某几种神经网络,响应值为向量)。
对于分类问题,响应值是离散的类别标签;对于回归问题,响应值是被估计函数的输出值。一些算法只能处理分类问题,一些只能处理回归问题,另一些算法这两类问题都能处理。In the latter case the type of output variable is either passed as separate parameter, or as a last element of var_type vector: CV_VAR_CATEGORICAL means that the output values are discrete class labels, CV_VAR_ORDERED(=CV_VAR_NUMERICAL) means that the output values are ordered, i.e. 2 different values can be compared as numbers, and this is a regression problem The types of input variables can be also specified using var_type. Most algorithms can handle only ordered input variables.
ML中的很多模型也可以仅仅使用选择特征的子集,或者(并且)使用选择样本的子集来训练。为了让用户易于使用,train函数通常包含var_idx和sample_idx参数。var_idx指定感兴趣的特征,sample_idx指定感兴趣的样本。这两个向量可以是整数(32sC1)向量,例如以0为开始的索引,或者8位(8uC1)的使用的特征或者样本的掩码。用户也可以传入NULL指针,用来表示训练中使用所有变量/样本。
除此之外,一些算法支持数据缺失情况,也就是某个训练样本的某个特征值未知(例如,他们忘记了在周一测量病人A的温度)。参数missing_mask,一个8位的同train_data同样大小的矩阵掩码,用来指示缺失的数据(掩码中的非零值)。
通常来说,在执行训练操作前,可以用clear()函数清除掉早先训练的模型状态。然而,一些函数可以选择用新的数据更新模型,而不是将模型重置,一切从头再来。
CvStatModel::predict
预测样本的response
float CvStatMode::predict( const CvMat* sample[,] ) const;
这个函数用来预测一个新样本的响应值(response)。在分类问题中,这个函数返回类别编号;在回归问题中,返回函数值。输入的样本必须与传给train_data的训练样本同样大小。如果训练中使用了var_idx参数,一定记住在predict函数中使用跟训练特征一致的特征。
后缀const是说预测不会影响模型的内部状态,所以这个函数可以很安全地从不同的线程调用。
Normal Bayes 分类器
这个简单的分类器模型是建立在每一个类别的特征向量服从正态分布的基础上的(尽管,不必是独立的),因此,整个分布函数被假设为一个高斯分布,每一类别一组系数。当给定了训练数据,算法将会估计每一个类别的向量均值和方差矩阵,然后根据这些进行预测。 [Fukunaga90] K. Fukunaga. Introduction to Statistical Pattern Recognition. second ed., New York: Academic Press, 1990.
注:OpenCV 1.0rc1(0.9.9)版本的贝叶斯分类器有个小bug, 训练数据时候会提示错误
OpenCV ERROR: Formats of input arguments do not match ()
in function cvSVD, cxsvd.cpp(1243)
修改方法为将文件 ml/src/mlnbayes.cpp 中的193行:
CV_CALL( cov = cvCreateMat( _var_count, _var_count, CV_32FC1 ));
改为
CV_CALL( cov = cvCreateMat( _var_count, _var_count, CV_64FC1 ));
此问题在OpenCV 1.0.0中已经得到修正。
CvNormalBayesClassifier
对正态分布的数据的贝叶斯分类器
class CvNormalBayesClassifier : public CvStatModel
{
public:
CvNormalBayesClassifier();
virtual ~CvNormalBayesClassifier();
CvNormalBayesClassifier( const CvMat* _train_data, const CvMat* _responses,
const CvMat* _var_idx=0, const CvMat* _sample_idx=0 );
virtual bool train( const CvMat* _train_data, const CvMat* _responses,
const CvMat* _var_idx = 0, const CvMat* _sample_idx=0, bool update=false );
virtual float predict( const CvMat* _samples, CvMat* results=0 ) const;
virtual void clear();
virtual void save( const char* filename, const char* name=0 );
virtual void load( const char* filename, const char* name=0 );
virtual void write( CvFileStorage* storage, const char* name );
virtual void read( CvFileStorage* storage, CvFileNode* node );
protected:
...
};
CvNormalBayesClassifier::train
训练这个模型
bool CvNormalBayesClassifier::train( const CvMat* _train_data, const CvMat* _responses,
const CvMat* _var_idx = 0, const CvMat* _sample_idx=0, bool update=false );
这个函数训练正态贝叶斯分类器。并且遵循通常训练“函数”的以下一些限制:只支持CV_ROW_SAMPLE类型的数据,输入的变量全部应该是有序的,输出的变量是一个分类结果。(例如,_responses中的元素必须是整数,因此向量的类型有可能是32fC1类型的),不支持missing, measurements。
另外,有一个update标志,标志着模型是否使用新数据升级。 In addition, there is update flag that identifies, whether the model should be trained from scratch (update=false) or be updated using the new training data (update=true).
CvNormalBayesClassifier::predict
对未知的样本或或本集进行预测
float CvNormalBayesClassifier::predict( const CvMat* samples, CvMat* results=0 ) const;
这个函数估计输入向量的最有可能的类别。输入向量(一个或多个)被储存在矩阵的每一行中。对于多个输入向量,则输出会是一个向量结果。对于单一的输入,函数本身的返回值就是预测结果。 长段文字
K近邻算法
这个算法首先贮藏所有的训练样本,然后通过分析(包括选举,计算加权和等方式)一个新样本周围K个最近邻以给出该样本的相应值。这种方法有时候被称作“基于样本的学习”,即为了预测,我们对于给定的输入搜索最近的已知其相应的特征向量。
CvKNearest
K近邻类
class CvKNearest : public CvStatModel //继承自ML库中的统计模型基类
{
public:
CvKNearest();
virtual ~CvKNearest(); //虚函数定义
CvKNearest( const CvMat* _train_data, const CvMat* _responses,
const CvMat* _sample_idx=0, bool _is_regression=false, int max_k=32 );
virtual bool train( const CvMat* _train_data, const CvMat* _responses,
const CvMat* _sample_idx=0, bool is_regression=false,
int _max_k=32, bool _update_base=false );
virtual float find_nearest( const CvMat* _samples, int k, CvMat* results,
const float** neighbors=0, CvMat* neighbor_responses=0, CvMat* dist=0 ) const;
virtual void clear();
int get_max_k() const;
int get_var_count() const;
int get_sample_count() const;
bool is_regression() const;
protected:
...
};
CvKNearest::train
训练KNN模型
bool CvKNearest::train( const CvMat* _train_data, const CvMat* _responses,
const CvMat* _sample_idx=0, bool is_regression=false,
int _max_k=32, bool _update_base=false );
这个类的方法训练K近邻模型。它遵循一个一般训练方法约定的限制:只支持CV_ROW_SAMPLE数据格式,输入向量必须都是有序的,而输出可以是 无序的(当is_regression=false),可以是有序的(is_regression=true)。并且变量子集和省略度量是不被支持的。
参数_max_k 指定了最大邻居的个数,它将被传给方法find_nearest。 参数 _update_base 指定模型是由原来的数据训练(_update_base=false),还是被新训练数据更新后再训练(_update_base=true)。在后一种情况下_max_k 不能大于原值, 否则它会被忽略.
CvKNearest::find_nearest
寻找输入向量的最近邻
float CvKNearest::find_nearest( const CvMat* _samples, int k, CvMat* results=0,
const float** neighbors=0, CvMat* neighbor_responses=0, CvMat* dist=0 ) const;
对每个输入向量(表示为matrix_sample的每一行),该方法找到k(k≤get_max_k() )个最近邻。在回归中,预测结果将是指定向量的近邻的响应的均值。在分类中,类别将由投票决定。
对传统分类和回归预测来说,该方法可以有选择的返回近邻向量本身的指针(neighbors, array of k*_samples->rows pointers),它们相对应的输出值(neighbor_responses, a vector of k*_samples->rows elements) ,和输入向量与近邻之间的距离(dist, also a vector of k*_samples->rows elements)。
对每个输入向量来说,近邻将按照它们到该向量的距离排序。
对单个输入向量,所有的输出矩阵是可选的,而且预测值将由该方法返回。In case of a single input vector all the output matrices are optional and the predicted value is returned by the method.
例程:使用kNN进行2维样本集的分类,样本集的分布为混合高斯分布
#include "ml.h"
#include "highgui.h"
int main( int argc, char** argv )
{
const int K = 10;
int i, j, k, accuracy;
float response;
int train_sample_count = 100;
CvRNG rng_state = cvRNG(-1);
CvMat* trainData = cvCreateMat( train_sample_count, 2, CV_32FC1 );
CvMat* trainClasses = cvCreateMat( train_sample_count, 1, CV_32FC1 );
IplImage* img = cvCreateImage( cvSize( 500, 500 ), 8, 3 );
float _sample[2];
CvMat sample = cvMat( 1, 2, CV_32FC1, _sample );
cvZero( img );
CvMat trainData1, trainData2, trainClasses1, trainClasses2;
// form the training samples
cvGetRows( trainData, &trainData1, 0, train_sample_count/2 );
cvRandArr( &rng_state, &trainData1, CV_RAND_NORMAL, cvScalar(200,200), cvScalar(50,50) );
cvGetRows( trainData, &trainData2, train_sample_count/2, train_sample_count );
cvRandArr( &rng_state, &trainData2, CV_RAND_NORMAL, cvScalar(300,300), cvScalar(50,50) );
cvGetRows( trainClasses, &trainClasses1, 0, train_sample_count/2 );
cvSet( &trainClasses1, cvScalar(1) );
cvGetRows( trainClasses, &trainClasses2, train_sample_count/2, train_sample_count );
cvSet( &trainClasses2, cvScalar(2) );
// learn classifier
CvKNearest knn( trainData, trainClasses, 0, false, K );
CvMat* nearests = cvCreateMat( 1, K, CV_32FC1);
for( i = 0; i < img->height; i++ )
{
for( j = 0; j < img->width; j++ )
{
sample.data.fl[0] = (float)j;
sample.data.fl[1] = (float)i;
// estimates the response and get the neighbors' labels
response = knn.find_nearest(&sample,K,0,0,nearests,0);
// compute the number of neighbors representing the majority
for( k = 0, accuracy = 0; k < K; k++ )
{
if( nearests->data.fl[k] == response)
accuracy++;
}
// highlight the pixel depending on the accuracy (or confidence)
cvSet2D( img, i, j, response == 1 ?
(accuracy > 5 ? CV_RGB(180,0,0) : CV_RGB(180,120,0)) :
(accuracy > 5 ? CV_RGB(0,180,0) : CV_RGB(120,120,0)) );
}
}
// display the original training samples
for( i = 0; i < train_sample_count/2; i++ )
{
CvPoint pt;
pt.x = cvRound(trainData1.data.fl[i*2]);
pt.y = cvRound(trainData1.data.fl[i*2+1]);
cvCircle( img, pt, 2, CV_RGB(255,0,0), CV_FILLED );
pt.x = cvRound(trainData2.data.fl[i*2]);
pt.y = cvRound(trainData2.data.fl[i*2+1]);
cvCircle( img, pt, 2, CV_RGB(0,255,0), CV_FILLED );
}
cvNamedWindow( "classifier result", 1 );
cvShowImage( "classifier result", img );
cvWaitKey(0);
cvReleaseMat( &trainClasses );
cvReleaseMat( &trainData );
return 0;
}
支持向量机部分
支持向量机(SVM),起初由vapnik提出时,是作为寻求最优(在一定程度上)二分类器的一种技术。后来它又被拓展到回归和聚类应用。SVM是一种基于核函数的方法,它通过某些核函数把特征向量映射到高维空间,然后建立一个线性判别函数(或者说是一个高维空间中的能够区分训练数据的最优超平面,参考异或那个经典例子)。假如SVM没有明确定义核函数,高维空间中任意两点距离就需要定义。
解是最优的在某种意义上是两类中距离分割面最近的特征向量和分割面的距离最大化。离分割面最近的特征向量被称为”支持向量”,意即其它向量不影响分割面(决策函数)。
有很多关于SVM的参考文献,这是两篇较好的入门文献。
【Burges98】 C. Burges. "A tutorial on support vector machines for pattern recognition", Knowledge Discovery and Data Mining 2(2), 1998. (available online at [1]).
LIBSVM - A Library for Support Vector Machines. By Chih-Chung Chang and Chih-Jen Lin ([2])
CvSVM
支持矢量机
class CvSVM : public CvStatModel //继承自基类CvStatModel
{
public:
// SVM type
enum { C_SVC=100, NU_SVC=101, ONE_CLASS=102, EPS_SVR=103, NU_SVR=104 };//SVC是SVM分类器,SVR是SVM回归
// SVM kernel type
enum { LINEAR=0, POLY=1, RBF=2, SIGMOID=3 }; //提供四种核函数,分别是线性,多项式,径向基,sigmoid型函数。
CvSVM();
virtual ~CvSVM();
CvSVM( const CvMat* _train_data, const CvMat* _responses,
const CvMat* _var_idx=0, const CvMat* _sample_idx=0,
CvSVMParams _params=CvSVMParams() );
virtual bool train( const CvMat* _train_data, const CvMat* _responses,
const CvMat* _var_idx=0, const CvMat* _sample_idx=0,
CvSVMParams _params=CvSVMParams() );
virtual float predict( const CvMat* _sample ) const;
virtual int get_support_vector_count() const;
virtual const float* get_support_vector(int i) const;
virtual void clear();
virtual void save( const char* filename, const char* name=0 );
virtual void load( const char* filename, const char* name=0 );
virtual void write( CvFileStorage* storage, const char* name );
virtual void read( CvFileStorage* storage, CvFileNode* node );
int get_var_count() const { return var_idx ? var_idx->cols : var_all; }
protected:
...
};
CvSVMParams
SVM训练参数struct
struct CvSVMParams
{
CvSVMParams();
CvSVMParams( int _svm_type, int _kernel_type,
double _degree, double _gamma, double _coef0,
double _C, double _nu, double _p,
CvMat* _class_weights, CvTermCriteria _term_crit );
int svm_type;
int kernel_type;
double degree; // for poly
double gamma; // for poly/rbf/sigmoid
double coef0; // for poly/sigmoid
double C; // for CV_SVM_C_SVC, CV_SVM_EPS_SVR and CV_SVM_NU_SVR
double nu; // for CV_SVM_NU_SVC, CV_SVM_ONE_CLASS, and CV_SVM_NU_SVR
double p; // for CV_SVM_EPS_SVR
CvMat* class_weights; // for CV_SVM_C_SVC
CvTermCriteria term_crit; // termination criteria
};
svm_type,SVM的类型:
- CvSVM::C_SVC - n(n>=2)分类器,允许用异常值惩罚因子C进行不完全分类。
- CvSVM::NU_SVC - n类似然不完全分类的分类器。参数nu取代了c,其值在区间【0,1】中,nu越大,决策边界越平滑。
- CvSVM::ONE_CLASS - 单分类器,所有的训练数据提取自同一个类里,然后SVM建立了一个分界线以分割该类在特征空间中所占区域和其它类在特征空间中所占区域。
- CvSVM::EPS_SVR - 回归。 训练集中的特征向量和拟合出来的超平面的距离需要小于p。异常值惩罚因子C被采用。
- CvSVM::NU_SVR - 回归;nu 代替了p
kernel_type//核类型:
- CvSVM::LINEAR - 没有任何向映射至高维空间,线性区分(或回归)在原始特征空间中被完成,这是最快的选择。 d(x,y) = x•y == (x,y)
- CvSVM::POLY - 多项式核: d(x,y) = (gamma*(x•y)+coef0)degree
- CvSVM::RBF - 径向基,对于大多数情况都是一个较好的选择:d(x,y) = exp(-gamma*|x-y|2)
- CvSVM::SIGMOID - sigmoid函数被用作核函数: d(x,y) = tanh(gamma*(x•y)+coef0)
degree, gamma, coef0:都是核函数的参数,具体的参见上面的核函数的方程。
C, nu, p:在一般的SVM优化求解时的参数。
class_weights:可选权重,赋给指定的类别。一般乘以C以后去影响不同类别的错误分类惩罚项。权重越大,某一类别的误分类数据的惩罚项就越大。
term_crit:SVM的迭代训练过程的中止。(解决了部分受约束二次最优问题)
该结构需要初始化,并传递给CvSVM的训练函数。
CvSVM::train
训练SVM
bool CvSVM::train( const CvMat* _train_data, const CvMat* _responses,
const CvMat* _var_idx=0, const CvMat* _sample_idx=0,
CvSVMParams _params=CvSVMParams() );
The method trains SVM model. It follows the conventions of generic train "method" with the following limitations: only CV_ROW_SAMPLE data layout is supported, the input variables are all ordered, the output variables can be either categorical (_params.svm_type=CvSVM::C_SVC or _params.svm_type=CvSVM::NU_SVC) or ordered (_params.svm_type=CvSVM::EPS_SVR or _params.svm_type=CvSVM::NU_SVR) or not required at all (_params.svm_type=CvSVM::ONE_CLASS), missing measurements are not supported.
所有的参数都被集成在CvSVMParams这个结构中。
CvSVM::get_support_vector*
得到支持矢量和特殊矢量的数
int CvSVM::get_support_vector_count() const; const float* CvSVM::get_support_vector(int i) const;
这个方法可以被用来得到支持矢量的集合。
补充:在WindowsXP+OpenCVRC1平台下整合OpenCV与libSVM
虽然从RC1版开始opencv开始增设ML类,提供对常见的分类器和回归算法的支持。但是尚存在一些问题,比如说例子少(官方许诺说很快会提供一批新例子,见CVS版)。单说SVM这种算法,它自己提供了一套比较完备的函数,但是并不见得优于老牌的libsvm(它也应该参考过libsvm,至于是否效率优于libsvm,我并没有作过测试,官方也没有什么说法,但是libsvm持续开源更新,是公认的现存的开源SVM库中最易上手,性能最好的库)。所以在你的程序里整合opencv和libSVM还是一种比较好的解决方案。在VC中整合有些小地方需要注意,这篇文档主要是提供把图象作为SVM输入时程序遇到的这些小问题的解决方案。希望大家遇到问题时,多去读libSVM的源码,它本身也是开源的,C代码写得也很优秀,数据结构定义得也比较好。
首先是SVM的训练,这部分我并没有整合到VC里,直接使用它提供的python程序,虽然网格搜索这种简易搜索也可以自己写,但是识别时只需要训练生成的SVMmodel文件即可,所以可以和主程序分离开。至于python在windows下的使用,还是要设置一下的,首先要在系统环境变量path里把python的路径设进去,libsvm画训练等高线图还需要gnuplot的支持,打开python源程序(grid.py),把gnuplot_exe设置成你机器里的安装路径,这样才能正确的运行程序。然后就是改步长和搜索范围,官方建议是先用大步长搜索,搜到最优值后再用小步长在小范围内搜索(我觉得这有可能会陷入局部最优,不过近似出的结果还可以接受)。我用的python版本是2.4,gnuplot4.0。
常用libSVM资料链接
官方站点,有一些tutorial和测试数据
哈工大的机器学习论坛,非常好(外网似乎不能登录)
上交的一个研究生还写过libsvm2.6版的代码中文注释,源链接找不着了,大家自己搜搜吧,写得很好,上海交通大学模式分析与机器智能实验室。 http://www.pami.sjtu.edu.cn/people/gpliu/
决策树
本节所讨论的 ML 类(s)实现了 [Brieman84] 中描述的分类与回归树算法。
类CvDTree可以表示一个单独使用的简单决策树,也可以表示树集成分类器中的一个基础分类器(参见Boosting和Random Trees)
决策树是一个二叉树(即树的非叶节点仅有两个子节点)。当每个叶节点用类别标识(多个叶子可能有相同的标识)时,它可以表示分类树;当每个叶节点被分配了一个常量(所以回归函数是分段常量)时,决策树就成了回归树。
用决策树进行预测
预测算法从根结点开始,到达某个叶结点,然后得到输入特征向量的响应。在每一个非叶子结点,算法会根据变量值选择向左走或者向右走(比如选择左子结点作为下一个观测结点),该变量的索引值储存在被观测结点中。这个变量可以是数值的或者类型的。如果变量是数值的,那么变量值就跟一个固定的阈值(也储存在被观测结点中)来比较,如果该变量小于阈值,那么算法就往左走,否则就往右(比如说,如果重量小于1kg,那么算法流程就往左走,否则就往右)。如果变量值是categorical的,那么这个离散变量值会被测试是否属于某个特定的子集(也储存在该结点中),这个子集取自于一个该变量可以取到的有限集合。如果变量属于该子集,那么算法流程就往左走,否则就往右(比如,如果颜色是绿色的或者红色的,就往左,否则就往右)。也就是说,在每个结点,使用一对实体对象(
To reach a leaf node, and thus to obtain a response for the input feature vector, the prediction procedure starts with the root node. From each non-leaf node the procedure goes to the left (i.e. selects the left child node as the next observed node), or to the right based on the value of a certain variable, which index is stored in the observed node. The variable can be either ordered or categorical. In the first case, the variable value is compared with the certain threshold (which is also stored in the node); if the value is less than the threshold, the procedure goes to the left, otherwise, to the right (for example, if the weight is less than 1 kilo, the procedure goes to the left, else to the right). And in the second case the discrete variable value is tested, whether it belongs to a certain subset of values (also stored in the node) from a limited set of values the variable could take; if yes, the procedure goes to the left, else - to the right (for example, if the color is green or red, go to the left, else to the right). That is, in each node, a pair of entities (
有时候,输入向量的某些特征缺失(比如说,在黑暗中很难去确定对象的颜色),而且预测算法可能在某一个结点上(在上面提到结点用色彩划分的例子里)反复运算。决策树用替代分裂点(surrogate splits)来避免这样的情况发生。这就是说,除了最佳初始分裂点(the best "primary" split)以外,每一个树结点可能都要被一个或多个几乎有一样的结果的变量分裂。
Sometimes, certain features of the input vector are missed (for example, in the darkness it is difficult to determine the object color), and the prediction procedure may get stuck in the certain node (in the mentioned example if the node is split by color). To avoid such situations, decision trees use so-called surrogate splits. That is, in addition to the best "primary" split, every tree node may also be split on one or more other variables with nearly the same results.
Training Decision Trees
训练决策树
决策树是从根结点递归构造的。用所有的训练数据(特征向量和对应的响应)来在根结点处进行分裂。在每个结点处,优化准则(比如最优分裂)是基于一些基本原则来确定的(比如ML中的“纯度purity”原则被用来进行分类,方差之和用来进行回归)。Then, if necessary, the surrogate splits are found that resemble at the most the results of the primary split on the training data; 所有的数据根据初始和替代分裂点来划分给左、右孩子结点(就像在预测算法里做的一样)。然后算法回归的继续分裂左右孩子结点。在以下情况下算法可能会在某个结点停止(i.e. stop splitting the node further):
- 树的深度达到了指定的最大值
- 在该结点训练样本的数目少于指定值,比如,没有统计意义上的集合来进一步进行结点分裂了。
- 在该结点所有的样本属于同一类(或者,如果是回归的话,变化已经非常小了)
- 跟随机选择相比,能选择到的最好的分裂已经基本没有什么有意义的改进了。
The tree is built recursively, starting from the root node. The whole training data (feature vectors and the responses) are used to split the root node. In each node the optimum decision rule (i.e. the best "primary" split) is found based on some criteria (in ML gini "purity" criteria is used for classification, and sum of squared errors is used for regression). Then, if necessary, the surrogate splits are found that resemble at the most the results of the primary split on the training data; all data are divided using the primary and the surrogate splits (just like it is done in the prediction procedure) between the left and the right child node. Then the procedure recursively splits both left and right nodes etc. At each node the recursive procedure may stop (i.e. stop splitting the node further) in one of the following cases:
- depth of the tree branch being constructed has reached the specified maximum value.
- number of training samples in the node is less than the specified threshold, i.e. it is not statistically representative set to split the node further.
- all the samples in the node belong to the same class (or, in case of regression, the variation is too small).
- the best split found does not give any noticeable improvement comparing to just a random choice.
当树建好之后,如果需要的话,可能需要用交叉验证来进行剪枝。这就是说,树的某些导致模型过拟合的分支将被剪掉。一般情况下,这个过程只用于单决策树上,因为tree ensembles通常会建立一些小的足够的树并且用他们自身的保护机制来防止过拟合。
When the tree is built, it may be pruned using cross-validation procedure, if need. That is, some branches of the tree that may lead to the model overfitting are cut off. Normally, this procedure is only applied to standalone decision trees, while tree ensembles usually build small enough trees and use their own protection schemes against overfitting.
“变量的重要性” Variable importance 决策树除了它的重要用途——预测以外,还可以用在多变量分析上。构造好的决策树算法的一个关键特性就是它可能被用在计算每个变量的重要性(相关决策力)上。举个例子,在一个垃圾邮件过滤器中,用一个经常出现在邮件中的词汇集合来作为特征向量,那么变量的重要率就可以用来决定最“垃圾邮件指示词”,这样就可以保证词汇集合的大小的合理性。
Besides the obvious use of decision trees - prediction, the tree can be also used for various data analysis. One of the key properties of the constructed decision tree algorithms is that it is possible to compute importance (relative decisive power) of each variable. For example, in a spam filter that uses a set of words occurred in the message as a feature vector, the variable importance rating can be used to determine the most "spam-indicating" words and thus help to keep the dictionary size reasonable.
每个变量的重要性的计算是在所有的在这个变量上的分裂进行的,不管是初始的还是替代的。这样的话,要准确计算变量重要性,即使没有缺失数据,替代分裂也必须包含在训练参数中。
Importance of each variable is computed over all the splits on this variable in the tree, primary and surrogate ones. Thus, to compute variable importance correctly, the surrogate splits must be enabled in the training parameters, even if there is no missing data.
[Brieman84] Breiman, L., Friedman, J. Olshen, R. and Stone, C. (1984), "Classification and Regression Trees", Wadsworth.
CvDTreeSplit
Decision tree node split
struct CvDTreeSplit
{
int var_idx;
int inversed;
float quality;
CvDTreeSplit* next;
union
{
int subset[2];
struct
{
float c;
int split_point;
}
ord;
};
};
- var_idx
- 分裂中所用到的变量的索引
- inversed
- 当等于1的时候,采用inverse split rule(比如,左分支和右分支在表达式下被交换)
- quality
- 分裂值,正数。用来选择最佳初始分裂点,然后用来对替代分裂点进行选择和排序。构造好树之后,还用来计算向量重要性
- next
- 指向结点分裂表中的下一个分裂点。
- subset
- 二值集合,用在在类别向量的分裂上。规则如下:如果var_value在subset里,那么next_node<-left,否则next_node<-right。
- c
-
用在数值变量的分裂上的阈值。规则如下:如果var_value
- split_point
- 用在训练算法内部。
- var_idx
- Index of the variable used in the split
- inversed
- When it equals to 1, the inverse split rule is used (i.e. left and right branches are exchanged in the expressions below)
- quality
- The split quality, a positive number. It is used to choose the best primary split, then to choose and sort the surrogate splits. After the tree is constructed, it is also used to compute variable importance.
- next
- Pointer to the next split in the node split list.
- subset
- Bit array indicating the value subset in case of split on a categorical variable. The rule is: if var_value in subset then next_node<-left else next_node<-right
- c
- The threshold value in case of split on an ordered variable. The rule is: if var_value < c then next_node<-left else next_node<-right
- split_point
- Used internally by the training algorithm.
CvDTreeNode
Decision tree node
struct CvDTreeNode
{
int class_idx;
int Tn;
double value;
CvDTreeNode* parent;
CvDTreeNode* left;
CvDTreeNode* right;
CvDTreeSplit* split;
int sample_count;
int depth;
...
};
- value
- 赋给结点的值。可以是一个类别标签,也可以是估计函数值。
- class_idx
- 赋给结点的归一化的类别索引(从 0到class_count-1 ),用在分类树和树集成中。
- Tn
- 在有序排列的树中的树索引。用在剪枝过程中和之后。在整棵树中根结点有最大的Tn值,子结点的Tn值小于或等于父结点,Tn≤CvDTree::pruned_tree_idx 的结点在预测阶段不予考虑(对应的分枝也被剪掉),即使它们还没有在物理上被从树上移除。
- parent, left, right
- 指向父结点、左右孩子结点的指针。
- split
- 指向第一个分裂点(初始分裂点)的指针。
- sample_count
- 在训练阶段所用到的样本数目。用来解决复杂的问题——当初始分裂点所用到的变量缺失时,而且其他替代分裂点所用到的变量也缺失时,如果left->sample_count>right->sample_count,那么样本直接进入左边的子结点,否则往右。
- depth
- 结点深度,根结点的深度是0,子结点的深度是父结点的深度加1。
CvDTreeNode的其他数据在训练阶段使用。
- value
- The value assigned to the tree node. It is either a class label, or the estimated function value.
- class_idx
- The assigned to the node normalized class index (to 0..class_count-1 range), it is used internally in classification trees and tree ensembles.
- Tn
- The tree index in a ordered sequence of trees. The indices are used during and after the pruning procedure. The root node has the maximum value Tn of the whole tree, child nodes have Tn less than or equal to the parent's Tn, and the nodes with Tn≤CvDTree::pruned_tree_idx are not taken into consideration at the prediction stage (the corresponding branches are considered as cut-off), even if they have not been physically deleted from the tree at the pruning stage.
- parent, left, right
- Pointers to the parent node, left and right child nodes.
- split
- Pointer to the first (primary) split.
- sample_count
- The number of samples that fall into the node at the training stage. It is used to resolve the difficult cases - when the variable for the primary split is missing, and all the variables for other surrogate splits are missing too, the sample is directed to the left if left->sample_count>right->sample_count and to the right otherwise.
- depth
- The node depth, the root node depth is 0, the child nodes depth is the parent's depth + 1.
Other numerous fields of CvDTreeNode are used internally at the training stage.
CvDTreeParams
Decision tree training parameters
struct CvDTreeParams
{
int max_categories;
int max_depth;
int min_sample_count;
int cv_folds;
bool use_surrogates;
bool use_1se_rule;
bool truncate_pruned_tree;
float regression_accuracy;
const float* priors;
CvDTreeParams() : max_categories(10), max_depth(INT_MAX), min_sample_count(10),
cv_folds(10), use_surrogates(true), use_1se_rule(true),
truncate_pruned_tree(true), regression_accuracy(0.01f), priors(0)
{}
CvDTreeParams( int _max_depth, int _min_sample_count,
float _regression_accuracy, bool _use_surrogates,
int _max_categories, int _cv_folds,
bool _use_1se_rule, bool _truncate_pruned_tree,
const float* _priors );
};
- max_depth
- 该参数指定树的最大可能深度。当某结点的深度小于max_depth时,训练算法将继续试图分裂该结点。如果满足了其他的终止准则,那么实际深度可能比max_depth小(参见本部门的训练过程),而且可能会被剪枝。
- min_sample_count
- 如果跟某结点相关的样本数量小于该参数值那么该结点就不被分裂。
- regression_accuracy
- 另一个终止准则——只用于回归树。一旦估计结点值与训练样本的响应的差小于该参数值,该结点就不再分裂。
- use_surrogates
- 如果该参数为真,替代结点就被建立。替代结点用在解决缺失数据和变量重要性估计。
- max_categories
- 在训练过程试图进行分裂时,如果一个离散变量比max_categories大,最佳精度子集的估计就需要花很长时间(比如算法是指数型的)。作为替代,许多决策树引擎(包括ML)试图通过把所有样本间聚成max_categories个类来找到最优子分裂点(比如,把一些类别聚到一起)。
- max_depth
- This parameter specifies the maximum possible depth of the tree. That is the training algorithms attempts to split a node while its depth is less than max_depth. The actual depth may be smaller if the other termination criteria are met (see the outline of the training procedure in the beginning of the section), and/or if the tree is pruned.
- min_sample_count
- A node is not split if the number of samples directed to the node is less than the parameter value.
- regression_accuracy
- Another stop criteria - only for regression trees. As soon as the estimated node value differs from the node training samples responses by less than the parameter value, the node is not split further.
- use_surrogates
- If true, surrogate splits are built. Surrogate splits are needed to handle missing measurements and for variable importance estimation.
- max_categories
- If a discrete variable, on which the training procedure tries to make a split, takes more than max_categories values, the precise best subset estimation may take a very long time (as the algorithm is exponential). Instead, many decision trees engines (including ML) try to find sub-optimal split in this case by clustering all the samples into max_categories clusters (i.e. some categories are merged together).
要注意到,这个技术只用于n(n>2)类分类问题上。在回归问题和2类分类问题上,不用聚类就可以有效地找到最优的分裂点,在这些情况下就不用这个参数。
- cv_folds
- 如果该参数>1,就用cv_folds——叠一交叉验证来进行剪枝。
- use_1se_rule
- 如果为真,就用剪枝算法减去树顶端的一些部分。这会让树变得紧致,而且对训练数据的噪声更有抵抗力一些,但是会牺牲一些精度。
- truncate_pruned_tree
- 如果为真,要被剪掉的结点(with Tn≤CvDTree::pruned_tree_idx)将被从树上移除。除非它们被保留,而且CvDTree::pruned_tree_idx(比如设该值为-1)递减,那么仍有可能从最初的没有被剪枝的树中获得结果。
- priors
- 类别先验概率的array,按类别标签值排序。该参数可以用在针对某个特定的类别而对决策树进行剪枝时。比如,如果用户希望探测到某个比较少见的异常变化,但训练可能包含了比异常多得多的正常情况,那么很可能分类结果就是认为每一个情况都是正常的。为了避免这一点,先验就必须被指定,异常情况发生的概率需要人为的增加(增加到0.5甚至更高),这样误分类的异常情况的权重就会变大,树也能够得到适当的调整。
Note that this technique is used only in N(>2)-class classification problems. In case of regression and 2-class classification the optimal split can be found efficiently without employing clustering, thus the parameter is not used in these cases.
- cv_folds
- If this parameter is >1, the tree is pruned using cv_folds-fold cross validation.
- use_1se_rule
- If true, the tree is truncated a bit more by the pruning procedure. That leads to compact, and more resistant to the training data noise, but a bit less accurate decision tree.
- truncate_pruned_tree
- If true, the cut off nodes (with Tn≤CvDTree::pruned_tree_idx) are physically removed from the tree. Otherwise they are kept, and by decreasing CvDTree::pruned_tree_idx (e.g. setting it to -1) it is still possible to get the results from the original unpruned (or pruned less aggressively) tree.
- priors
- The array of a priori class probabilities, sorted by the class label value. The parameter can be used to tune the decision tree preferences toward a certain class. For example, if users want to detect some rare anomaly occurrence, the training base will likely contain much more normal cases than anomalies, so a very good classification performance will be achieved just by considering every case as normal. To avoid this, the priors can be specified, where the anomaly probability is artificially increased (up to 0.5 or even greater), so the weight of the misclassified anomalies becomes much bigger, and the tree is adjusted properly.
关于内存管理:the field priors is a pointer to the array of floats。该列向量应该由用户指定分配,并且在CvDTreeParams这个结构传递给CvDTreeTrainData或者CvDTree构造函数或者方法(就像做了一个列向量的拷贝)之后进行释放。
- A note about memory management: the field priors is a pointer to the array of floats. The array should be allocated by user, and released just after the CvDTreeParams structure is passed to CvDTreeTrainData or CvDTree constructors/methods (as the methods make a copy of the array).
该结构包含了所有的决策树训练所需的参数。一个缺省的构造函数可以用缺省值来初始化所有的参数,构造一棵基本的分类树。任何参数都可以overridden,或者结构可以用构造函数的高级变量来进行完整的初始化。 The structure contains all the decision tree training parameters. There is a default constructor that initializes all the parameters with the default values tuned for standalone classification tree. Any of the parameters can be overridden then, or the structure may be fully initialized using the advanced variant of the constructor.
CvDTreeTrainData
Decision tree training data and shared data for tree ensembles
struct CvDTreeTrainData
{
CvDTreeTrainData();
CvDTreeTrainData( const CvMat* _train_data, int _tflag,
const CvMat* _responses, const CvMat* _var_idx=0,
const CvMat* _sample_idx=0, const CvMat* _var_type=0,
const CvMat* _missing_mask=0,
const CvDTreeParams& _params=CvDTreeParams(),
bool _shared=false, bool _add_labels=false );
virtual ~CvDTreeTrainData();
virtual void set_data( const CvMat* _train_data, int _tflag,
const CvMat* _responses, const CvMat* _var_idx=0,
const CvMat* _sample_idx=0, const CvMat* _var_type=0,
const CvMat* _missing_mask=0,
const CvDTreeParams& _params=CvDTreeParams(),
bool _shared=false, bool _add_labels=false,
bool _update_data=false );
virtual void get_vectors( const CvMat* _subsample_idx,
float* values, uchar* missing, float* responses, bool get_class_idx=false );
virtual CvDTreeNode* subsample_data( const CvMat* _subsample_idx );
virtual void write_params( CvFileStorage* fs );
virtual void read_params( CvFileStorage* fs, CvFileNode* node );
// release all the data
virtual void clear();
int get_num_classes() const;
int get_var_type(int vi) const;
int get_work_var_count() const;
virtual int* get_class_labels( CvDTreeNode* n );
virtual float* get_ord_responses( CvDTreeNode* n );
virtual int* get_labels( CvDTreeNode* n );
virtual int* get_cat_var_data( CvDTreeNode* n, int vi );
virtual CvPair32s32f* get_ord_var_data( CvDTreeNode* n, int vi );
virtual int get_child_buf_idx( CvDTreeNode* n );
////////////////////////////////////
virtual bool set_params( const CvDTreeParams& params );
virtual CvDTreeNode* new_node( CvDTreeNode* parent, int count,
int storage_idx, int offset );
virtual CvDTreeSplit* new_split_ord( int vi, float cmp_val,
int split_point, int inversed, float quality );
virtual CvDTreeSplit* new_split_cat( int vi, float quality );
virtual void free_node_data( CvDTreeNode* node );
virtual void free_train_data();
virtual void free_node( CvDTreeNode* node );
int sample_count, var_all, var_count, max_c_count;
int ord_var_count, cat_var_count;
bool have_labels, have_priors;
bool is_classifier;
int buf_count, buf_size;
bool shared;
CvMat* cat_count;
CvMat* cat_ofs;
CvMat* cat_map;
CvMat* counts;
CvMat* buf;
CvMat* direction;
CvMat* split_buf;
CvMat* var_idx;
CvMat* var_type; // i-th element =
// k<0 - ordered
// k>=0 - categorical, see k-th element of cat_* arrays
CvMat* priors;
CvDTreeParams params;
CvMemStorage* tree_storage;
CvMemStorage* temp_storage;
CvDTreeNode* data_root;
CvSet* node_heap;
CvSet* split_heap;
CvSet* cv_heap;
CvSet* nv_heap;
CvRNG rng;
};
这个结构体通常有效的用在存储单树和决策树集成中。通常包含3类信息:
- 训练参数,CvDTreeParams instance。
- 训练数据,通常为了有效地找到最佳分裂点,需要被预处理。对树集成来说,被预处理后的数据要反复用在所有的树中。另外,训练数据特征为树集成中的所有的树所共享,并如下储存:变量类型,类别数,类别标签压缩图等。
- Buffers,树结点、分裂点和其他树结构元素的内存储存
有两种使用该结构的方式。在一些简单的情况下(比如,单树,或者从ML中得到的黑盒子树集成,如随机树或者boosting),这就没有需要去注意甚至了解这个结构——只要去构建需要的统计模型,训练并使用就行了。CvDTreeTrainData这个结构体可以在内部构建和使用。但是,对传统的树算法或者其他一些复杂的情况来说,这个结构体就必须被精确的构建和使用,如下所示:
- 结构体需要在set_data之后用缺省构造函数初始化(或者用完整的构造函数构建)。参数_shared设置为true。
- 用这个数据训练一棵或者多棵树,具体见方法CvDTree:train。
- 最后,该结构体只能在所有使用它的树被释放后释放。
This structure is mostly used internally for storing both standalone trees and tree ensembles efficiently. Basically, it contains 3 types of information
- The training parameters, CvDTreeParams instance.
- The training data, preprocessed in order to find the best splits more efficiently. For tree ensembles this preprocessed data is reused by all the trees. Additionally, the training data characteristics that are shared by all trees in the ensemble are stored here: variable types, the number of classes, class label compression map etc.
- Buffers, memory storages for tree nodes, splits and other elements of the trees constructed.
There are 2 ways of using this structure. In simple cases (e.g. standalone tree, or ready-to-use "black box" tree ensemble from ML, like Random Trees or Boosting) there is no need to care or even to know about the structure - just construct the needed statistical model, train it and use it. The CvDTreeTrainData structure will be constructed and used internally. However, for custom tree algorithms, or another sophisticated cases, the structure may be constructed and used explicitly. The scheme is the following:
- The structure is initialized using the default constructor, followed by set_data (or it is built using the full form of constructor). The parameter _shared must be set to true.
- One or more trees are trained using this data, see the special form of the method CvDTree::train.
- Finally, the structure can be released only after all the trees using it are released.
CvDTree
Decision tree
class CvDTree : public CvStatModel
{
public:
CvDTree();
virtual ~CvDTree();
virtual bool train( const CvMat* _train_data, int _tflag,
const CvMat* _responses, const CvMat* _var_idx=0,
const CvMat* _sample_idx=0, const CvMat* _var_type=0,
const CvMat* _missing_mask=0,
CvDTreeParams params=CvDTreeParams() );
virtual bool train( CvDTreeTrainData* _train_data, const CvMat* _subsample_idx );
virtual CvDTreeNode* predict( const CvMat* _sample, const CvMat* _missing_data_mask=0,
bool raw_mode=false ) const;
virtual const CvMat* get_var_importance();
virtual void clear();
virtual void read( CvFileStorage* fs, CvFileNode* node );
virtual void write( CvFileStorage* fs, const char* name );
// special read & write methods for trees in the tree ensembles
virtual void read( CvFileStorage* fs, CvFileNode* node,
CvDTreeTrainData* data );
virtual void write( CvFileStorage* fs );
const CvDTreeNode* get_root() const;
int get_pruned_tree_idx() const;
CvDTreeTrainData* get_data();
protected:
virtual bool do_train( const CvMat* _subsample_idx );
virtual void try_split_node( CvDTreeNode* n );
virtual void split_node_data( CvDTreeNode* n );
virtual CvDTreeSplit* find_best_split( CvDTreeNode* n );
virtual CvDTreeSplit* find_split_ord_class( CvDTreeNode* n, int vi );
virtual CvDTreeSplit* find_split_cat_class( CvDTreeNode* n, int vi );
virtual CvDTreeSplit* find_split_ord_reg( CvDTreeNode* n, int vi );
virtual CvDTreeSplit* find_split_cat_reg( CvDTreeNode* n, int vi );
virtual CvDTreeSplit* find_surrogate_split_ord( CvDTreeNode* n, int vi );
virtual CvDTreeSplit* find_surrogate_split_cat( CvDTreeNode* n, int vi );
virtual double calc_node_dir( CvDTreeNode* node );
virtual void complete_node_dir( CvDTreeNode* node );
virtual void cluster_categories( const int* vectors, int vector_count,
int var_count, int* sums, int k, int* cluster_labels );
virtual void calc_node_value( CvDTreeNode* node );
virtual void prune_cv();
virtual double update_tree_rnc( int T, int fold );
virtual int cut_tree( int T, int fold, double min_alpha );
virtual void free_prune_data(bool cut_tree);
virtual void free_tree();
virtual void write_node( CvFileStorage* fs, CvDTreeNode* node );
virtual void write_split( CvFileStorage* fs, CvDTreeSplit* split );
virtual CvDTreeNode* read_node( CvFileStorage* fs, CvFileNode* node, CvDTreeNode* parent );
virtual CvDTreeSplit* read_split( CvFileStorage* fs, CvFileNode* node );
virtual void write_tree_nodes( CvFileStorage* fs );
virtual void read_tree_nodes( CvFileStorage* fs, CvFileNode* node );
CvDTreeNode* root;
int pruned_tree_idx;
CvMat* var_importance;
CvDTreeTrainData* data;
};
CvDTree::train
Trains decision tree
bool CvDTree::train( const CvMat* _train_data, int _tflag,
const CvMat* _responses, const CvMat* _var_idx=0,
const CvMat* _sample_idx=0, const CvMat* _var_type=0,
const CvMat* _missing_mask=0,
CvDTreeParams params=CvDTreeParams() );
bool CvDTree::train( CvDTreeTrainData* _train_data, const CvMat* _subsample_idx );
在CvDTree中一共有两种训练方法。 第一种方法从基类CvStatModel::train而来,很完整。支持所有的数据方式(_tflag=CV_ROW_SAMPLE and _tflag=CV_COL_SAMPLE),同时还有样本和变量子集,缺失数据(missing measurements),输入和输出的变量类型的人工合并等。最后一个参数包含所有必须的训练参数,具体参见CvDTreeParams的描述。
第二种训练方法最多的是用在构建树集成。它采用了预构造的CvDTreeTrainData instance和训练集合的可选择子集。_subsample_idx的索引值与_sample_indx相关,并传递给CvDTreeTrainData构造函数。比如,如果_sample_idx=[1,5,7,100],那么_subsample_idx=[0,3]就表示样本原始样本集合的[1,100]被使用。
There are 2 train methods in CvDTree.
The first method follows the generic CvStatModel::train conventions, it is the most complete form of it. Both data layouts (_tflag=CV_ROW_SAMPLE and _tflag=CV_COL_SAMPLE) are supported, as well as sample and variable subsets, missing measurements, arbitrary combinations of input and output variable types etc. The last parameter contains all the necessary training parameters, see CvDTreeParams description.
The second method train is mostly used for building tree ensembles. It takes the pre-constructed CvDTreeTrainData instance and the optional subset of training set. The indices in _subsample_idx are counted relatively to the _sample_idx, passed to CvDTreeTrainData constructor. For example, if _sample_idx=[1, 5, 7, 100], then _subsample_idx=[0,3] means that the samples [1, 100] of the original training set are used.
CvDTree::predict
返回输入向量对应的叶子结点。
Returns the leaf node of decision tree corresponding to the input vector
CvDTreeNode* CvDTree::predict( const CvMat* _sample, const CvMat* _missing_data_mask=0,
bool raw_mode=false ) const;
该方法用特征向量和可选的缺失数据的掩模作为输入,在决策树计算之后,用到达的叶子结点作为输出。预测结果,无论是类别标签还是预测函数值,都在CvDTreeNode结构体中找到,比如,dtree->predict(sample,mask)->value。
最后一个参数通常设置为false,这样就表示正常的输入。如果为true,该方法就假定所有的离散输入变量值都已经归一化到0
例子,对Mushroom构建树进行分类
见mushroom.cpp,演示了怎样构建和使用决策树。
The method takes the feature vector and the optional missing measurement mask on input, traverses the decision tree and returns the reached leaf node on output. The prediction result, either the class label or the estimated function value, may be retrieved as value field of the CvDTreeNode structure, for example: dtree->predict(sample,mask)->value
The last parameter is normally set to false that implies a regular input. If it is true, the method assumes that all the values of the discrete input variables have been already normalized to 0..
See mushroom.cpp sample that demonstrates how to build and use the decision tree.
Boosting
一般的机器学习方法是监督学习方法:训练数据由输入和期望的输出组成,然后对非训练数据进行预测输出,也就是找出输入x与输出y之间的函数关系F: y = F(x)。根据输出的精确特性又可以分为分类和回归。
Boosting 是个非常强大的学习方法, 它也是一个监督的分类学习方法。它组合许多“弱”分类器来产生一个强大的分类器组[HTF01]。一个弱分类器的性能只是比随机选择好一点,因此它可以被设计的非常简单并且不会有太大的计算花费。将很多弱分类器结合起来组成一个集成的类似于SVM或者神经网络的强分类器。
在设计boosting分类器的时候最常用的弱分类器是决策树。通常每个树只具有一个节点的这种最简单的决策树就足够了。
Boosting模型的学习时间里在N个训练样本{(xi,yi)}1N 其中 xi ∈ RK 并且 yi ∈ {−1, +1}。xi是一个K维向量。每一维对应你所要分类的问题中的一个特征。输出的两类为-1和+1。
几种不同的boosting如离散AdaBoost, 实数AdaBoost, LogitBoost和Gentle AdaBoost[FHT98]。它们有非常类似的总体结构。因此,我们只需要了解下面表格中最基础的两类:离散AdaBoost和实数Adaboost算法。为每一个样本初始化使它们具有相同的权值(step 2)。然后一个弱分类器f(x)在具有权值的训练数据上进行训练。计算错误率和换算系数cm(step 3b). 被错分的样本的权重会增加。所有的权重进行归一化,并继续寻找若其他分类器M-1次。最后得到的分类器F(x)是这些独立的弱分类器的和的符号函数(step 4)。
- 给定N样本 (xi,yi) 其中
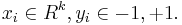
- 初始化权值
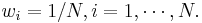
- 重复 for m = 1,2,…,M:
- 根据每个训练数据的wi计算
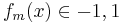 。
。 - 计算
![err_m = E_w [1(y \neq f_m(x))], c_m = \log((1 - err_m)/err_m)](http://img.e-com-net.com/image/info8/273506e93b39411dad69ecfaac408ce4.png) .
. - 更新权值
![w_i \leftarrow w_i \exp[c_m 1(y_i \neq f_m(x_i))], i = 1,2,\cdots,N](http://img.e-com-net.com/image/info8/2c448e7ab89f48d6b422847780ce960b.png) , 并归一化使 Σiwi = 1.
, 并归一化使 Σiwi = 1.
- 根据每个训练数据的wi计算
- 输出分类器
![sign[\Sigma_{m = 1}^M c_m f_m(x)]](http://img.e-com-net.com/image/info8/68e8de71caaa4220ac33fbfbb9cdaa73.png) .
.
两类问题的算法:训练(step 1~3)和估计(step 4)
注意:作为传统的boosting算法,上述的算法只可以解决两类问题。对于多类的分类问题可以使用AdaBoost.MH算法将其简化为两类分类的问题,但同时需要较大的训练数据,可以在[FHT98]中找到相应的说明。
为了减少计算的时间复杂度而不减少精度,可以使用influence trimming方法。随着训练算法的进行和集合中树的数量的增加和信任度的增加,大部分的训练数据被正确的分类,从而这些样本的权重不断的降低。具有较低相关权重的样本对弱分类器的训练有较低的影响。因此这些样本会在训练分类器时排除在外而不对分类器造成较大影响。控制这个过程的参数是weight_trim_rate。只有样本的每小部分的weight_trim_rate的总和较大时才会被用于弱分类器的训练。注意每个样本的系数在每个循环中被重新计算。一些已经删除的样本可能会在训练更多的分类器时被再次使用。[FHT98].
[HTF01] Hastie, T., Tibshirani, R., Friedman, J. H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer Series in Statistics. 2001.
[FHT98] Friedman, J. H., Hastie, T. and Tibshirani, R. Additive Logistic Regression: a Statistical View of Boosting. Technical Report, Dept. of Statistics, Stanford University, 1998.
CvBoostParams
Boosting 训练参数
struct CvBoostParams : public CvDTreeParams
{
int boost_type;
int weak_count;
int split_criteria;
double weight_trim_rate;
CvBoostParams();
CvBoostParams( int boost_type, int weak_count, double weight_trim_rate,
int max_depth, bool use_surrogates, const float* priors );
};
- boost_type
- Boosting type, 下面的一种
- CvBoost::DISCRETE - 离散 AdaBoost
- CvBoost::REAL - 实数 AdaBoost
- CvBoost::LOGIT - LogitBoost
- CvBoost::GENTLE - Gentle AdaBoost
- Gentle AdaBoost 和实数 AdaBoost 是最经常的选择。
- weak_count
- 建立的弱分类器的个数。
- split_criteria
- 分裂准则, 用以为弱分类树选择最优的分裂系数。构造函数:
- CvBoost::DEFAULT - 为特定的boosting算法选择默认系数;见下文。
- CvBoost::GINI - 使用 Gini 索引。这是实数AdaBoost的默认方法; 也可以被用做离散AdaBoost。
- CvBoost::MISCLASS - 使用误分类速率。这是离散AdaBoost的默认方法; 也可以被用做实数AdaBoost。
- CvBoost::SQERR - 使用最小二乘准则. 这是LogitBoost和Gentle AdaBoost的默认选择和唯一选择。
- weight_trim_rate
- The weight trimming ratio, 在0到1之间,参考上面的讨论。 如果这个系数小于等于0或者大于1,那么这个trimming将不会被使用,所有的样本都会在每个循环中使用。其默认值为0.95
这个结构从CvDTreeParams继承,但不是所有的决策树参数都支持。特别的,cross-validation不被支持。
CvBoostTree
弱分类树
class CvBoostTree: public CvDTree
{
public:
CvBoostTree();
virtual ~CvBoostTree();
virtual bool train( CvDTreeTrainData* _train_data,
const CvMat* subsample_idx, CvBoost* ensemble );
virtual void scale( double s );
virtual void read( CvFileStorage* fs, CvFileNode* node,
CvBoost* ensemble, CvDTreeTrainData* _data );
virtual void clear();
protected:
...
CvBoost* ensemble;
};
作为一个boost树分类器CvBoost的组成部分,这个弱分类器是从CvDTree派生得来的。通常,不需要直接使用弱分类器,虽然它们可以作为CvBoost::weak的元素序列通过CvBoost::get_weak_predictions来访问。
注意:在LogitBoost和Gentle AdaBoost的情况下,每一个若预测器是一个递归树,而不是分类树。甚至在离散AdaBoost和实数AdaBoost的情况下,CvBoost::predict的返回值(CvDTreeNode::value)也不是输出的类别标号;一个负数代表为类别#0,一个正数代表类别#1。而这些数只是权重。每一个独立的树的权重可以通过函数CvBoostTree::scale增加或减少。
CvBoost
Boost树分类器
class CvBoost : public CvStatModel
{
public:
// Boosting type
enum { DISCRETE=0, REAL=1, LOGIT=2, GENTLE=3 };
// Splitting criteria
enum { DEFAULT=0, GINI=1, MISCLASS=3, SQERR=4 };
CvBoost();
virtual ~CvBoost();
CvBoost( const CvMat* _train_data, int _tflag,
const CvMat* _responses, const CvMat* _var_idx=0,
const CvMat* _sample_idx=0, const CvMat* _var_type=0,
const CvMat* _missing_mask=0,
CvBoostParams params=CvBoostParams() );
virtual bool train( const CvMat* _train_data, int _tflag,
const CvMat* _responses, const CvMat* _var_idx=0,
const CvMat* _sample_idx=0, const CvMat* _var_type=0,
const CvMat* _missing_mask=0,
CvBoostParams params=CvBoostParams(),
bool update=false );
virtual float predict( const CvMat* _sample, const CvMat* _missing=0,
CvMat* weak_responses=0, CvSlice slice=CV_WHOLE_SEQ,
bool raw_mode=false ) const;
virtual void prune( CvSlice slice );
virtual void clear();
virtual void write( CvFileStorage* storage, const char* name );
virtual void read( CvFileStorage* storage, CvFileNode* node );
CvSeq* get_weak_predictors();
const CvBoostParams& get_params() const;
...
protected:
virtual bool set_params( const CvBoostParams& _params );
virtual void update_weights( CvBoostTree* tree );
virtual void trim_weights();
virtual void write_params( CvFileStorage* fs );
virtual void read_params( CvFileStorage* fs, CvFileNode* node );
CvDTreeTrainData* data;
CvBoostParams params;
CvSeq* weak;
...
};
CvBoost::train
训练boost树分类器
bool CvBoost::train( const CvMat* _train_data, int _tflag,
const CvMat* _responses, const CvMat* _var_idx=0,
const CvMat* _sample_idx=0, const CvMat* _var_type=0,
const CvMat* _missing_mask=0,
CvBoostParams params=CvBoostParams(),
bool update=false );
这个分类函数使用的是最通常的模板,最后一个参数update表示分类器是否需要更新(例如,新的弱分类树是否被加入到已存在的总和里), 或者是分类器是否需要重新建立。返回必须是类别,boost树不能用于递归的建立,且必须是两类。 注:如_train_data的维数是data_number*featureDim,则_responses的维数为data_number*1,_var_type的维数为featureDim+1*1,也就是说_var_type的维数是特征维数+1。并且,训练样本的样本数有一定的限制,样本的个数最低为10个,否则会报错。
CvBoost::predict
预测对输入样本的响应
float CvBoost::predict( const CvMat* sample, const CvMat* missing=0,
CvMat* weak_responses=0, CvSlice slice=CV_WHOLE_SEQ,
bool raw_mode=false ) const;
- sample
- 输入样本。
- missing
- 输入的sample中可能存在一些缺少的测量(即一部分测量可能没有观测到),因此需要用一个掩模来指出这些部分。要处理缺少的测量,弱分类器必须包含替代的方法(参见CvDTreeParams::use_surrogates)。
- weak_reponses
- 可选的输出参数,weak_reponses是一个浮点数向量,向量中每一个浮点数都对应一个独立弱分类器的响应。向量中元素的数量必须与弱分类器的数量相等。
- slice
- 弱分类器响应中用于预测的连续子集。默认情况下使用所有的弱分类器。
- raw_mode
- 与在CvDTree::predict中的意思相同。一般而言被设为false。
CvBoost::predict方法通过总体的树运行样本,返回输出的加权类标签。
CvBoost::prune
移除指定的弱分类器
void CvBoost::prune( CvSlice slice );
这个方法从结果中移除指定的弱分类器。请注意不要将这个方法与一个目前还不支持的移除单独决策树的方法混淆起来。
CvBoost::get_weak_predictors
返回弱分类树的结果
CvSeq* CvBoost::get_weak_predictors();
这个方法返回弱分类器的结果。每个元素的结果都是一个指向CvBoostTree类的指针(或者也可能指向它的一些派生)。
Random Trees
Random trees have been introduced by Leo Breiman and Adele Cutler: http://www.stat.berkeley.edu/users/breiman/RandomForests/. The algorithm can deal with both classification and regression problems. Random trees is a collection (ensemble) of tree predictors that is called forest further in this section (the term has been also introduced by L. Brieman). The classification works as following: the random trees classifier takes the input feature vector, classifies it with every tree in the forest, and outputs the class label that has got the majority of "votes". In case of regression the classifier response is the average of responses over all the trees in the forest.
All the trees are trained with the same parameters, but on the different training sets, which are generated from the original training set using bootstrap procedure: for each training set we randomly select the same number of vectors as in the original set (=N). The vectors are chosen with replacement. That is, some vectors will occur more than once and some will be absent. At each node of each tree trained not all the variables are used to find the best split, rather than a random subset of them. The each node a new subset is generated, however its size is fixed for all the nodes and all the trees. It is a training parameter, set to sqrt(
In random trees there is no need in any accuracy estimation procedures, such as cross-validation or bootstrap, or a separate test set to get an estimate of the training error. The error is estimated internally during the training. When the training set for the current tree is drawn by sampling with replacement, some vectors are left out (so-called oob (out-of-bag) data). The size of oob data is about N/3. The classification error is estimated by using this oob-data as following:
Get a prediction for each vector, which is oob relatively to the i-th tree, using the very i-th tree. After all the trees have been trained, for each vector that has ever been oob, find the class-"winner" for it (i.e. the class that has got the majority of votes in the trees, where the vector was oob) and compare it to the ground-truth response. Then the classification error estimate is computed as ratio of number of missclassified oob vectors to all the vectors in the original data. In the case of regression the oob-error is computed as the squared error for oob vectors difference divided by the total number of vectors.
References:
Machine Learning, Wald I, July 2002 Looking Inside the Black Box, Wald II, July 2002 Software for the Masses, Wald III, July 2002 And other articles from the web-sitehttp://www.stat.berkeley.edu/users/breiman/RandomForests/cc_home.htm.
CvRTParams Training Parameters of Random Trees
struct CvRTParams : public CvDTreeParams {
bool calc_var_importance; int nactive_vars; CvTermCriteria term_crit;
CvRTParams() : CvDTreeParams( 5, 10, 0, false, 10, 0, false, false, 0 ),
calc_var_importance(false), nactive_vars(0)
{
term_crit = cvTermCriteria( CV_TERMCRIT_ITER+CV_TERMCRIT_EPS, 50, 0.1 );
}
CvRTParams( int _max_depth, int _min_sample_count,
float _regression_accuracy, bool _use_surrogates,
int _max_categories, const float* _priors,
bool _calc_var_importance,
int _nactive_vars, int max_tree_count,
float forest_accuracy, int termcrit_type );
};
calc_var_importance If it is set, then variable importance is computed by the training procedure. To retrieve the computed variable importance array, call the method CvRTrees::get_var_importance(). nactive_vars The number of variables that are randomly selected at each tree node and that are used to find the best split(s). term_crit Termination criteria for growing the forest: term_crit.max_iter is the maximum number of trees in the forest (see also max_tree_count parameter of the constructor, by default it is set to 50) term_crit.epsilon is the sufficient accuracy (OOB error). The set of training parameters for the forest is the superset of the training parameters for a single tree. However, Random trees do not need all the functionality/features of decision trees, most noticeably, the trees are not pruned, so the cross-validation parameters are not used.
CvRTrees Random Trees
class CvRTrees : public CvStatModel { public:
CvRTrees();
virtual ~CvRTrees();
virtual bool train( const CvMat* _train_data, int _tflag,
const CvMat* _responses, const CvMat* _var_idx=0,
const CvMat* _sample_idx=0, const CvMat* _var_type=0,
const CvMat* _missing_mask=0,
CvRTParams params=CvRTParams() );
virtual float predict( const CvMat* sample, const CvMat* missing = 0 ) const;
virtual void clear();
virtual const CvMat* get_var_importance(); virtual float get_proximity( const CvMat* sample_1, const CvMat* sample_2 ) const;
virtual void read( CvFileStorage* fs, CvFileNode* node ); virtual void write( CvFileStorage* fs, const char* name );
CvMat* get_active_var_mask(); CvRNG* get_rng();
int get_tree_count() const; CvForestTree* get_tree(int i) const;
protected:
bool grow_forest( const CvTermCriteria term_crit );
// array of the trees of the forest CvForestTree** trees; CvDTreeTrainData* data; int ntrees; int nclasses; ...
};
CvRTrees::train Trains Random Trees model
bool CvRTrees::train( const CvMat* train_data, int tflag,
const CvMat* responses, const CvMat* comp_idx=0,
const CvMat* sample_idx=0, const CvMat* var_type=0,
const CvMat* missing_mask=0,
CvRTParams params=CvRTParams() );
The method CvRTrees::train is very similar to the first form of CvDTree::train() and follows the generic method CvStatModel::train conventions. All the specific to the algorithm training parameters are passed as CvRTParams instance. The estimate of the training error (oob-error) is stored in the protected class member oob_error.
CvRTrees::predict Predicts the output for the input sample
double CvRTrees::predict( const CvMat* sample, const CvMat* missing=0 ) const; The input parameters of the prediction method are the same as in CvDTree::predict, but the return value type is different. This method returns the cummulative result from all the trees in the forest (the class that receives the majority of voices, or the mean of the regression function estimates).
CvRTrees::get_var_importance Retrieves the variable importance array
const CvMat* CvRTrees::get_var_importance() const; The method returns the variable importance vector, computed at the training stage when CvRTParams::calc_var_importance is set. If the training flag is not set, then the NULL pointer is returned. This is unlike decision trees, where variable importance can be computed anytime after the training.
CvRTrees::get_proximity Retrieves proximitity measure between two training samples
float CvRTrees::get_proximity( const CvMat* sample_1, const CvMat* sample_2 ) const; The method returns proximity measure between any two samples (the ratio of the those trees in the ensemble, in which the samples fall into the same leaf node, to the total number of the trees).
Example. Prediction of mushroom edibility using random trees classifier
- include
- include
- include
- include "ml.h"
int main( void ) {
CvStatModel* cls = NULL; CvFileStorage* storage = cvOpenFileStorage( "Mushroom.xml", NULL,CV_STORAGE_READ ); CvMat* data = (CvMat*)cvReadByName(storage, NULL, "sample", 0 ); CvMat train_data, test_data; CvMat response; CvMat* missed = NULL; CvMat* comp_idx = NULL; CvMat* sample_idx = NULL; CvMat* type_mask = NULL; int resp_col = 0; int i,j; CvRTreesParams params; CvTreeClassifierTrainParams cart_params; const int ntrain_samples = 1000; const int ntest_samples = 1000; const int nvars = 23;
if(data == NULL || data->cols != nvars)
{
puts("Error in source data");
return -1;
}
cvGetSubRect( data, &train_data, cvRect(0, 0, nvars, ntrain_samples) );
cvGetSubRect( data, &test_data, cvRect(0, ntrain_samples, nvars,
ntrain_samples + ntest_samples) );
resp_col = 0; cvGetCol( &train_data, &response, resp_col);
/* create missed variable matrix */
missed = cvCreateMat(train_data.rows, train_data.cols, CV_8UC1);
for( i = 0; i < train_data.rows; i++ )
for( j = 0; j < train_data.cols; j++ )
CV_MAT_ELEM(*missed,uchar,i,j) = (uchar)(CV_MAT_ELEM(train_data,float,i,j) < 0);
/* create comp_idx vector */
comp_idx = cvCreateMat(1, train_data.cols-1, CV_32SC1);
for( i = 0; i < train_data.cols; i++ )
{
if(iresp_col)CV_MAT_ELEM(*comp_idx,int,0,i-1) = i;
}
/* create sample_idx vector */
sample_idx = cvCreateMat(1, train_data.rows, CV_32SC1);
for( j = i = 0; i < train_data.rows; i++ )
{
if(CV_MAT_ELEM(response,float,i,0) < 0) continue;
CV_MAT_ELEM(*sample_idx,int,0,j) = i;
j++;
}
sample_idx->cols = j;
/* create type mask */ type_mask = cvCreateMat(1, train_data.cols+1, CV_8UC1); cvSet( type_mask, cvRealScalar(CV_VAR_CATEGORICAL), 0);
// initialize training parameters cvSetDefaultParamTreeClassifier((CvStatModelParams*)&cart_params); cart_params.wrong_feature_as_unknown = 1; params.tree_params = &cart_params; params.term_crit.max_iter = 50; params.term_crit.epsilon = 0.1; params.term_crit.type = CV_TERMCRIT_ITER|CV_TERMCRIT_EPS;
puts("Random forest results");
cls = cvCreateRTreesClassifier( &train_data, CV_ROW_SAMPLE, &response,
(CvStatModelParams*)& params, comp_idx, sample_idx, type_mask, missed );
if( cls )
{
CvMat sample = cvMat( 1, nvars, CV_32FC1, test_data.data.fl );
CvMat test_resp;
int wrong = 0, total = 0;
cvGetCol( &test_data, &test_resp, resp_col);
for( i = 0; i < ntest_samples; i++, sample.data.fl += nvars )
{
if( CV_MAT_ELEM(test_resp,float,i,0) >= 0 )
{
float resp = cls->predict( cls, &sample, NULL );
wrong += (fabs(resp-response.data.fl[i]) > 1e-3 ) ? 1 : 0;
total++;
}
}
printf( "Test set error = %.2f\n", wrong*100.f/(float)total );
}
else
puts("Error forest creation");
cvReleaseMat(&missed); cvReleaseMat(&sample_idx); cvReleaseMat(&comp_idx); cvReleaseMat(&type_mask); cvReleaseMat(&data); cvReleaseStatModel(&cls); cvReleaseFileStorage(&storage); return 0;
}
Expectation-Maximization
The EM (Expectation-Maximization) algorithm estimates the parameters of the multivariate probability density function in a form of the Gaussian mixture distribution with a specified number of mixtures.
Consider the set of the feature vectors {x1, x2,..., xN}: N vectors from d-dimensional Euclidean space drawn from a Gaussian mixture:
where m is the number of mixtures, pk is the normal distribution density with the mean ak and covariance matrix Sk, πk is the weight of k-th mixture. Given the number of mixtures m and the samples {xi, i=1..N} the algorithm finds the maximum-likelihood estimates (MLE) of the all the mixture parameters, i.e. ak, Sk and πk:
EM algorithm is an iterative procedure. Each iteration of it includes two steps. At the first step (Expectation-step, or E-step), we find a probability pi,k (denoted αi,k in the formula below) of sample #i to belong to mixture #k using the currently available mixture parameter estimates:
At the second step (Maximization-step, or M-step) the mixture parameter estimates are refined using the computed probabilities:
Alternatively, the algorithm may start with M-step when initial values for pi,k can be provided. Another alternative, when pi,k are unknown, is to use a simpler clustering algorithm to pre-cluster the input samples and thus obtain initial pi,k. Often (and in ML) k-means algorithm is used for that purpose. One of the main that EM algorithm should deal with is the large number of parameters to estimate. The majority of the parameters sits in covariation matrices, which are d×d elements each (where d is the feature space dimensionality). However, in many practical problems the covariation matrices are close to diagonal, or even to μk*I, where I is identity matrix and μk is mixture-dependent "scale" parameter. So a robust computation scheme could be to start with the harder constraints on the covariation matrices and then use the estimated parameters as an input for a less constrained optimization problem (often a diagonal covariation matrix is already a good enough approximation).
References:
[Bilmes98] J. A. Bilmes. A Gentle Tutorial of the EM Algorithm and its Application to Parameter Estimation for Gaussian Mixture and Hidden Markov Models. Technical Report TR-97-021, International Computer Science Institute and Computer Science Division, University of California at Berkeley, April 1998.
CvEMParams
EM算法估计混合高斯模型所需要的参数
Parameters of EM algorithm
struct CvEMParams {
CvEMParams() : nclusters(10), cov_mat_type(CvEM::COV_MAT_DIAGONAL),
start_step(CvEM::START_AUTO_STEP), probs(0), weights(0), means(0), covs(0)
{
term_crit=cvTermCriteria( CV_TERMCRIT_ITER+CV_TERMCRIT_EPS, 100, FLT_EPSILON );
}
CvEMParams( int _nclusters, int _cov_mat_type=1/*CvEM::COV_MAT_DIAGONAL*/,
int _start_step=0/*CvEM::START_AUTO_STEP*/,
CvTermCriteria _term_crit=cvTermCriteria(CV_TERMCRIT_ITER+CV_TERMCRIT_EPS, 100, FLT_EPSILON),
CvMat* _probs=0, CvMat* _weights=0, CvMat* _means=0, CvMat** _covs=0 ) :
nclusters(_nclusters), cov_mat_type(_cov_mat_type), start_step(_start_step),
probs(_probs), weights(_weights), means(_means), covs(_covs), term_crit(_term_crit)
{}
int nclusters; int cov_mat_type; int start_step; const CvMat* probs; const CvMat* weights; const CvMat* means; const CvMat** covs; CvTermCriteria term_crit;
};
nclusters
高斯成分的个数,必须事先指定。有些EM的算法可以在给定区间内,自动确定最优个数,不过本算法未实现此功能。
The number of mixtures. Some of EM implementation could determine the optimal number of mixtures within a specified value range, but that is not the case in ML yet.
cov_mat_type
协变矩阵的类型,只能为下面三种类型之一
The type of the mixture covariation matrices; should be one of the following:
对称矩阵 每一个混合的协变矩阵都是任意的对称正定矩阵,因此每个矩阵的自由参数为d2/2。通常来说,除非对参数有非常精确的估计,或者有足够大量的样本,否则不建议使用这个选项。
CvEM::COV_MAT_GENERIC - a covariation matrix of each mixture may be arbitrary symmetrical positively defined matrix, so the number of free parameters in each matrix is about d2/2. It is not recommended to use this option, unless there is pretty accurate initial estimation of the parameters and/or a huge number of training samples.
对角阵(假设数据各维之间是独立的,最常用的情况) 每一个混合的协变矩阵都是任意的正对角阵,也就是说,非对角位置的值必须是0,因此每一个矩阵的自由参数为d。这是一个最常用的选项,也能得到很好的结果。
CvEM::COV_MAT_DIAGONAL - a covariation matrix of each mixture may be arbitrary diagonal matrix with positive diagonal elements, that is, non-diagonal elements are forced to be 0's, so the number of free parameters is d for each matrix. This is most commonly used option yielding good estimation results.
球矩阵 每一个混合的协变矩阵都是全N阵,即μk*I,一次唯一的参数就是μk。这个选项通常用在一些特殊的场合,比如约束条件是相关的,或者作为某些优化算法的第一步(比如,用PCA来预处理数据时)。这个预估计的结果会被再次传递到优化过程中,比如cov_mat_type=CvEM::COV_MAT_DIAGONAL。
CvEM::COV_MAT_SPHERICAL - a covariation matrix of each mixture is a scaled identity matrix, μk*I, so the only parameter to be estimated is μk. The option may be used in special cases, when the constraint is relevant, or as a first step in the optimization (e.g. in case when the data is preprocessed with PCA). The results of such preliminary estimation may be passed again to the optimization procedure, this time with cov_mat_type=CvEM::COV_MAT_DIAGONAL.
start_step
开始步骤, 3种选择
The initial step the algorithm starts from; should be one of the following:
CvEM::START_E_STEP - the algorithm starts with E-step. At least, the initial values of mean vectors, CvEMParams::means must be passed. Optionally, the user may also provide initial values for weights (CvEMParams::weights) and/or covariation matrices (CvEMParams::covs).
CvEM::START_M_STEP - the algorithm starts with M-step. The initial probabilities pi,k must be provided.
CvEM::START_AUTO_STEP - No values are required from the user, k-means algorithm is used to estimate initial mixtures parameters.
term_crit
E步和M步 迭代停止的准则。 EM算法会在一定的迭代次数之后(term_crit.num_iter),或者当模型参数在两次迭代之间的变化小于预定值(term_crit.epsilon)时停止
Termination criteria of the procedure. EM algorithm stops either after a certain number of iterations (term_crit.num_iter), or when the parameters change too little (no more than term_crit.epsilon) from iteration to iteration.
probs
初始的后验概率 Initial probabilities pi,k; are used (and must be not NULL) only when start_step=CvEM::START_M_STEP.
weights
初始的各个成分的概率 Initial mixture weights πk; are used (if not NULL) only when start_step=CvEM::START_E_STEP.
covs
初始的协方差矩阵 Initial mixture covariation matrices Sk; are used (if not NULL) only when start_step=CvEM::START_E_STEP.
means
初始的均值 Initial mixture means ak; are used (and must be not NULL) only when start_step=CvEM::START_E_STEP.
The structure has 2 constructors, the default one represents a rough rule-of-thumb, with another one it is possible to override a variety of parameters, from a single number of mixtures (the only essential problem-dependent parameter), to the initial values for the mixture parameters.
CvEM EM model
class CV_EXPORTS CvEM : public CvStatModel { public:
// Type of covariation matrices
enum { COV_MAT_SPHERICAL=0, COV_MAT_DIAGONAL=1, COV_MAT_GENERIC=2 };
// The initial step
enum { START_E_STEP=1, START_M_STEP=2, START_AUTO_STEP=0 };
CvEM();
CvEM( const CvMat* samples, const CvMat* sample_idx=0,
CvEMParams params=CvEMParams(), CvMat* labels=0 );
virtual ~CvEM();
virtual bool train( const CvMat* samples, const CvMat* sample_idx=0,
CvEMParams params=CvEMParams(), CvMat* labels=0 );
virtual float predict( const CvMat* sample, CvMat* probs ) const; virtual void clear();
int get_nclusters() const { return params.nclusters; }
const CvMat* get_means() const { return means; }
const CvMat** get_covs() const { return covs; }
const CvMat* get_weights() const { return weights; }
const CvMat* get_probs() const { return probs; }
protected:
virtual void set_params( const CvEMParams& params,
const CvVectors& train_data );
virtual void init_em( const CvVectors& train_data );
virtual double run_em( const CvVectors& train_data );
virtual void init_auto( const CvVectors& samples );
virtual void kmeans( const CvVectors& train_data, int nclusters,
CvMat* labels, CvTermCriteria criteria,
const CvMat* means );
CvEMParams params;
double log_likelihood;
CvMat* means; CvMat** covs; CvMat* weights; CvMat* probs;
CvMat* log_weight_div_det; CvMat* inv_eigen_values; CvMat** cov_rotate_mats;
};
CvEM::train Estimates Gaussian mixture parameters from the sample set
void CvEM::train( const CvMat* samples, const CvMat* sample_idx=0,
CvEMParams params=CvEMParams(), CvMat* labels=0 );
Unlike many of ML models, EM is an unsupervised learning algorithm and it does not take responses (class labels or the function values) on input. Instead, it computes MLE of Gaussian mixture parameters from the input sample set, stores all the parameters inside the stucture: pi,k in probs, ak in means Sk in covs[k], πk in weights and optionally computes the output "class label" for each sample: labelsi=arg maxk(pi,k), i=1..N (i.e. indices of the most-probable mixture for each sample).
The trained model can be used further for prediction, just like any other classifier. The model trained is similar to the normal bayes classifier.
Example. Clustering random samples of multi-gaussian distribution using EM
- include "ml.h"
- include "highgui.h"
int main( int argc, char** argv ) {
const int N = 4;
const int N1 = (int)sqrt((double)N);
const CvScalar colors[] = {{{0,0,255}},Template:0,255,0,Template:0,255,255,Template:255,255,0};
int i, j;
int nsamples = 100;
CvRNG rng_state = cvRNG(-1);
CvMat* samples = cvCreateMat( nsamples, 2, CV_32FC1 );
CvMat* labels = cvCreateMat( nsamples, 1, CV_32SC1 );
IplImage* img = cvCreateImage( cvSize( 500, 500 ), 8, 3 );
float _sample[2];
CvMat sample = cvMat( 1, 2, CV_32FC1, _sample );
CvEM em_model;
CvEMParams params;
CvMat samples_part;
cvReshape( samples, samples, 2, 0 );
for( i = 0; i < N; i++ )
{
CvScalar mean, sigma;
// form the training samples
cvGetRows( samples, &samples_part, i*nsamples/N, (i+1)*nsamples/N );
mean = cvScalar(((i%N1)+1.)*img->width/(N1+1), ((i/N1)+1.)*img->height/(N1+1));
sigma = cvScalar(30,30);
cvRandArr( &rng_state, &samples_part, CV_RAND_NORMAL, mean, sigma );
}
cvReshape( samples, samples, 1, 0 );
// initialize model's parameters params.covs = NULL; params.means = NULL; params.weights = NULL; params.probs = NULL; params.nclusters = N; params.cov_mat_type = CvEM::COV_MAT_SPHERICAL; params.start_step = CvEM::START_AUTO_STEP; params.term_crit.max_iter = 10; params.term_crit.epsilon = 0.1; params.term_crit.type = CV_TERMCRIT_ITER|CV_TERMCRIT_EPS;
// cluster the data em_model.train( samples, 0, params, labels );
- if 0
// the piece of code shows how to repeatedly optimize the model // with less-constrained parameters (COV_MAT_DIAGONAL instead of COV_MAT_SPHERICAL) // when the output of the first stage is used as input for the second. CvEM em_model2; params.cov_mat_type = CvEM::COV_MAT_DIAGONAL; params.start_step = CvEM::START_E_STEP; params.means = em_model.get_means(); params.covs = (const CvMat**)em_model.get_covs(); params.weights = em_model.get_weights();
em_model2.train( samples, 0, params, labels ); // to use em_model2, replace em_model.predict() with em_model2.predict() below
- endif
// classify every image pixel
cvZero( img );
for( i = 0; i < img->height; i++ )
{
for( j = 0; j < img->width; j++ )
{
CvPoint pt = cvPoint(j, i);
sample.data.fl[0] = (float)j;
sample.data.fl[1] = (float)i;
int response = cvRound(em_model.predict( &sample, NULL ));
CvScalar c = colors[response];
cvCircle( img, pt, 1, cvScalar(c.val[0]*0.75,c.val[1]*0.75,c.val[2]*0.75), CV_FILLED );
}
}
//draw the clustered samples
for( i = 0; i < nsamples; i++ )
{
CvPoint pt;
pt.x = cvRound(samples->data.fl[i*2]);
pt.y = cvRound(samples->data.fl[i*2+1]);
cvCircle( img, pt, 1, colors[labels->data.i[i]], CV_FILLED );
}
cvNamedWindow( "EM-clustering result", 1 ); cvShowImage( "EM-clustering result", img ); cvWaitKey(0);
cvReleaseMat( &samples ); cvReleaseMat( &labels ); return 0;
}
神经网络
ML implements feedforward artificial neural networks, more particularly, multi-layer perceptrons (MLP), the most commonly used type of neural networks. MLP consists of the input layer, output layer and one or more hidden layers. Each layer of MLP includes one or more neurons that are directionally linked with the neurons from the previous and the next layer. Here is an example of 3-layer perceptron with 3 inputs, 2 outputs and the hidden layer including 5 neurons:
ML实现了前馈(feedforward)人工神经元网络(ANN),准确地说是最常用的神经元网络,multi-layerperceptrons (MLP)。MLP由输入层、输出层和一个或多个隐藏层构成。MLP的每一层包含了一个或多个神经元,它们从之前的层和之后的层的神经元有向的连接在一起。下面是一个三层感知器(perceptron)的例子,其由3个输入、2个输出以及包含5个神经元的隐藏层构成:
All the neurons in MLP are similar. Each of them has several input links (i.e. it takes the output values from several neurons in the previous layer on input) and several output links (i.e. it passes the response to several neurons in the next layer). The values retrieved from the previous layer are summed with certain weights, individual for each neuron, plus the bias term, and the sum is transformed using the activation function f that may be also different for different neurons. Here is the picture:
MLP中所有的神经元都是相似的。每一个有多个输入链路(比如,取前一层的多个神经元的输出作为自己的输入)和多个输出链路(比如传递响应到下一层的多个神经元)。
In other words, given the outputs {xj} of the layer n, the outputs {yi} of the layer n+1 are computed as:
ui=sumj(w(n+1)i,j*xj) + w(n+1)i,bias yi=f(ui)
Different activation functions may be used, the ML implements 3 standard ones:
Identity function (CvANN_MLP::IDENTITY): f(x)=x Symmetrical sigmoid (CvANN_MLP::SIGMOID_SYM): f(x)=β*(1-e-αx)/(1+e-αx), the default choice for MLP; the standard sigmoid with β=1, α=1 is shown below: Gaussian function (CvANN_MLP::GAUSSIAN): f(x)=βe-αx*x, not completely supported by the moment. In ML all the neurons have the same activation functions, with the same free parameters (α, β) that are specified by user and are not altered by the training algorithms.
ML实现了三种标准激活函数(神经元的传递函数): 恒等函数:f(x)=x,CvANN_MLP::IDENTITY。 对称S函数:f(x)= β*(1-e-αx)/(1+e-αx),该函数是默认激活函数,贝塔=1,阿尔法=1的标准的S函数如下所示;CvANN_MLP::SIGMOID_SYM。 高斯函数: f(x)=βe-αx*x,目前未被完全支持(哪个opencv版本??);CvANN_MLP::GAUSSIAN。ML中,所有神经元有相同的激活函数,有相同的自由参数(α,β),(α,β)由用户指定,且不会被训练算法改变。
So the whole trained network works as following. It takes the feature vector on input, the vector size is equal to the size of the input layer, when the values are passed as input to the first hidden layer, the outputs of the hidden layer are computed using the weights and the activation functions and passed further downstream, until we compute the output layer.
训练后的网络工作过程如下:从输入节点接收特征向量,特征向量大小与输入层相同,特征向量的值作为输入传递到第一个隐层,隐层的输出用权值和激活函数计算,然后传递到下一层, 直至计算完输出层。
So, in order to compute the network one need to know all the weights w(n+1)i,j. The weights are computed by the training algorithm. The algorithm takes a training set: multiple input vectors with the corresponding output vectors, and iteratively adjusts the weights to try to make the network give the desired response on the provided input vectors.
可见,要计算网络,就需要知道所有的权值w(n+1)i,j。权值由训练算法计算。训练算法有一个训练集:即多输入向量和对应的输出向量,算法迭代的调整权值,目标是对给定输入向量,网络能输出其对应的期望响应。
The larger the network size (the number of hidden layers and their sizes), the more is the potential network flexibility, and the error on the training set could be made arbitrarily small. But at the same time the learned network will also "learn" the noise present in the training set, so the error on the test set usually starts increasing after the network size reaches some limit. Besides, the larger networks are train much longer than the smaller ones, so it is reasonable to preprocess the data (using PCA or similar technique) and train a smaller network on only the essential features.
网络规模(隐层数和隐层节点数)越大,潜在的网络适应性越强,训练集的误差就可能降到任意小;但是同时,学习后的网络也会学习训练集里的噪声部分,因此,测试集的误差通常会在网络规模增加到一定程度后增大;此外,网络规模越大,训练时间越长。因此,有必要对数据进行预处理(用PCA或类似技术),并且应该用必要的特征训练一个较小的网络。
Another feature of the MLP's is their inability to handle categorical data as is, however there is a workaround. If a certain feature in the input or output (i.e. in case of n-class classifier for n>2) layer is categorical and can take M (>2) different values, it makes sense to represent it as binary tuple of M elements, where i-th element is 1 if and only if the feature is equal to the i-th value out of M possible. It will increase the size of the input/output layer, but will speedup the training algorithm convergence and at the same time enable "fuzzy" values of such variables, i.e. a tuple of probabilities instead of a fixed value.
MLP的另一个特征是,对处理分类数据无能为力,虽然有相关的工作(???)。如果输入或输出层(例如,n-class分类器,n>2)的某特征是分类的,且可取M(>2)个不同的值,那么将其表示为M个元素的二元组是有意义的,即:当且仅当该特征符合那M个可能值中的第i时,二元组的第i个元素是1。这会增加输入输出层的规模,但是将会加快训练算法收敛,同时使能此类变量的模糊值,例如,一组概率而不是一组固定值。
ML implements 2 algorithms for training MLP's. The first is the classical random sequential backpropagation algorithm and the second (default one) is batch RPROP algorithm
ML实现了两种训练MLP的算法:经典随即序列反向传播算法,和batch RPROP算法(默认)。
References:
http://en.wikipedia.org/wiki/Backpropagation. Wikipedia article about the backpropagation algorithm. Y. LeCun, L. Bottou, G.B. Orr and K.-R. Muller, "Efficient backprop", in Neural Networks---Tricks of the Trade, Springer Lecture Notes in Computer Sciences 1524, pp.5-50, 1998. M. Riedmiller and H. Braun, "A Direct Adaptive Method for Faster Backpropagation Learning: The RPROP Algorithm", Proc. ICNN, San Fransisco (1993).
CvANN_MLP_TrainParams Parameters of MLP training algorithm
struct CvANN_MLP_TrainParams {
CvANN_MLP_TrainParams();
CvANN_MLP_TrainParams( CvTermCriteria term_crit, int train_method,
double param1, double param2=0 );
~CvANN_MLP_TrainParams();
enum { BACKPROP=0, RPROP=1 };
CvTermCriteria term_crit; int train_method;
// backpropagation parameters double bp_dw_scale, bp_moment_scale;
// rprop parameters double rp_dw0, rp_dw_plus, rp_dw_minus, rp_dw_min, rp_dw_max;
}; term_crit The termination criteria for the training algorithm. Identifies how many iteration is done by the algorithm (for sequential backpropagation algorithm the number is multiplied by the size of the training set) and how much the weights could change between the iterations to make the algorithm continue. train_method The training algoithm to use; can be one of CvANN_MLP_TrainParams::BACKPROP (sequential backpropagation algorithm) or CvANN_MLP_TrainParams::RPROP (RPROP algorithm, default value). bp_dw_scale (Backpropagation only): The coefficient to multiply the computed weight gradient by. The recommended value is about 0.1. The parameter can be set via param1 of the constructor. bp_moment_scale (Backpropagation only): The coefficient to multiply the difference between weights on the 2 previous iterations. Provides some inertia to smooth the random fluctuations of the weights. Can vary from 0 (the feature is disabled) to 1 and beyond. The value 0.1 or so is good enough. The parameter can be set via param2 of the constructor. rp_dw0 (RPROP only): Initial magnitude of the weight delta. The default value is 0.1. The parameter can be set via param1 of the constructor. rp_dw_plus (RPROP only): The increase factor for the weight delta. Must be >1, default value is 1.2 that should work well in most cases, according to the algorithm author. The parameter can only be changed explicitly by modifying the structure member. rp_dw_minus (RPROP only): The decrease factor for the weight delta. Must be <1, default value is 0.5 that should work well in most cases, according to the algorithm author. The parameter can only be changed explicitly by modifying the structure member. rp_dw_min (RPROP only): The minimum value of the weight delta. Must be >0, the default value is FLT_EPSILON. The parameter can be set via param2 of the constructor. rp_dw_max (RPROP only): The maximum value of the weight delta. Must be >1, the default value is 50. The parameter can only be changed explicitly by modifying the structure member. The structure has default constructor that initalizes parameters for RPROP algorithm. There is also more advanced constructor to customize the parameters and/or choose backpropagation algorithm. Finally, the individial parameters can be adjusted after the structure is created.
term_crit:训练算法的终止标准,确定算法的最大迭代次数(对序列反向传播算法,该值乘以训练集大小)和两次迭代间权值变化量。
Train_method 训练算法,可以是CvANN_MLP_TrainParams::BACKPROP (随机序列反向传播) 或者CvANN_MLP_TrainParams::RPROP (RPROP,默认值)。
bp_dw_scale(只用于bp网络),该系数乘以计算出的权值梯度,推荐值为0.1。该参数可通过构造函数的param1设置。
bp_moment_scale(只用于bp网络),该系数乘以前两次迭代的权值之差,平滑权值的随机影响,取值从0-1(0对应的特征被disable)或更大,0.1左右已经足够了。可通过构造函数的param1设置
rp_dw0 (RPROP only):权值delta的初始化幅值,默认值为0.1,可通过构造函数的param1设置。
rp_dw_plus(RPROP only):权值delta的增长因子,必须大于1,默认为1.2(根据算法的作者,该值大部分情况下可行)。该参数只能通过修改结构体成员来显式更改。
rp_dw_minus (RPROP only): 权值delta的减小因子,必须小于1,默认为0.5(根据算法的作者,该值大部分情况下可行)。该参数只能通过修改结构体成员来显式更改。
rp_dw_min (RPROP only): 权值delta的最小值,必须大于0,默认为FLT_EPSILON,可通过构造函数param2设置
rp_dw_max (RPROP only): 权值delta的最大值,必须大于1,默认为50,该参数只能通过修改结构体成员来显式更改。
结构体带有默认构造函数,初始化RPROP 算法参数。也有更多构造函数可以定制参数、选择bp算法。单个参数可在结构体创建后调整
CvANN_MLP MLP model
class CvANN_MLP : public CvStatModel { public:
CvANN_MLP();
CvANN_MLP( const CvMat* _layer_sizes,
int _activ_func=SIGMOID_SYM,
double _f_param1=0, double _f_param2=0 );
virtual ~CvANN_MLP();
virtual void create( const CvMat* _layer_sizes,
int _activ_func=SIGMOID_SYM,
double _f_param1=0, double _f_param2=0 );
virtual int train( const CvMat* _inputs, const CvMat* _outputs,
const CvMat* _sample_weights, const CvMat* _sample_idx=0,
CvANN_MLP_TrainParams _params = CvANN_MLP_TrainParams(),
int flags=0 );
virtual float predict( const CvMat* _inputs,
CvMat* _outputs ) const;
virtual void clear();
// possible activation functions
enum { IDENTITY = 0, SIGMOID_SYM = 1, GAUSSIAN = 2 };
// available training flags
enum { UPDATE_WEIGHTS = 1, NO_INPUT_SCALE = 2, NO_OUTPUT_SCALE = 4 };
virtual void read( CvFileStorage* fs, CvFileNode* node ); virtual void write( CvFileStorage* storage, const char* name );
int get_layer_count() { return layer_sizes ? layer_sizes->cols : 0; }
const CvMat* get_layer_sizes() { return layer_sizes; }
protected:
virtual bool prepare_to_train( const CvMat* _inputs, const CvMat* _outputs,
const CvMat* _sample_weights, const CvMat* _sample_idx,
CvANN_MLP_TrainParams _params,
CvVectors* _ivecs, CvVectors* _ovecs, double** _sw, int _flags );
// sequential random backpropagation virtual int train_backprop( CvVectors _ivecs, CvVectors _ovecs, const double* _sw );
// RPROP algorithm virtual int train_rprop( CvVectors _ivecs, CvVectors _ovecs, const double* _sw );
virtual void calc_activ_func( CvMat* xf, const double* bias ) const;
virtual void calc_activ_func_deriv( CvMat* xf, CvMat* deriv, const double* bias ) const;
virtual void set_activ_func( int _activ_func=SIGMOID_SYM,
double _f_param1=0, double _f_param2=0 );
virtual void init_weights();
virtual void scale_input( const CvMat* _src, CvMat* _dst ) const;
virtual void scale_output( const CvMat* _src, CvMat* _dst ) const;
virtual void calc_input_scale( const CvVectors* vecs, int flags );
virtual void calc_output_scale( const CvVectors* vecs, int flags );
virtual void write_params( CvFileStorage* fs ); virtual void read_params( CvFileStorage* fs, CvFileNode* node );
CvMat* layer_sizes; CvMat* wbuf; CvMat* sample_weights; double** weights; double f_param1, f_param2; double min_val, max_val, min_val1, max_val1; int activ_func; int max_count, max_buf_sz; CvANN_MLP_TrainParams params; CvRNG rng;
}; Unlike many other models in ML that are constructed and trained at once, in MLP these steps are separated. First, a network with the specified topology is created using the non-default constructor or the method create. All the weights are set to zero's. Then the network is trained using the set of input and output vectors. The training procedure can be repeated more than once, i.e. the weights can be adjusted based on the new training data.
与ml中的其他构造和训练一次完成的模式不同,MLP中,这些步骤是分开的。首先,用非默认的构造函数或方法创建指定拓扑的网络,所有的权值设置为0,然后,使用输入输出集训练网络。训练过程可以重复1次以上,例如,权值可在新的训练数据基础上调整。
CvANN_MLP::create Constructs the MLP with the specified topology
void CvANN_MLP::create( const CvMat* _layer_sizes,
int _activ_func=SIGMOID_SYM,
double _f_param1=0, double _f_param2=0 );
_layer_sizes The integer vector, specifying the number of neurons in each layer, including the input and the output ones. _activ_func Specifies the activation function for each neuron; one of CvANN_MLP::IDENTITY, CvANN_MLP::SIGMOID_SYM and CvANN_MLP::GAUSSIAN. _f_param1, _f_param2 Free parameters of the activation function, α and β, respectively. See the formulas in the introduction section.
The method creates MLP network with the specified topology and assigns the same activation function to all the neurons.
_layer_sizes是整数向量,指定每层的神经元数目,包括输入层和输出层。
_activ_func为每个神经元指定激活函数;三种激活函数中的一种
_f_param1 _f_param2 激活函数的自由参数(α and β),参见introductionsection的的论坛
该方法(该函数)创建指定拓扑的MLP网络,给每个神经元确定同样的激活函数。
CvANN_MLP::train Trains/updates MLP
int CvANN_MLP::train( const CvMat* _inputs, const CvMat* _outputs,
const CvMat* _sample_weights, const CvMat* _sample_idx=0,
CvANN_MLP_TrainParams _params = CvANN_MLP_TrainParams(),
int flags=0 );
_inputs A floating-point matrix of input vectors, one vector per row. _outputs A floating-point matrix of the corresponding output vectors, one vector per row. _sample_weights (RPROP only) The optional floating-point vector of weights for each sample. Some samples may be more important than others for training, e.g. user may want to gain the weight of certain classes to find the right balance between hit-rate and false-alarm rate etc. _sample_idx The optional integer vector indicating the samples (i.e. rows of _inputs and _outputs) that are taken into account. _params The training params. See CvANN_MLP_TrainParams description. _flags The various algorithm parameters. May be a combination of the following: UPDATE_WEIGHTS = 1 - update the network weights, rather than compute them from scratch (in the latter case the weights are intialized using Nguyen-Widrow algorithm). NO_INPUT_SCALE - do not normalize the input vectors. If the flag is not set, the training algorithm normalizes each input feature independently, shifting its mean value to 0 and making the standard deviation =1. If the network is assumed to be updated frequently, the new training data should be much different from original one. In this case user should take care of proper normalization. NO_OUTPUT_SCALE - do not normalize the output vectors. If the flag is not set, the training algorithm normalizes each output features independently, by trasforming it to the certain range depending on the activation function used.
_inputs 浮点数输入向量矩阵,每行一个向量。
_outputs 浮点数输出向量矩阵,每行一个向量
_sample_weghts(RPROP only) 可选浮点数矩阵,每个样本的权值向量。某些样本可能比用于训练的其他样本重要。用户可能想增加某些类的权值,以平衡命中率和误判率。
_sample_idx 可选正数向量,表示被考虑的样本(如,_inputs _outputs的行)
_params 训练参数 参见CvANN_MLP_TrainParams的描述
_flags 不同算法的参数 可能是下面的组合:
UPDATE_WEIGHTS = 1 更新网络权值,而不是从scratch计算(此法中,用Nguyen-Widrow算法初始化权值)
NO_INPUT_SCALE 不规格化输入向量。如果标志没有设置,训练算法将每个输入特征单独规格化,将均值变为0,标准差变为1。假定网络频繁更新,新的训练数据会与原始数据差别较些,这种情况下,用户应注意归一化。
NO_OUTPUT_SCALE 不规格化输出向量,如果标志没有设置,训练算法会将每个输出特征独立规格化,根据所用激活函数将其变换到某个范围内。
The method applies the specified training algorithm to compute/adjust the network weights. It returns the number of iterations done.
该方法(该函数)用指定的训练方法计算/调节网络权值,返回迭代次数
中文翻译者
- 于仕琪,中科院自动化所自由软件协会
- 张鲁闽,中科院自动化所自由软件协会
- 王国钦,中科院自动化所自由软件协会
- 姚 谦, 中科院遥感应用研究所