SPSS(七)非线性回归过程
SPSS(七)非线性回归过程
直线关系毕竟是较少数的情形,当因变量和自变量呈曲线关系,我们可以使用回归分析衍生方法----曲线拟合过程
但是使用曲线拟合过程还是存在局限性的
- 只能分析一个自变量
- 变量变换的局限
有的公式根本无法进行变换,如复杂的等式,或者无简单解的积分方程
当变换后,变量的数值分布状况已经改变,此时根据最小二乘法得到的最优解可能在原变量分布状况下并非最优
非线性回归过程
非线性回归过程的优势
- 它采用迭代方法对用户设置的各种复杂曲线模型进行拟合:迭代方法往往意味着结果较为稳定
- 将残差的定义从最小二乘法向外大大扩展,这意味着误差测量手段的大大丰富,我们可以使用最小一乘法、加权最小二乘法、自回归模型等
- 为用户提供了极为强大的分析能力,特别适用于实验室数据的分析
案例:毒物通风数据
这个案例其实在曲线拟合过程已经坐做一次了,这次我们使用非线性回归过程解决
1 2.1250
2 1.7420
3 1.2360
4 1.1270
5 .7310
6 .4690
7 .4000
8 .3810
9 .2840
10 .2760
11 .0620
12 .0610
13 .0408
14 .0428
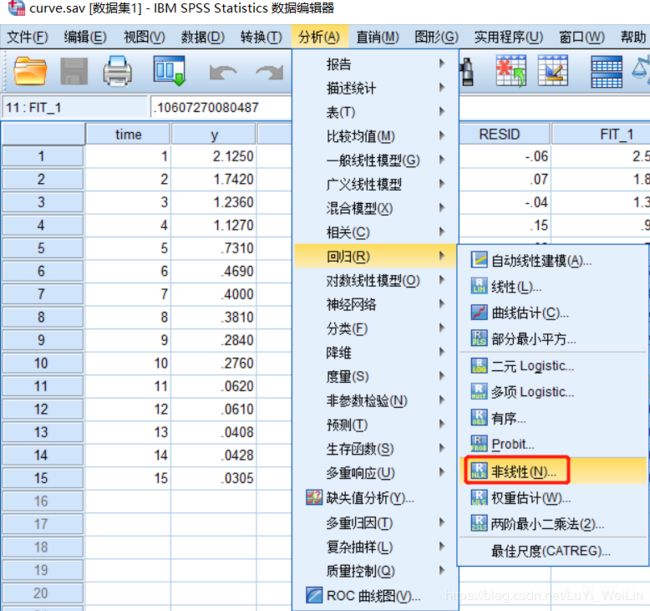
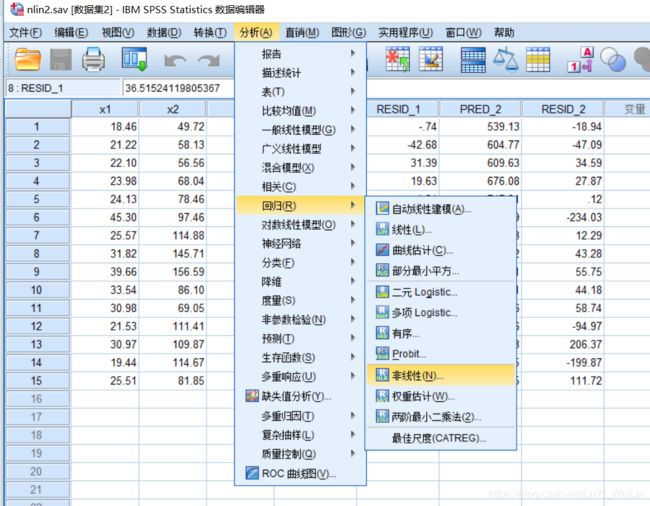
15 .0305分析--回归--非线性
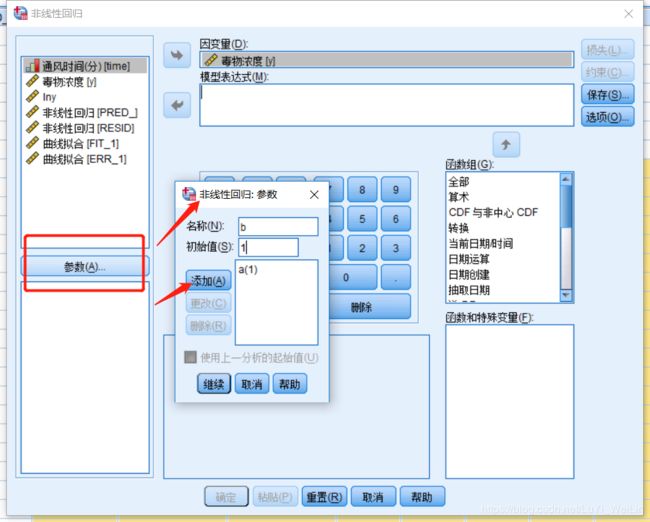
我们假设模型为指数分布(也可以假设为其他分布),设置参数,写模型表达式,操作如下
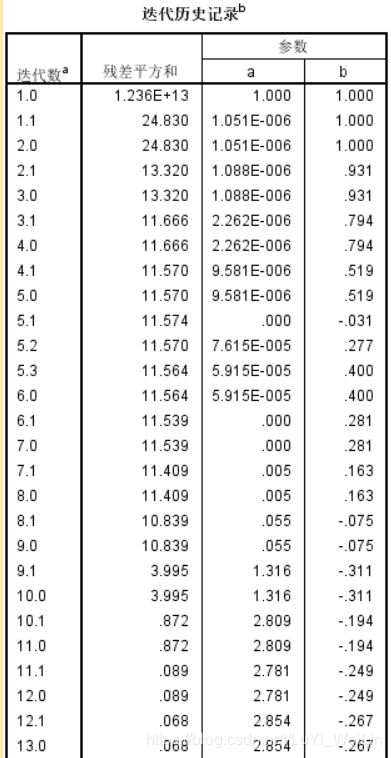
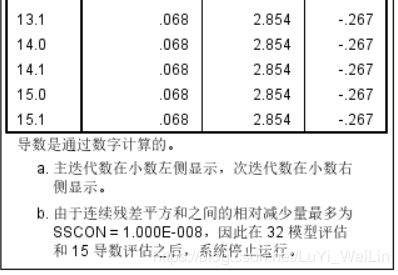
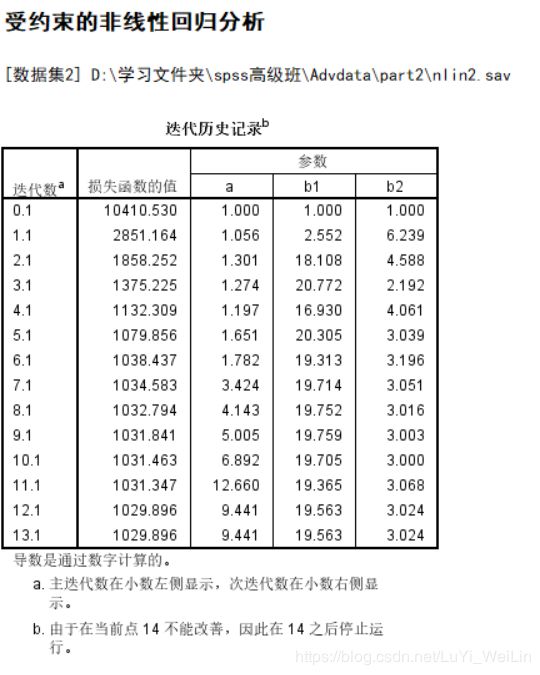
1:从“迭代历史记录”表中可以看出:迭代了30次后,迭代被终止,已经找到最优解
此方法是不断地将“参数估计值”代入”损失函数“求解, 而损失函数采用的是”残差平方和“最小,在迭代30次后,残差平方和达到最小值,最小值为(0.068)此时找到最优解,迭代终止
2:从参数估计值”表中可以看出:
a= 2.854 (标准误为0.101,很小,说明此估计值的置信度很高) b=-0.267(标准误为:0.012,非常小,说明此估计值的置信度高)
非线性模型表达式为:Y(毒物浓度)= 2.854 *e^(-0.267*时间)
3:从“参数估计值的相关性”表中可以看出:变量间的相关性
4:从anova表中可以看出:R方 = 1- (残差平方和)/(已更正的平方和) = 0.989, 拟合度为0.989,说明此模型能够解释98%的变异,拟合度非常高
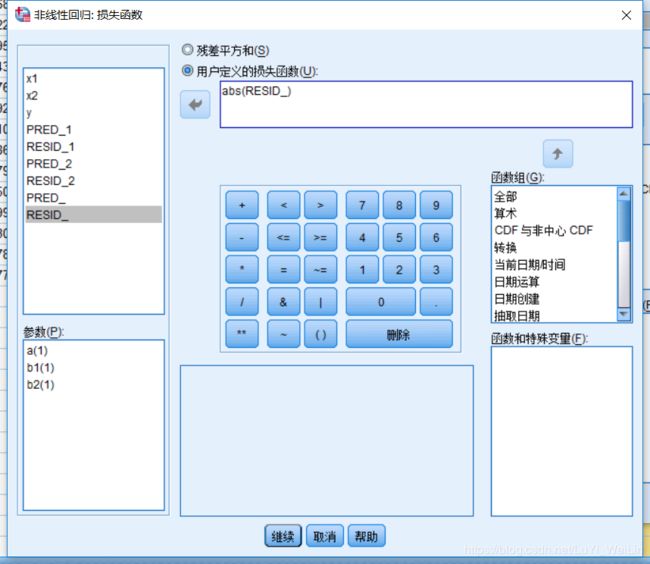
自定义损失函数
针对问题:回归过程有强离群点,而且强离群不好剔除有实际意义
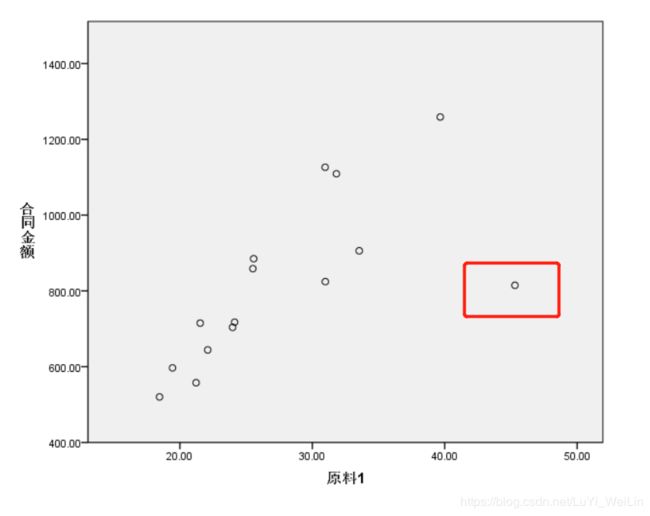
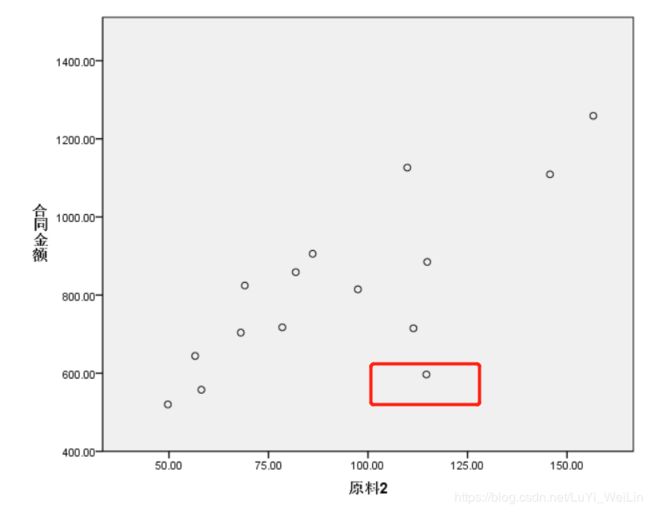
案例:某公司生产的产品其成本主要受两种原材料的影响,为及时调整生产,协调库存,现收集了一批产品产量与相应生产中两种原材料消耗量的数据。请就此建立原材料消耗量与产量(因变量)间的回归方程
数据集如下
18.46 49.72 520.19
21.22 58.13 557.68
22.10 56.56 644.22
23.98 68.04 703.95
24.13 78.46 717.43
45.30 97.46 814.76
25.57 114.88 884.92
31.82 145.71 1109.10
39.66 156.59 1258.86
33.54 86.10 905.79
30.98 69.05 824.50
21.53 111.41 714.99
30.97 109.87 1126.30
19.44 114.67 596.78
25.51 81.85 858.77我们首先观察散点图
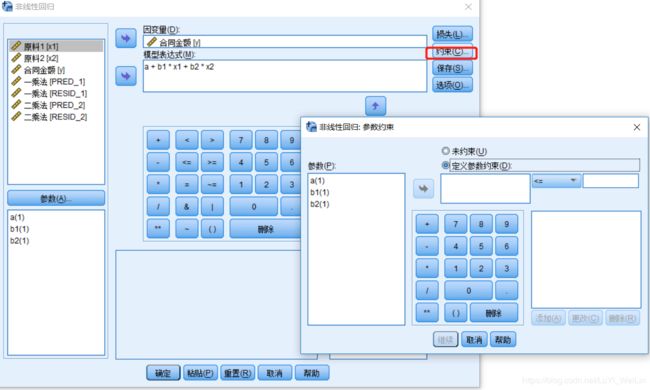
我们选用对强离群点比较耐受的损失函数,最小一乘法,一般线性回归模型都是使用最小二乘法
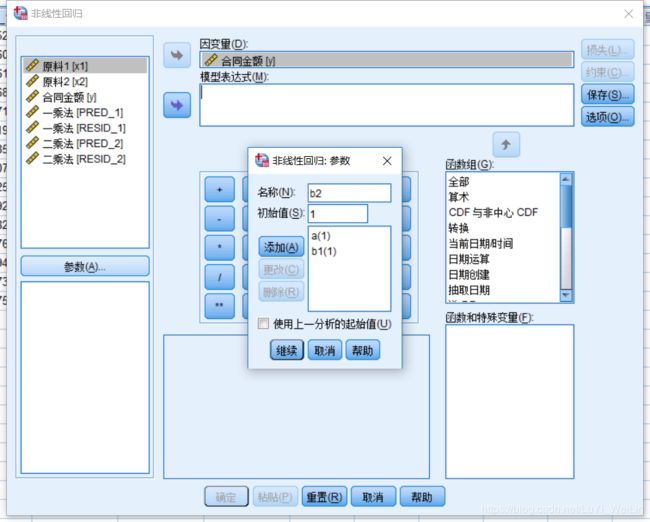
添加参数起始值
定义模型表达式
最小一乘法,残差绝对值之和最小
结果没有检验和标准误差的估计了,只有参数估计值,检验和标准误估计是最小二乘法那一套,对最小一乘法没有意义
参数初始值的设定技巧
- 如果可变为线性,可以先拟合线性方程,将此结果作为初始值
- 如果方程可解,则代入若干样本值,解出近似取值作为初值
- 先拟合较简单的雏形,将结果作为初始值
否则,多尝试几种初始值,观察结果