递归与分治法经典例子
文章目录
- 关于算法
- 递归与分治法基本概念
- 递归经典例子
- hanoi塔
- 分治法经典例子
- 整数排列(全排列问题)
- 整数划分
- 二分搜索
- 大数乘法
- 棋盘覆盖
- 归并排序、快速排序
- 循环赛程表
- 最接近点对
关于算法
问题1:算法基本概念/算法和程序:定义和区别是什么?
概念/定义和区别:
- 算法:指解决问题的方法或过程。
- 程序:是算法用某种程序设计语言的具体实现。
- 程序可以不满足算法性质的有限性。
问题2:算法的复杂性统计/复杂性分析和估算:简单分析与估算。
- 算法复杂性的高低体现在运行该算法所需要的计算机资源的多少,所以有时间复杂性和空间复杂性之分。
- 为简化算法复杂性的分析,引入渐进符号:O(上界)、Ω(下界)、Θ(同阶)、o、ω
递归与分治法基本概念
- 递归:直接或间接地调用自身的算法称为递归算法。
- 分治:大问题分解为小问题,对这k个子问题分别求解。将求出的小规模的问题的解合并为一个更大规模的问题的解,自底向上逐步求出原来问题的解。
递归经典例子
hanoi塔
有三根针a、b、c。a 针上有N个盘子,大的在下,小的在上,要求把这N个盘子从 a 针移到 b 针,在移动过程中可以借助 c 针,每次只允许移动一个盘,且在移动过程中在三根针上都保持大盘在下,小盘在上。
解决思路:
- 当 n=1 时,直接将圆盘从 a 移到 b。
- 当 n>1 时,需要利用 b,将 n-1 个圆盘移到 c 上,然后将剩下的最大圆盘移到 b
- 最后利用 a,将 n-1 个较小的圆盘从 c 移到 b 上(递归子问题 n-1)。
我们将n个圆盘的移动问题就分解成了两次 n-1 个圆盘的移动问题。
递归算法:
public static void hanoi(int n,int a,int b,int c){
if(n==1){
move(a,b);
}else{
hanoi(n-1,a,c,b);
move(a,b);
hanoi(n-1,c,b,a);
}
}
分治法经典例子
整数排列(全排列问题)
解决思路:
依次将待排列的数组的后n-1个元素与第一个元素交换,则每次递归处理的都是后n-1个元素的全排列。当数组元素仅有一个时为此递归算法的出口。
伪代码:
public void Perm(int[] a,int k,int n){
if(k==m){
for(int i=0;i<n;i++){
System.out.println(a[i]);
}
}else{
for(int i=k;i<n;i++){
swap(a,i,k);
perm(a,k+1,m);
swap(a,i,k);
}
}
}
整数划分
问题:将给定正整数n表示成一系列正整数之和
n=n1+n2+…+nk,其中n1≥n2≥…≥nk≥1,k≥1。
求正整数n的不同划分个数p(n)
解决思路:
设 n 是要划分的数,最大加数 ni 不大于 m,用 f(n,m) 表示整数 n 在最大加数为 m 时的划分个数,则可以得到如下递归式。
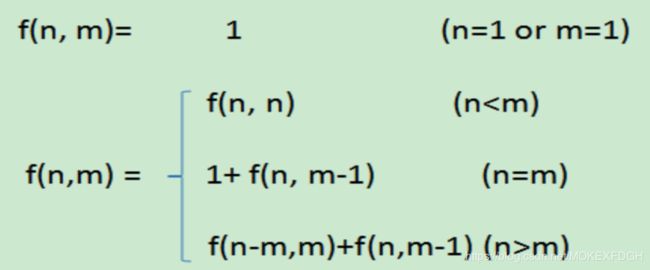
特别注意:f(n,m) = f(n-m,m)+f(n,m-1)
- f(n-m,m):包含 m 的情况,则需要减去要划分的数为n-m,最大数为m
- f(n,m-1):不包含m的情况
伪代码:
public int solution(int n,int m){
if(n==1 || m==1){
return 1;
}
if(n<m){
return solution(n,n)
}
if(n==m){
return 1+solution(n,m-1);
}
if(n>m){
return solution(n-m)+solution(n,m-1);
}
}
二分搜索
问题:给定已排好序的 n 个元素,要在这 n 个元素中找出特定的元素 x。
解决思路:
将 n 个元素分成个数大致相同的两半,将第 n/2 个元素与 x 进行比较,直到找到与 x 相等的元素。
伪代码:
public static int binarySearch(int[] a,int x,int n){
int left = 0;
int right = n-1;
while(left<=right){
int mid = (left+right)/2;
if(x==a[mid])
return mid;
if(x<a[mid])
right = mid-1;
else
left = mid+1;
}
return -1;
}
大数乘法
解决思路:
将 n 位二进制整数 X 和 Y,分成两段:
- X 的前 n/2 位为 A,后 n/2 位为 B,则 X = A2^(n/2) + B
- Y的前 n/2 位位 C,后 n/2 位为 D,则 Y = C2^(n/2) + D
则相乘可以写成 XY = AC2^n + ((A-B)(D-C)+AC+BD)2^(n/2) + BD
分析:
当 n=1 时,T(n) = O(1)
当 n>1 时,3T(n/2)+O(n),由此时间复杂性将为O(n^1.59)
棋盘覆盖

解决思路:
当 k>0 时,将 2^k × 2^k 棋盘分割为 4 个 2^(k-1) × 2^(k-1) 子棋盘,其中一个子棋盘必定会有一个特殊方格,为了其余 3 个子棋盘也有特色放个,可以用一个 L 型的覆盖汇合处:
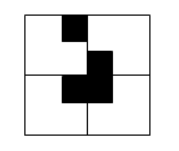
这样就将原问题转化位 4 个较小规模的棋盘覆盖问题,直到棋盘简化为 1 × 1 棋盘。
伪代码:
public void chessBoard(int tr,int tc,int dr,int dc,int size){
//tr,tc:左上角方格的行列号;dr,dc:特殊方格所在行列号;size:棋盘的k
int t=i++;//用来表示第i块L型
int s = size/2;//划分后新的size
if(size==1)
return;
//左上角
if(dr<tr+s && dc<tc+s){//特殊方格在这个子棋盘
chessBoard(tr,tc,dr,dc,s);//递归覆盖其余方格
}else{
board[tr+s-1][tc+s-1] = t;//board表示棋盘,无特殊方格右下角填充L型
chessBoard(tr,tc,tr+s-1,tc+s-1,s);//递归覆盖其余方格
}
//右下角、左下角、右下角同理...
}
分析:
当 k=0 时,T(k) = O(1)
当 k>0 时,4T(K-1) + O(1)
归并排序、快速排序
归并排序思路:
将待排序元素分成大小大致相同的 2 个子集合,分别对 2 个子集合进行排序,最终将排好序的子集合合并成为所要求的排好序的集合。
public static void mergeSort(Comparable[] a){
Comparable[] b = new Comparable[a.length];
int s=1;
while(s<a.length){
mergePass(a,b,s);
s += s;
mergePass(b,a,s);
s += s;
}
}
快速排序思路:
- 将 a[p:r] 分成三段:a[p:q-1]、a[q]、a[q+1:r],使得 a[p:q-1] 中的任何元素都小于等于 a[q],a[q+1,r] 中的任何元素都大于等于 a[q]。
- 分别对 a[p:q-1] 和 a[q+1:r] 进行递归调用快速排序算法,最后得到的 a[p:r] 就是排好序的。
public static void qSort(int p,int r){
if(p<r){
int q = partion(p,r);
qSort(p,q-1);
qSort(q+1,r);
}
}
循环赛程表
问题:有n=2^k个运动员要进行网球循环赛。现要设计一个满足以下要求的比赛日程表:
(1)每个选手必须与其他n-1个选手各赛一次;
(2)每个选手一天只能参赛一次;
(3)循环赛在n-1天内结束。
请按此要求将比赛日程表设计成有n行和n-1列的一个表。在表中的第i行,第j列处填入第i个选手在第j天所遇到的选手。其中1≤i≤n,1≤j≤n-1。
解决思路:
(1)由初始化的第一行填充第二行
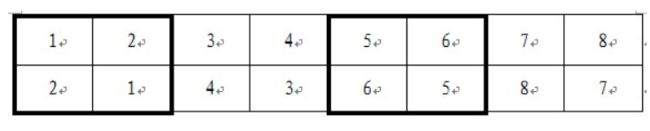
(2)由s控制的第一部分填完。然后是s++,进行第二部分的填充

(3)最后是第三部分的填充

伪代码:
public static table(int k,int[][] a){
int n=1;
for(int i=1;i<=k;i++)
n *= 2;
for(int i=1;i<=n;i++)
a[1][i] = i;
int m = 1;
for(int s=1;s<=k;s++){
n /= 2;
for(int t=1;t<=n;t++){
for(int i=m+1;i<=2*m;i++){
for(int j=m+1;j<=2*m;j++){
a[i][j+(t-1)*m*2] = a[i-m][j+(t-1)*m*2-m];
a[i][j+(t-1)*m*2-m] = a[i-m][j+(t-1)*m*2];
}
}
}
m *= 2;
}
}
最接近点对
问题:定平面上n个点,找其中的一对点,使得在n个点的所有点对中,该点对的距离最小。严格地说,最接近点对可能多于1对。为了简单起见,这里只限于找其中的一对。
解决思路:
首先对集合进行如下的划分:
d = min{d1,d2}
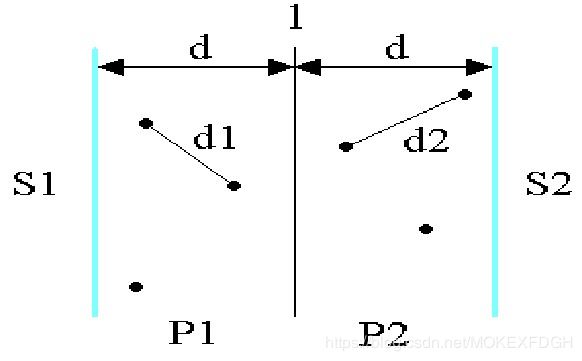
可能存在 p∈P1,q∈P2,且 distance(p,q)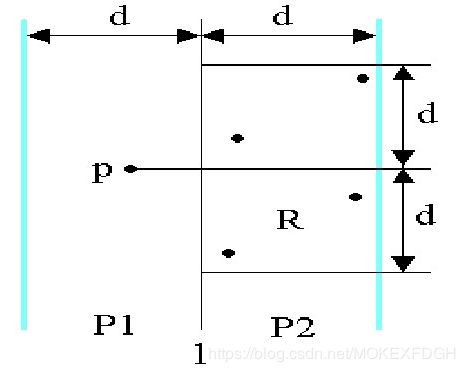
又因为 P2 中的点对距离都不小于 d,所以极端情况就是 R 的每个角上都有一个点,即最多只有 6 个点是需要我们计算的 q。
此外,我们可以在计算前,将 P1 和 P2 中的点安装 y 坐标排序,将 p 和 P2 的点投影到 l 上,那么就只要检查 p 点附近距离 d 内的点(最多6个)就行了。
伪代码:
public static double cpair{
n = |S|;
if(n<2)
return -1;
m = S中各点x坐标的中位数。
S1={p∈S|x(p)<=m}, S2={p∈S|x(p)>m}
d1 = cpair(S1);
d2 = cpair(S2);
dm = min(d1,d2);
P1,P2分别是距 l 的距离在 dm 之间的所有点集合
将 P1,P2 依 y 坐标排好序,点列分别为 X,Y
扫描 X,对于 X 的每个点检查 Y 中每个点与其距离在 dm 之内的所有点距离,最小记录为 dl
d = min(dm,dl);
return d;
}