分支定界法——旅行商(TSP)问题

问题描述

给定一个n顶点网络（有向或无向），找出一个包含n个顶点且具有最小耗费的换路。任何一个包含网络所有顶点的换路称为一个旅行。旅行商问题（Traveling Salesman Problem，TSP）是要寻找一条耗费最少的旅行。

               

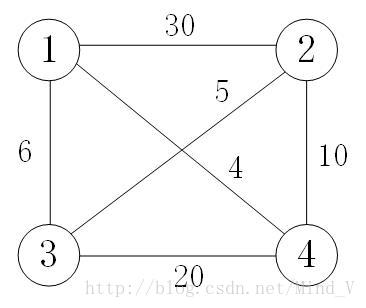
                              图1 四顶点网络

如图1是一个四顶点无向网络。这个网络的一些旅行：1,2,4,3,1；1,3,2,4,1和1,4,3,2,1。旅行1,2,4,3,1的耗费为66,；旅行1,3,2,4,1的耗费为25；旅行1,4,3,2,1的耗费为55.故1,3,2,4,1是网络中耗费最少的旅行。

算法设计

和回溯法解决TSP问题一样，首先确定问题的解空间是一个排列树，从顶点1出发最后回到顶点1，所以排列可以表示为[1,x2,…,xn,1]。和子集树一样，使用一个优先级队列求解。要求旅行的耗费最小，故使用小根堆储存活动节点，堆中每个活动节点的子树耗费所能取得的下界lowerCost 是优先级队列的优先级，即当前节点确定的途径下继续完成排列能取得最低耗费（并不一定保证能最终达到这个值）。

每个活动节点是小根堆的一个元素，元素结构包括：

lowerCost;      //当前节点往后排列，整个回路所能取得的总耗费的下限 

currentCost;     //从根到当前节点的当前排列的耗费 

restMinCost;     //从当前节点到最后一个节点，每个节点的最小出边的耗费之和 

s;               //从根节点到当前节点的路径为[0:s] 

currentTour[];   //从根节点到当前节点的路径(排列)

如何获得lowerCost：
对于每个活动节点，可知当前耗费currentCost，对于剩余的顶点，计算每个顶点的最小出边之和restMinCost即为剩余路径的最小耗费的下界，lowerCost=currentCost + restMinCost。

算法步骤

1、准备工作：建立小根堆，用于存储活动节点。计算每个顶点的最小出边，若存在某个顶点没有出边，则算法终止。初始化树根（顶点1）为第一个活动节点。 

2、判断节点是否是叶结点的父节点：是的话，则检查是否一定有最低耗费，若是加入小根堆； 

3、不是叶结点的父节点，则生成子节点，并判断子节点是否有可能取得最低耗费，若可能则加入小根堆； 

4、取出下一个节点作为活动节点，若该节点已经是叶结点，返回当前最低耗费值，即为最优旅行。若不是叶结点则循环2、3步。

 

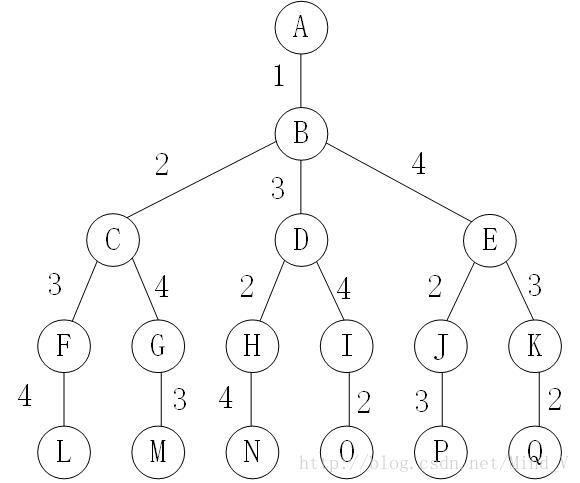
                              图2  四顶点网络的解空间树 

小根堆中的元素变化：{}——>{C,D,E}——>{C,D,K,J}——>{C,K,J,H,I}——>{C,K,J,I,N}——>{C,K,I,N}——>{C,K,I}

最后取出活动节点N，但是N已经是叶结点，故返回最优值25，和最佳途径1->3->2->4->1,并终止算法。

事实上，检查节点J的子节点P时执行的是步骤2，也能得到最优值25，但是由于N已经加入小根堆，并且当前最优值已经是25，所以P没有加入小根堆，途径1->4->2->3->1也就被排除了。

需要注意的是，对于以下的C++程序，需要手动释放掉每个活动节点的数据成员currentTour数组的内寸，包括最后小根堆中剩余的节点。

C++实现

小根堆minHeap元素结构

#pragma once
struct heapNode
{
    int lowerCost;      //当前节点往后排列，整个回路所能取得的总耗费的下限
    int currentCost;    //从根到当前节点的当前排列的耗费
    int restMinCost;    //从当前节点到最后一个节点，每个节点的最小出边的耗费之和
    int s;              //从根节点到当前节点的路径为[0:s]
    int *currentTour;   //从根节点到当前节点的路径(排列)

    //算术运算时的类型转换
    operator int() { return lowerCost; }

    //重载大于号运算符，用于小根堆比较
    bool operator>(const heapNode &right)
    {
        return lowerCost > right.lowerCost;
    }
};

小根堆minHeap 部分源码

#pragma once
#include
#include 

using namespace std;

template<class T>
void changeLength1D(T*& a, int oldLength, int newLength)
{
    if (newLength < 0)
    {
        cout << "new length must be >= 0" << endl;
        exit(1);
    }

    T* temp = new T[newLength];              // new array
    int number = min(oldLength, newLength);  // number to copy
    copy(a, a + number, temp);
    delete[] a;                             // deallocate old memory
    a = temp;
}

template<class T>
class minHeap 
{
public:
    minHeap(int initialCapacity = 10);
    ~minHeap() { delete[] heap; }
    bool empty() const { return heapSize == 0; }
    int size() const
    {
        return heapSize;
    }
    const T& top()
    {// return min element
        if (heapSize == 0)
            exit(1);
        return heap[1];
    }
    void pop();
    void push(const T&);
    void initialize(T *, int);
    void deactivateArray()
    {
        heap = NULL; arrayLength = heapSize = 0;
    }
    void output(ostream& out) const;
private:
    int heapSize;       // number of elements in queue
    int arrayLength;    // queue capacity + 1
    T *heap;            // element array
};

template<class T>
minHeap::minHeap(int initialCapacity)
{// Constructor.
    if (initialCapacity < 1)
    {
        cout << "Initial capacity = " << initialCapacity << " Must be > 0";
        exit(1);
    }
    arrayLength = initialCapacity + 1;
    heap = new T[arrayLength];
    heapSize = 0;
}

template<class T>
void minHeap::push(const T& theElement)
{// Add theElement to heap.

 // increase array length if necessary
    if (heapSize == arrayLength - 1)
    {// double array length
        changeLength1D(heap, arrayLength, 2 * arrayLength);
        arrayLength *= 2;
    }

    // find place for theElement
    // currentNode starts at new leaf and moves up tree
    int currentNode = ++heapSize;
    while (currentNode != 1 && heap[currentNode / 2] > theElement)
    {
        // cannot put theElement in heap[currentNode]
        heap[currentNode] = heap[currentNode / 2]; // move element down
        currentNode /= 2;                          // move to parent
    }

    heap[currentNode] = theElement;
}

template<class T>
void minHeap::pop()
{// Remove max element.
 // if heap is empty return null
    if (heapSize == 0)   // heap empty
    {
        cout << "heap is empty!" << endl;
        exit(1);
    }

    // Delete min element
    heap[1].~T();

    // Remove last element and reheapify
    T lastElement = heap[heapSize--];

    // find place for lastElement starting at root
    int currentNode = 1,
        child = 2;     // child of currentNode
    while (child <= heapSize)
    {
        // heap[child] should be smaller child of currentNode
        if (child < heapSize && heap[child] > heap[child + 1])
            child++;

        // can we put lastElement in heap[currentNode]?
        if (lastElement <= heap[child])
            break;   // yes

                     // no
        heap[currentNode] = heap[child]; // move child up
        currentNode = child;             // move down a level
        child *= 2;
    }
    heap[currentNode] = lastElement;
}

TSP算法程序

#include
#include"heapNode.h"
#include"minHeap.h"
#define N 5

//全局变量
int n = N - 1;
int cost[N][N];  //cost[1:n][1:n] 表示城市之间的旅行耗费，不存在路径则耗费等于-1
int bestTour[N];

int TSP(int *bestTour)
{//最小费用分支定界代码，寻找最短旅行
 //bestTour[1:n]存储最短旅行路径

    minHeap liveNodeMinHeap;

    //costOfMinOutEdge[i]表示顶点i的最小出边
    int *minCostOutEdge = new int[n + 1];
    int sumOfMinCostOutEdges = 0;
    for (int i = 1; i <= n; ++i)
    {
        int minCost = -1;
        for (int j = 1; j <= n; ++j)
            if (cost[i][j] != -1 && (minCost == -1 || minCost > cost[i][j]))
                minCost = cost[i][j];
        if (minCost == -1)
            return -1;
        minCostOutEdge[i] = minCost;
        sumOfMinCostOutEdges += minCost;
    }

    //初始E-节点的根
    heapNode eNode;
    eNode.lowerCost = sumOfMinCostOutEdges;
    eNode.currentCost = 0;
    eNode.restMinCost = sumOfMinCostOutEdges;
    eNode.s = 0;
    eNode.currentTour = new int[n];
    //初始化排列为[1,2,3,...,n,1]
    for (int i = 0; i < n; ++i)
        eNode.currentTour[i] = i + 1;

    int bestCostSoFar = -1;  //当前最佳旅行耗费
    int *currentTour = eNode.currentTour;

    //搜索排列树
    while (eNode.s < n - 1)
    {
        currentTour = eNode.currentTour;
        if (eNode.s == n - 2)
        {//叶结点的父节点
         //检查是否为当前最优旅行
            if (cost[currentTour[n - 2]][currentTour[n - 1]] != -1 &&
                cost[currentTour[n - 1]][1] != -1 &&
                (bestCostSoFar == -1 || eNode.currentCost +
                    cost[currentTour[n - 2]][currentTour[n - 1]] +
                    cost[currentTour[n - 1]][1] < bestCostSoFar))
            {//发现最优旅行，加入小根堆
                bestCostSoFar = eNode.currentCost +
                    cost[currentTour[n - 2]][currentTour[n - 1]] +
                    cost[currentTour[n - 1]][1];
                eNode.currentCost = bestCostSoFar;
                eNode.lowerCost = bestCostSoFar;
                eNode.s++;
                liveNodeMinHeap.push(eNode);
            }
            else
            {
                delete[] eNode.currentTour;  //舍弃非最优的叶结点的父节点，释放内存
                eNode.currentTour = nullptr;
            }
        }

        else
        {//生成子节点
            for(int i = eNode.s + 1; i < n; ++i)
                if (cost[currentTour[eNode.s]][currentTour[i]] != -1)
                {//子节点可行
                    int currentCost = eNode.currentCost +
                        cost[currentTour[eNode.s]][currentTour[i]];
                    int restMinCost = eNode.restMinCost -
                        minCostOutEdge[currentTour[eNode.s]];
                    int leastCostPossible = currentCost + restMinCost;

                    if (bestCostSoFar == -1 ||
                        leastCostPossible < bestCostSoFar)
                    {//子树可能有更优的叶结点，把当前子树的根放入小根堆
                        heapNode hNode;
                        hNode.lowerCost = leastCostPossible;
                        hNode.currentCost = currentCost;
                        hNode.restMinCost = restMinCost;
                        hNode.s = eNode.s + 1;
                        hNode.currentTour = new int[n];
                        copy(currentTour, currentTour + n, hNode.currentTour);

                        swap(hNode.currentTour[hNode.s], hNode.currentTour[i]);
                        liveNodeMinHeap.push(hNode);
                    }
                }

            //完成节点扩展，释放内存
            delete[] eNode.currentTour;
            eNode.currentTour = nullptr;
        }

        if (liveNodeMinHeap.empty())
            break;

        //取下一个E-节点
        eNode = liveNodeMinHeap.top();
        liveNodeMinHeap.pop();
    }

    if (bestCostSoFar == -1)
        return -1;

    //复制到bestTour
    copy(eNode.currentTour, eNode.currentTour + n, bestTour + 1);

    //释放小根堆中剩余元素的currentTour数组内存***虽然小根堆析构，
    //但是currentTour是new的内存，依然存在，故必须手动释放
    while (true)
    {
        delete[] eNode.currentTour;
        if (liveNodeMinHeap.empty())
            break;
        //取下一个E-节点
        eNode = liveNodeMinHeap.top();
        liveNodeMinHeap.pop();
    }

    return bestCostSoFar;
}

void init()
{
    cost[1][1] = -1;
    cost[1][2] = 30;
    cost[1][3] = 6;
    cost[1][4] = 4;

    cost[2][1] = 30;
    cost[2][2] = -1;
    cost[2][3] = 5;
    cost[2][4] = 10;

    cost[3][1] = 6;
    cost[3][2] = 5;
    cost[3][3] = -1;
    cost[3][4] = 20;

    cost[4][1] = 4;
    cost[4][2] = 10;
    cost[4][3] = 20;
    cost[4][4] = -1;
}
void main()
{
    init();

    int bestCost = TSP(bestTour);  //起点定为1，从第二层开始  

    cout << "最少的运费为:" << bestCost << endl;
    cout << "最佳路径为: ";

    copy(bestTour + 1, bestTour + n + 1, ostream_iterator<int>(cout, "->"));
    cout << bestTour[1] << endl;
}

测试结果

最少的运费为:25
最佳路径为: 1->3->2->4->1
请按任意键继续. . .