[从零构建光栅渲染器] 4.透视投影

[从零构建光栅渲染器] 4.透视投影

非常感谢和推荐Sokolov的教程，Sokolov使用500行C++代码实现一个光栅渲染器。教程学习过程非常平滑，从画点、线和三角形开始教学，在逐步深入三维变换，投影，再到顶点着色器，片段着色器等等。教程地址：https://github.com/ssloy/tinyrenderer。Sokolov的教程为英文，我翻译了其文章。

在学习过程中，有些内容可能您可能云里雾里，这时就需要查阅《计算机图形学》的书籍了，这里面的算法和公式可以帮助您理解代码。

作者：憨豆酒（YinDou），联系我[email protected]，熟悉图形学，图像处理领域，本章的源代码可在此仓库中找到https://github.com/douysu/person-summary：如果对您有帮助，还请给一个star，如果大家发现错误以及不合理之处，还希望多多指出。

我的知乎
我的Github
我的博客

本章运行结果

提醒：

翻译作者内容：相比上一章，本章的渲染效果加上了投影。如果本章内容有看不懂的地方，建议找一本图形学的书籍阅读一下变换部分，或者阅读LearnOpenGL上面的教程。

已经有很多中文资料讲解变换和投影了，可以配合着中文资料来学习本章。

目标

在前面的课程中，我们通过简单地忘记z坐标，用正投影的方式渲染了模型，今天我们学习如何使用透视除法。

2D几何

一个平面上的线性变换可以用对应的矩阵表示，如果我们取一个点(x,y)，那么它的变换可以写成如下所示。

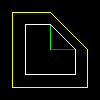
比较简单的变换是本身的变换，矩阵不移动任何点。

矩阵的对角线系数给出了沿坐标轴的缩放比例。让我们举例说明一下，如果我们进行以下变换：

然后，白色物体(被砍掉一个角的白色方块)将被转化为黄色物体。红色和绿色的线段分别给出单位长度的向量，分别与x和y对齐。

文章使用的图像生成代码在这里。this code.

我们为什么要用矩阵？因为它很方便。首先，用矩阵的形式，我们可以这样表达整个对象的变换。

在这个表达式中，变换矩阵与前一个表达式相同，但2x5矩阵除了我们的方块状对象的顶点外，其他的都不是什么。我们只需把数组中的所有顶点都拿出来，乘以变换矩阵，就得到了变换后的对象。很酷吧？

那么，真正的原因就隐藏在这里：很多时候，我们希望在一连串的变换中，用很多变换来变换我们的对象。想象一下，在你的源码中，你写的变换函数像：

vec2 foo(vec2 p) return vec2(ax+by, cx+dy);
vec2 bar(vec2 p) return vec2(ex+fy, gx+hy);
[..]
for (each p in object) {
    p = foo(bar(p));
}

这段代码对我们的对象的每个顶点进行两次线性变换，往往我们计算这些顶点的次数是以百万计。而且一排几十次变换的情况并不罕见，导致几千万次的运算，真的很浪费资源。在矩阵形式下，我们可以将所有的变换矩阵进行预乘，对我们的对象进行一次变换。对于一个只有乘法的表达式，我们可以把括号放在想放的地方，是不是？

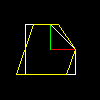
好了，让我们继续说下去。我们知道，矩阵的对角线系数是沿着坐标轴对我们的对象进行缩放。那么其他系数的作用是什么呢？让我们考虑一下下面的变换。

结果成这样：

这是一个简单的沿x轴的错切，另一个反对角元素沿着y轴错切空间。因此，在一个平面上有两个基础线性变换：缩放和错切。很多读者反映，那旋转呢？

原事实证明，任何旋转（绕原点旋转）都可以表示为三个错切的组合动作，这里白色对象被转换为红色对象，然后转换为绿色对象，最后转换为蓝色对象：

但这些就很复杂了，为了让事情简单，我们直接写一个旋转矩阵。

翻译作者内容：可以查看图形学的书籍变换的内容。

我们可以按照任意顺序进行乘法，但我们要记住，对于矩阵的乘法是不换向的。

这句话是有道理的：错切一个物体，然后再去旋转它，和旋转后再去错切它是不一样的!

翻译作者内容：在线性代数中学习过，矩阵相乘是不可逆的。

2D 仿射变换

所以，平面上的任何线性变换都是由缩放和错切变换组成的。而这意味着，我们可以做任何线性变换，原点永远不会移动! 这些可行性是很大，但如果我们不能进行简单的变换，我们的编程就很难过。我们能做到吗？好吧，平移不是线性的，没问题，让我们在执行完线性部分后，再尝试着进行附加平移。

这个表达方式真的很酷。我们可以进行旋转、缩放、错切和平移。然而，让我们回想一下，我们感兴趣的是组成多个变换。下面是两个变换的组成是什么样子的（记住，我们需要组成几十个这样的变换）。

只是一个顶点（x，y）变换就得嵌套这么多层，这显然是不行的。

下面我们就想办法换成一个矩阵。

齐次坐标

好了，现在是黑魔法的时候了。想象一下，我在我们的变换矩阵中加入一列，一列（从而使其成为3x3），并将一个坐标始终等于1的坐标附加到要变换的向量上。例如下面这样。

如果我们把这个矩阵和向量乘以1，我们就会得到另一个向量，最后一个分量中的1，但另外两个分量的形状和我们想要的完全一样很神奇。观察到与上一节的计算结果是相同的。

事实上，这个想法其实很简单。平行平移在2D空间中不是线性的。所以我们把我们的2D空间嵌入到3D空间中（只需在第3个分量中加1即可）。也就是说，我们的2D空间就是3D空间中的平面z=1。然后我们进行线性三维变换，并将结果投影到我们的二维物理平面上。平行变换并没有变成线性变换，但流水线很简单。

我们如何将3D投影到2D平面上？很简单，就是用3D分量进行除法。

等一下，禁止除以0！

谁说的这个。让我们回顾一下管线

• 我们将2D嵌入到3D中，将其嵌入到z=1的平面内。
• 我们可以在3D中为所欲为
• 对于每一个要从三维投影到二维的点，我们在原点和要投影的点之间画一条直线，然后找到它与平面z=1的交点。

在这个图像中，我们的二维平面是品红色的，点(x,y,z)被投影到(x/z,y/z)上。

让我们想象一下点（x，y，1）垂直投影会投影到哪里？答案是在（x，y）平面上：

现在让我们下降到轨道上，例如，将点（x，y，1/2）投影到（2x，2y）上：

让我们继续，点(x,y,1/4) 成为(4x, 4y):

如果我们继续这个过程，接近z=0，那么投影就会在(x,y)的方向上离原点更远。换句话说，点(x,y,0)在(x,y)的方向上被投影到一个无限远的点上。它是什么呢？对了，它只是一个向量!

齐次坐标可以区分向量和点。如果一个程序员写了vec2(x,y)，那么它到底是向量还是点呢？很难说。结论就是：在齐次坐标中，所有z=0的东西都是向量，其余的都是点。看：向量+向量=向量。向量-向量=向量。点+向量=点。这样比较好，不是吗？

综合变换

正如我之前说的，我们应该积累数十个转换。什么要这样做？让我们想象一下，我们需要将一个物体（2D）围绕一个点（x0,y0）旋转。怎么做呢？我们可以在某处查找公式，或者我们可以自己去完成，我们需要的工具都有了!

在3D中，动作的序列会有点长，但想法是一样的：我们需要知道一些基本的变换，在它们的帮助下，我们可以表示任何组成的动作。

翻译作者内容：先平移，在旋转，在平移回来就完成了。

等一下，3×3矩阵的底部是做什么用的呢

这部分比较难理解，推荐看这里。https://zhuanlan.zhihu.com/p/66384929

对角线是缩放，右边是平移，那下面的内容是干什么用的呢。

当然可以！让我们将以下转换应用于我们的标准方形对象：

回想一下原始对象是白色的，单位轴矢量是红色和绿色的：

这是转换后的：

这里又发生了另一种有意思的事情（白色！）。你还记得我们的y-buffer练习吗？这里我们也要做同样的练习：我们把二维物体投射到垂直线x=0上，让我们把规则变困难一点：我们必须使用中心投影，我们的相机在点(5,0)上，并指向原点。为了找到投影，我们需要在摄像机和要投影的点（黄色）之间画出直线，并找到与屏幕线的交点（白色垂直）。

现在，我用转换后的对象代替原来的对象，但我不碰我们之前画的黄色线条：

如果我们用标准的正交投影法将红色物体投射到屏幕上，那么我们就会发现完全一样的点! 让我们仔细观察一下变换的工作原理：所有的垂直段都会被变换成垂直段，但靠近摄像头的部分会被拉伸，而远离摄像头的部分会被缩小。如果我们正确地选择系数（在我们的变换矩阵中是-1/5系数），我们就会得到一个透视（中心）投影的图像！如果我们正确地选择系数，我们就会得到一个透视（中心）投影的图像。

到3D空间工作了

让我们解释一下其中的奥妙。对于二维仿射变换，对于三维仿射变换，我们将使用齐次坐标：将一个点(x,y,z)用1(x,y,z,1)增强，然后在4D中进行变换，再投射回三维。例如，如果我们取下面的变换。

逆向投影给了我们以下的三维坐标。

让我们记住这个结果，但暂时把它放在一边。让我们回到中心投影的标准定义，没有任何花哨的东西作为4D变换。给定一个点P=(x,y,z)，我们要把它投影到z=0的平面上，相机在z轴上的点(0,0,c)。

三角形ABC和ODC是相似的。这意味着我们可以写出以下的内容。 |AB|/|AC|=|OD|/|OC| => x/(c-z) = x’/c。换句话说，就是：

通过对三角形CPB和CP’D进行同样的推理，很容易找到下面的表达式。

这真的和我们刚才的结果很相似，但是在那里我们通过一个矩阵乘法得到了结果。我们得到了系数的规律：r=-1/c。

让我们总结我们今天学习的公式

如果你在不理解上面的材料的情况下就简单地复制粘贴这个公式，我恨死你了。

所以，如果我们想用一个位于z轴上的摄像头（重要！）相机在距离原点c的z轴上，计算出一个中心投影，那么我们把这个点用1的方法将其增强到4D中，然后用下面的矩阵乘以1，再将其逆向投影到3D中。

我们对我们的对象进行了变形，只需忘记它的Z坐标，我们就可以得到一个透视画。如果我们要使用z-buffer，那么自然也不要忘记z。