从最长回文串到贪心和动态规划(1)
可以去https://segmentfault.com/a/1190000003914228看原版,但是有些方面感觉我解释的要更多一些,同时改正了一处错误。
问题定义:
最长回文串问题:给定一个字符串,求出它的最长回文串长度。
如果一个字符串正着读和反着读是一样的,那么它就是回文串。
比如:
12321 a aba aaaa tattattattat
1. Brute-force:
最简单粗暴的解法:找到字符串的所有子串,遍历每一个子串以验证它们是否为回文串。
一个子串由起点和终点决定,因此对于一个长度为n的字符串,一共有![]() 个子串,这些子串的平均长度大约是n/2,所以这个解法的时间复杂度为
个子串,这些子串的平均长度大约是n/2,所以这个解法的时间复杂度为![]()
2. 改进的方法:
显然,对于所有的回文串都是对称的!
长度为奇数的回文串以中间字符为对称轴左右对称,长度为偶数的回文串的对称轴在中间两个字符之间的空隙。能否利用这个性质来提高效率呢?当然!
我们知道整个字符串中的所有字符以及字符间的空隙,都可能是某个回文串的对称轴位置-----我们可以遍历这些位置,在每个位置上同时向左右两边扩展,直到左右两边的字符不相同或者是达到边界为止。对于一个长度为n的字符串,这样的位置一共有n + n - 1 = 2n -1个,在每个位置上大约平均要进行n/4(就是n/2之后再/2)次字符比较,于是此算法的时间复杂度为![]() .
.
3. Manacher算法(马拉车算法)
对于一个较长的字符串,上面的复杂度是难以接受的,Can we do better?
来看看解法二存在的缺陷:
- 由于回文串长度的奇偶性造成了不同性质的对称轴位置,解法二要对奇偶两种情况分别处理
- 很多子串被重复访问很多次,造成较差的时间复杂度。
缺陷2可以这样看出来:
char: a b a b a
i : 0 1 2 3 4当i == 1或者 i== 2的时候,子串aba都被遍历了一次,一个是 aba 一个是 ababa
Manacher算法就是来搞定解法二的缺陷的!
改进1. 解决长度奇偶性带来的对称轴位置问题:
Manacher算法首先对字符串做一个预处理(就像机器学习在开始时,对输入数据进行处理一样),在所有空隙位置,包括首尾插入同样的符号,要求这个符号不会在原串中出现,使得所有串都是奇数长度的。比如:
aba -> #a#b#a
abba -> #a#b#a#b#插入同样的符号,且符号不存在原串之中,因此子串的回文性不受影响。
改进2. 解决重复访问子串的问题:
回文半径:把回文串中左边或者最右边位置与对称轴的距离称之为回文半径。
Manacher定义了一个回文半径数组RL,用RL[i]表示第i个字符为对称轴的回文串的回文半径。我们一般对字符串从左向右处理,因此这里定义RL[i]为第i个字符为对称轴的回文串 和 最右一个字符(回文串)的距离。举例说明如下:
char : # a # b # a #
RL : 1 2 1 4 1 2 1
RL-1 : 0 1 0 3 0 1 0
i : 0 1 2 3 4 5 6
char : # a # b # b # a #
RL : 1 2 1 2 5 2 1 2 1
RL-1 : 0 1 0 1 4 1 0 1 0
i : 0 1 2 3 4 5 6 7 8上面我们还求了一个RL-1,发没发现,这个RL[i]-1的值,正是原来那个没有插入过分隔符的字符串中,以位置i为对称轴的最长回文串的长度。那么只要我们求出了RL数组,我们就能得到最长回文子串的长度。
于是,我们把求最长回文串的问题转化成为了怎样高效的求RL数组的问题。基本思路就是:利用回文串的对称性,扩展回文串
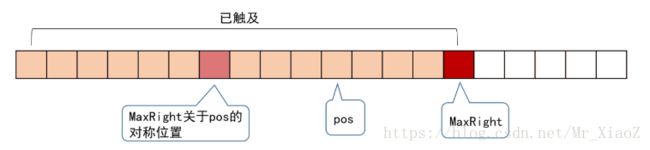
我们再引入一个辅助变量MaxRight,MaxRight表示当前访问到的所有回文子串,所能触及的最右一个字符的位置。
另外还要记下MaxRight对应的回文串的对称轴所在的位置,记为pos,他们的关系如下:
我们从左往右地访问字符串来求RL,假设当前访问到的位置为i,即要求RL[i],在对应上图,i必然是pos的右边,但我们更关注的是:
i是在MaxRight的右边还是左边???
下面就是大家迷糊的开始:
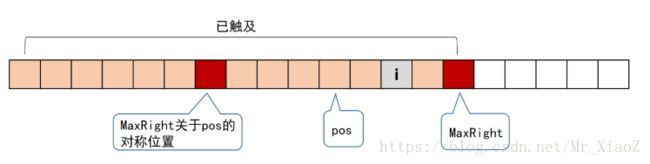
1) 当i在MaxRight的左边,也就是下图这样:
其实在上图中我们可以得出来一些信息:MaxRight是回文子串所能到达的最右端,pos是以MaxRight为最右端的回文子串的对称轴,pos的左右两侧是回文串(最右端可达MaxRight),也就是两个红色块之间的部分是属于回文串的,并且以i为对称轴的回文串是和红色块之间的回文串是有重叠的。
我们找到i关于pos的对称位置j,这个j对应的RL[j]是算过的,根据回文串的对称性,以i为对称轴的回文串和以j为对称轴的回文串,有一部分是相同的。这又有两个细分:
1. 以j为对称轴的回文串很短,就像下面这样:
这时候我们知道,RL[i]至少不会小于RL[j]的(两个红色块之间包括红色块是回文的嘛),我们就可以令RL[i] = RL[j],但是以i为对称轴的回文串可能更长(因为最远的MaxRight对应的对称轴不过是pos,是在i的左面,当然不否认以i为对称轴的回文串最长可能就像上图一样没到MaxRight),因此我们试着以i为对称轴,继续往左右两边扩展,直到左右两边字符不同,或者是达到边界。然后更新MaxRight和pos。
2. 以j为对称轴的回文串很长,像下面一样长:
注意哈,上面的带箭头的两个蓝线是对的(原文这里标注有问题),中间的虚蓝线忽略。
这时,我们只能确定,两条蓝线之间的部分,也就是不超过MaxRight的部分是回文的(解释一下,j是i关于pos对称的,j在最左边的红块到蓝块(pos)之间(包括红块不包括蓝块)是回文的两个红块之间又都是回文串,所以可以知道i为对称轴的回文串最起码可以是蓝块pos到最右边红块MaxRight(包括红块MaxRight不包括蓝块)),于是从这个长度开始,尝试以i为中心向左右两边扩展,直到左右两边字符不同,或者达到边界。然后更新MaxRight和pos。
其实不管上面1,2哪种情况,之后都要尝试更新MaxRight和pos,因为有可能得到更大的MaxRight。
具体操作:
1. 令RL[i] = min(RL[2 * pos - i], MaxRight - i)
2. 以i为中心扩展回文串,直到左右两边字符不相同或者达到边界
3. 更新MaxRight和pos
Note:读者可以想一下 为什么令RL[i] = min(RL[2 * pos - i], MaxRight - i),提示一下:
RL[2 * pos - i] 对应于以j为对称轴的回文串较短(以j为对称轴的回文串的最右边没有超过pos)
MaxRight - i 对应于以j为对称轴的回文串较长(以j为对称轴的回文串的最右边超出了pos)2)当i在MaxRight的右边
遇到这种情况,说明以i为对称轴的回文串还没有任何一个部分被访问过,于是只能从i的左右两边开始尝试扩展了,当左右两边字符不同,或者到达字符串边界时停止。然后更新MaxRight和pos。
代码:
def manacher(arr):
# 预处理字符串,解决字符串长度为奇偶带来的对称轴的不统一问题
# 注意这里的前后两个#以及join()的用法,默认就是以空格隔开的
arr = '#'+ '#'.join(s) +'#'
# 初始化三个所需要的变量:RL[], MaxRight, pos以及最后输出的MaxLen
# 这里的RL数组初始化的方法不错,可以借鉴一下
RL = [0] * len(arr)
MaxRight = 0
pos = 0
MaxLen = 0
# 从头到尾循环
for i in range(len(arr)):
# 假如在i在MaxRight的左边,对应于j较短or较长两种情况,取其min即可,向两边拓展
if i < MaxRight:
RL[i] = min(RL[2*pos - i], MaxRight - i)
# 否则当i在MaxRigth的右边的时候,i为对称轴的回文串还没有任何一个部分被访问过,故从1开始
else:
RL[i] = 1
# 这里就是开始向两边拓展,遇到左右两边不相等或者边界的时候就停止
# i - RL[i] >= 0 i为对称轴的回文串最长也只是从开头到i位置的长度,所以一定要>=0
# i + RL[i] 不能超出边界,就是以i为对称轴,RL[i]为回文半径的和不能越界
# RL[i - RL[i]] == RL[i + RL[i]]:以i为对称轴,回文半径一点点向外扩展
while i - RL[i] >= 0 and i + RL[i] < len(arr) and arr[i - RL[i]] == arr[i+RL[i]]:
RL[i] += 1
# 勿忘更新MaxRight和pos
if RL[i] + i - 1 > MaxRight:
MaxRight = RL[i] + i -1
pos = i
# MaxLen就是之前的回文半径和现在以i为对称轴的回文半径取个max
MaxLen = max(MaxLen, RL[i])
# 这里的要-1,勿忘,和RL[i]-1才是最长回文串的长度一样
return MaxLen - 1复杂度分析
空间复杂度:插入分隔符形成新串,占用了线性的空间大小;RL数组也占用线性大小的空间,因此空间复杂度是线性的。
时间复杂度:尽管代码里面有两层循环,通过amortized analysis(均摊分析)我们可以得出,Manacher的时间复杂度是线性的。由于内层的循环只对尚未匹配的部分进行,因此对于每一个字符而言,只会进行一次,因此时间复杂度是O(n)。