cs231n学习笔记——图像分类

写在前面的废话

在机器学习和深度学习的道路上一直在当混子，丧了很久决定。决定从新出发，决定好好学习下经典的cs231n 2017的课程（2019英语水平的原因暂时啃不动），写博客可能更多的原因并不是想分享给别人看的，而是写给自己的，算是学后总结吧。在这里还是要感谢为cs231n课程做了精心翻译的人。在下面附上链接，我也是在看了视频后，又反过来看他做的翻译笔记重新梳理复习的。接下来的顺序也是根据课程讲解的知识顺序进行整理的，一些自己的理解和原来错误的认识我也会写出来的。

CS231n课程笔记翻译：https://zhuanlan.zhihu.com/p/20894041?refer=intelligentunit

1.图像分类

其实图像分类的原理更像是再教小孩子，你拿很多的球（也可以是别的）到孩子面前，告诉他教他哪些是篮球、哪些是足球、哪些是网球等等。之后呢，你又拿了一个其他的球，让孩子来通过刚才学习的经验分辨这个是什么球。图像分类就是这样：就是用已有固定的分类标签集合，然后对于输入的图像，从分类标签集合中找出一个分类标签，最后把分类标签分配给该输入图像。

下面来举个例子：首先科普一下，我们计算机中打开一张彩色图片，宽248像素，高400像素。这个图片包含了三个维度的信息，长x宽x3(RGB这个3代表的是红、绿和蓝3个颜色通道)。所以当我们写代码将一张图片加载后就形成了一个248X400X3=297600个元素的数组。每个元素的范围是0~255，因为每个像素点颜色范围不会超过255，0代表黑，255代表白。就是下面这个样子。

这个打开后看到的这堆乱七八糟的数字。举个类似的例子，其实就是像生物的DNA，现在图像分类要做的就是根据这些DNA来分辨，打开的这个图片是什么物种。识别的难点我就不说了，人有分不清的时候机器就更分不清了：例如角度变化、光线、变形等等。

2.数据驱动

课程讲到数据驱动的时候，我明显感觉眼前一亮，一个很恰当的词语。理解上讲，就是以往我们在做算法实现去识别某一个事物的时候，都是根据这个东西的特性量身去定制。但是我们觉得这样很麻烦，我们希望我给你什么东西，你就能自己根据我给你的变化识别。还是拿孩子的例子，就是我给你什么你就根据我给你的东西去学习分辨，你能够学到什么完全是由我给你的东西决定的。数据驱动就是这个道理。用数据驱动填充模型，也决定了模型能够识别什么东西。

3.图形分类流程

输入：输入N个图片的集合，其中每张图片标签（类别）是已知的。这个集合叫做训练集。
训练：训练其实就是学习一个分类器，使用输入的训练集来学习如何判断各个分类。
预测与评价：给定一张没见过的图片，让模型来预测是哪个分类标签。然后根据它分类的正确与否我们来评价这个分类器的质量。

4.L1距离（曼哈顿距离）

曼哈顿距离其实是一种坐标距离，表示在标准坐标轴上的轴距绝对值。在模型之间使用曼哈顿距离往往样本具有某些重要意义的特征值，更适合用到这个距离，例如1个人的工资条，其中有工龄、收入、职位等等。每个特征都代表了这个人的某种身份，而计算2个人之间的样本距离，曼哈顿是比较合适的。下面是计算公式：
$$d(I_1,I_2)=\sum _p|I_1^P-I_2^P|$$

可以看得出L1距离取决于你选择的坐标系，一旦你转动坐标系，两点之间的距离就会随之发生变化。而相比L2距离就不存在这个问题，你可以随意转动坐标轴，两点的距离都是确定的。

5.L2距离（欧氏距离）

欧式距离我就不多解释了，初中就学过了。
$$d(I_1,I_2)=\sqrt{\sum _P(I_1^P-I_2^P{)}^2}$$

这里比较有趣的就是模型选择到底用哪个距离进行计算，这就要看实际情况来进行取舍了。两个距离都不存在谁更好的问题，如果把握不准的话就都试一试。

6. Nearest Neighbor分类器

首先我先讲一下这个近邻（Nearest Neighbor）算法的优缺点，下面的K近邻同样适用这个优缺点。
优点:

• 简单，无需预训练
• 无需调参

缺点：

• 需要更多的训练数据才能改善模型，而且可能导致维度灾难。
• 计算成本高，需要计算到每个样本之间的距离。

这个模型很是辣鸡，就是因为它比较简单，更适合教学讲解。而且几乎不会再实际中使用，为什么呢？而与它相反的例子是：卷积神经网络，在一般为用户提供使用的模型都是训练好的，所以往往公司会花大量的时间去提前训练好模型，在使用过程中直接进行分类即可速度非常快，不会占用用户太多空间和时间。而NN模型所谓的训练其实就是把所有的数据保存起来，进行预测的时候，要实时化大量时间去计算，这样的方式简直是不可接受的。下面在介绍模型前，先介绍两个相关概念，因为之后模型会用到，而且这两个都是可以根据实际情况搭配使用的。
———————————————————————————

1.CIFAR-10数据集说明

这里在验证Nearest Neighbor分类器的时候使用了CIFAR-10数据集。
CIFAR-10：CIFAR-10数据集包含10个类别的60000个32x32彩色图像，有50000张训练图像和10000张测试图像。这个数据集包含了10种分类标签，每个类别6000个图像。下图中你可以看见10个类的10张随机图片。

左边：从CIFAR-10数据库中的样本图像。右边：第一列是输入模型的测试图像，然后第一列的每个测试图像右边是使用Nearest Neighbor算法，从训练集中选出的10张最类似的图片。由于图不是很清楚就直接说，上面10个分类中，只有3个是准确的。

那么如何比较距离呢？就是将每张图片转化成向量（张量）然后使用L1距离进行运算。向量中的每个数值做减法。

得到的456就是，两张图片的距离，差别越大数值越大。如果数值为0那么就可以认为这两张图片是一模一样的了。
———————————————————————————
大致讲一下过程，首先我们把50000张的训练集，拿给Nearest Neighbor分类器进行训练（其实就是存起来了），之后用10000张的测试集，去挨个和训练集进行距离比较。然后每张测试图片会把，存储训练集的所有图片中和自己距离最小的那张的标签，赋给自己，这就是预测的标签。
———————————————————————————

2.NN代码实现

下面代码实现和讲解部分，课程笔记讲的很清楚，我就直接给考过来了。
下面，让我们看看如何用代码来实现这个分类器。首先，我们将CIFAR-10的数据加载到内存中，并分成4个数组：训练数据和标签，测试数据和标签。在下面的代码中，Xtr（大小是50000x32x32x3）存有训练集中所有的图像，Ytr是对应的长度为50000的1维数组，存有图像对应的分类标签（从0到9）：

# CIFAR10数据读取这部分代码课程上没有，我在这里补充好了。
def load_CIFAR10(path):
	# path = './cifar-10-batches-py/'
    Xtr, Ytr, Xte, Yte = [], [], [], []
	
    for i in range(1, 6):
        filename = os.path.join(path, 'data_batch_%d' % i)
        with open(filename, 'rb') as f:
            data = pickle.load(f, encoding='latin1') # 读取训练集
            Xtr.extend(data['data'])
            Ytr.extend(data['labels'])

    with open(os.path.join(path, 'test_batch'), 'rb') as f:
        data = pickle.load(f, encoding='latin1') # 读取测试集
        Xte.extend(data['data'])
        Yte.extend(data['labels'])
    return np.array(Xtr), np.array(Ytr), np.array(Xte), np.array(Yte)
    
Xtr, Ytr, Xte, Yte = load_CIFAR10('data/cifar10/') # a magic function we provide
# flatten out all images to be one-dimensional
Xtr_rows = Xtr.reshape(Xtr.shape[0], 32 * 32 * 3) # Xtr_rows becomes 50000 x 3072
Xte_rows = Xte.reshape(Xte.shape[0], 32 * 32 * 3) # Xte_rows becomes 10000 x 3072

现在我们得到所有的图像数据，并且把他们拉长成为行向量了。接下来展示如何训练并评价一个分类器：

nn = NearestNeighbor() # create a Nearest Neighbor classifier class
nn.train(Xtr_rows, Ytr) # train the classifier on the training images and labels
Yte_predict = nn.predict(Xte_rows) # predict labels on the test images

# and now print the classification accuracy, which is the average number
# of examples that are correctly predicted (i.e. label matches)
print 'accuracy: %f' % ( np.mean(Yte_predict == Yte) )

作为评价标准，我们常常使用准确率，它描述了我们预测正确的得分。请注意以后我们实现的所有分类器都需要有这个API:train(X, y)函数。该函数使用训练集的数据和标签来进行训练。从其内部来看，类应该实现一些关于标签和标签如何被预测的模型。这里还有个predict(X)函数，它的作用是预测输入的新数据的分类标签。现在还没介绍分类器的实现，下面就是使用L1距离的Nearest Neighbor分类器的实现套路：

import numpy as np
import pickle
import os

class NearestNeighbor(object):
  def __init__(self):
    pass

  def train(self, X, y):
    """ X is N x D where each row is an example. Y is 1-dimension of size N """
    # the nearest neighbor classifier simply remembers all the training data
    self.Xtr = X
    self.ytr = y

  def predict(self, X):
    """ X is N x D where each row is an example we wish to predict label for """
    num_test = X.shape[0]
    # lets make sure that the output type matches the input type
    Ypred = np.zeros(num_test, dtype = self.ytr.dtype)

    # loop over all test rows
    for i in xrange(num_test):
      # find the nearest training image to the i'th test image
      # using the L1 distance (sum of absolute value differences)
      distances = np.sum(np.abs(self.Xtr - X[i,:]), axis = 1)
      min_index = np.argmin(distances) # get the index with smallest distance
      Ypred[i] = self.ytr[min_index] # predict the label of the nearest example
    
    return Ypred

如果你用这段代码跑CIFAR-10，你会发现准确率能达到38.6%。这比随机猜测的10%要好，但是比人类识别的水平（据研究推测是94%）和卷积神经网络能达到的95%还是差多了。点击查看基于CIFAR-10数据的Kaggle算法竞赛排行榜。

**距离选择：**计算向量间的距离有很多种方法，另一个常用的方法是L2距离，从几何学的角度，可以理解为它在计算两个向量间的欧式距离。公式在上面已经介绍过了。
换句话说，我们依旧是在计算像素间的差值，只是先求其平方，然后把这些平方全部加起来，最后对这个和开方。在Numpy中，我们只需要替换上面代码中的1行代码就行：

distances = np.sqrt(np.sum(np.square(self.Xtr - X[i,:]), axis = 1))

注意在这里使用了np.sqrt，开根号其实可有可无，因为他是个单调函数，如果开根号虽然数值变了但是整体都变大了，但是排列分布还会保持一致。

L1和L2比较。比较这两个度量方式是挺有意思的。在面对两个向量之间的差异时，L2比L1更加不能容忍这些差异。也就是说，相对于1个巨大的差异，L2距离更倾向于接受多个中等程度的差异。L1和L2都是在p-norm常用的特殊形式

7. K Nearest Neighbor分类器

Nearest Neighbor分类器如何在进行优化呢？可以看出Nearest Neighbor分类器在进行标签判别的时候是寻找离自己距离最近的一张图片，那么如果选择多张图片是不能能够带来更大的泛化能力呢？K Nearest Neighbor分类器就很自然的被想到了。道理很简单，将距离自己一张图片的判别换成通过离自己最近的K张图片，然后再通过多数投票的方式产生，标签这样能带来更好的泛化能力。

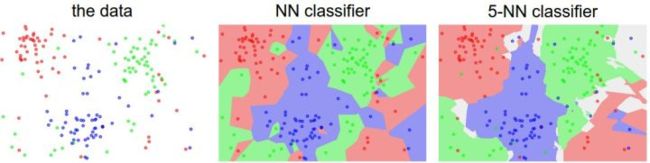
最左边的是原始数据的分布，中间的是Nearest Neighbor分类器的效果图，最右边的是5-Nearest Neighbor分类器的效果图。数据包括3类（红绿蓝）不同的颜色代表不同的决策边界。可以看得出5NN的边界效果更加的圆滑，而且NN分类器产生的不正确的数据孤岛（蓝色区域里包裹的绿色区域），5NN对它做了平滑，能够更加包容异常点，带来了更好的泛化能力。而5NN的白色区域代表着模糊的决策区域，例如投票的分类绿色2个，红色2个，蓝色1个。

1.确定K的值（超参数）

超参数简单理解就是，需要我们进行调优不断尝试变换的参数或者是不同函数例如：L1、L2距离。那么KNN中的K其实就是超参数，需要我们进行调优寻找最合适的值。嗯！机器学习和深度学习其实就是在既定的模型下不断地调超参数

这个过程肯定是要经历不断地尝试的。但是切记！！==不要使用测试集进行调优。==如果使用测试集进行调优的话，可能算法效果看起来不错，但是实际部署会效果很差。这样的方式其实就等于你把测试集当做了，训练集。通过测试集训练出来的模型使用测试集进行测试自然效果很好，但是实际上就可能过拟合。

测试数据集只使用一次，即在训练完成后评价最终的模型时使用。

为了避免这种情况，我们又设置了验证集。（其实一开始我自己看书的过程里根本分不清什么是验证集和测试集）但是在课程里讲的非常的清楚。测试集就是最后模型完成后，只使用一次进行分类器质量测试使用。超参数的调优后的测试都通过验证集来完成。

2.KNN实现

还是上面NN的那段代码，以CIFAR-10为例，我们可以用49000个图像作为训练集，用1000个图像作为验证集，下面就是划分验证集和KNN实现代码：

import numpy as np
import pickle
import os
from collections import Counter

def load_CIFAR10(path):
    Xtr, Ytr, Xte, Yte = [], [], [], []

    for i in range(1, 6):
        filename = os.path.join(path, 'data_batch_%d' % i)
        with open(filename, 'rb') as f:
            data = pickle.load(f, encoding='latin1')
            Xtr.extend(data['data'])
            Ytr.extend(data['labels'])

    with open(os.path.join(path, 'test_batch'), 'rb') as f:
        data = pickle.load(f, encoding='latin1')
        Xte.extend(data['data'])
        Yte.extend(data['labels'])
    return np.array(Xtr), np.array(Ytr), np.array(Xte), np.array(Yte)
    

class NearestNeighbor(object):
    def __init__(self):
        pass

    def train(self, X, y):
        self.Xtr = X
        self.ytr = y

    def predict(self, X, k=1):
        num_test = X.shape[0]
        Ypred = np.zeros(num_test, dtype=self.ytr.dtype)
        Ypre_k = np.zeros(k, dtype=self.ytr.dtype)

        for i in range(num_test):
            distance = np.sum(np.abs(self.Xtr - X[i, :]), axis= 1)
            min_dis = np.sort(distance)[:k] # 获取前K个最小的值的索引
            for j in range(k):
                Ypre_k[j] = self.ytr[min_index[j]] # 直接获取标签
            
            Ypred[i] = Counter(Ypre_k).most_common(1)[0][0] # 对标签进行统计并取出第一个频率最高的标签

        return Ypred   

nn = NearestNeighbor()
Xtr, ytr, Xte, yte = load_CIFAR10(r'C:\Users\Mango\Desktop\cifar-10-batches-py')
Xtr_rows = Xtr.reshape(Xtr.shape[0], 32*32*3)
Xte_rows = Xte.reshape(Xte.shape[0], 32*32*3)
Xval_row = Xtr_rows[:1000, :]
Yval = ytr[:1000]
Xtr_rows = Xtr_rows[1000:, :]
ytr = ytr[1000:]
vaildation_accuracies = []

for k in [1, 3, 5, 10, 20, 50]:
    nn.train(Xte_rows, ytr)
    Yte_predict = nn.predict(Xval_row, k = k)
    acc = np.mean(Yte_predict == ytr)
    print("accuracy: %f" % acc)
    vaildation_accuracies.append((k, acc))

最后我们会绘出分析图，来分析那个K值表现最好。然后再用该K值跑测试集，来得到该分类器真正的性能。下面还是贴出那句重要的话。

把训练集分成训练集和验证集。使用验证集来对所有超参数调优。最后只在测试集上跑一次并报告结果。

3.交叉验证

一般当数据集较小的情况下，为了能够充分的利用数据集。我们将数据集分成5份，其中4份是训练集，一份是验证集，然后循环着其中4份做训练集使用，另一份做验证集使用。最后取五次的平均作为结果。下面是交叉验证下绘制的分析图。

上图就是交叉验证5份的K值调优图。X轴代表着在调优过程中K值的变化，Y轴代表着准确率。可以看出K=7的时候性能最佳。

交叉验证一般被分割成1份、3份、10份，常用的分割模式，大概是使用数据集50%~90%。然后训练集会被均分。图上绿色的代表训练集，黄色的是验证集，红色的是测试集。如果是交叉验证那么久循环着使用训练集和验证集。

8.小结

NN在图像分类中几乎不会应用。因为NN分类器在数据维度较低的情况下效果不错，而图像往往具有较高的维度。而高维度之间的距离通常是反直觉的（意思就是跟你常识不一样）例如下图：

右边几张图片与最左边的原始图片L2距离是一样的，所以感官上的感觉往往与像素距离是不同的。这也就是为什么NN分类器比较辣鸡的原因。