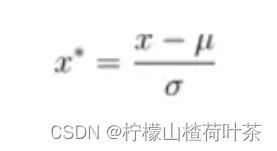cs231n assignment1——SVM
整体思路
- 加载CIFAR-10数据集并展示部分数据
- 数据图像归一化,减去均值(也可以再除以方差)
- svm_loss_naive和svm_loss_vectorized计算hinge损失,用拉格朗日法列hinge损失函数
- 利用随机梯度下降法优化SVM
- 在训练集和验证集计算准确率,保存最好的模型在测试集进行预测计算准确率
加载展示划分数据集
加载CIFAR-10数据集
# Load the raw CIFAR-10 data.
#加载CIFAR-10数据集
cifar10_dir = 'cs231n/datasets/cifar-10-batches-py'
# Cleaning up variables to prevent loading data multiple times (which may cause memory issue)
#清理变量以防止多次加载数据
try:
del X_train, y_train
del X_test, y_test
print('Clear previously loaded data.')
except:
pass
X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)
# As a sanity check, we print out the size of the training and test data.
#打印出训练和测试数据的大小。
print('Training data shape: ', X_train.shape)
print('Training labels shape: ', y_train.shape)
print('Test data shape: ', X_test.shape)
print('Test labels shape: ', y_test.shape)
# Visualize some examples from the dataset.
#可视化部分数据
# We show a few examples of training images from each class.
#从每个类别中展示一些训练图片
classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
num_classes = len(classes)
samples_per_class = 7
for y, cls in enumerate(classes):
idxs = np.flatnonzero(y_train == y)
idxs = np.random.choice(idxs, samples_per_class, replace=False)
for i, idx in enumerate(idxs):
plt_idx = i * num_classes + y + 1
plt.subplot(samples_per_class, num_classes, plt_idx)
plt.imshow(X_train[idx].astype('uint8'))
plt.axis('off')
if i == 0:
plt.title(cls)
plt.show()
划分数据集
# Split the data into train, val, and test sets. In addition we will
# create a small development set as a subset of the training data;
# we can use this for development so our code runs faster.
#将数据集划分为训练集49000张,测试集1000张和验证集1000张
#创建小样本数据加速训练
num_training = 49000
num_validation = 1000
num_test = 1000
num_dev = 500
# Our validation set will be num_validation points from the original
# training set.
#验证集取自原始训练集
mask = range(num_training, num_training + num_validation)
X_val = X_train[mask]
y_val = y_train[mask]
# Our training set will be the first num_train points from the original
# training set.
#训练集也取自原始训练集
mask = range(num_training)
X_train = X_train[mask]
y_train = y_train[mask]
# We will also make a development set, which is a small subset of
# the training set.
mask = np.random.choice(num_training, num_dev, replace=False)
X_dev = X_train[mask]
y_dev = y_train[mask]
# We use the first num_test points of the original test set as our
# test set.
mask = range(num_test)
X_test = X_test[mask]
y_test = y_test[mask]
print('Train data shape: ', X_train.shape)
print('Train labels shape: ', y_train.shape)
print('Validation data shape: ', X_val.shape)
print('Validation labels shape: ', y_val.shape)
print('Test data shape: ', X_test.shape)
print('Test labels shape: ', y_test.shape)
数据集格式转换
# Preprocessing: reshape the image data into rows
#将图像数据转化为行
X_train = np.reshape(X_train, (X_train.shape[0], -1))
X_val = np.reshape(X_val, (X_val.shape[0], -1))
X_test = np.reshape(X_test, (X_test.shape[0], -1))
X_dev = np.reshape(X_dev, (X_dev.shape[0], -1))
# As a sanity check, print out the shapes of the data
#输出数据集形状
print('Training data shape: ', X_train.shape)
print('Validation data shape: ', X_val.shape)
print('Test data shape: ', X_test.shape)
print('dev data shape: ', X_dev.shape)
图像数据归一化
# Preprocessing: subtract the mean image
#减去均值
# first: compute the image mean based on the training data
#计算训练数据的均值
mean_image = np.mean(X_train, axis=0)
print(mean_image[:10]) # 输出部分元素
plt.figure(figsize=(4,4))
plt.imshow(mean_image.reshape((32,32,3)).astype('uint8')) # visualize the mean image
plt.show()
# second: subtract the mean image from train and test data
#减去均值(更严谨的话可以继续除以方差)
X_train -= mean_image
X_val -= mean_image
X_test -= mean_image
X_dev -= mean_image
# third: append the bias dimension of ones (i.e. bias trick) so that our SVM
# only has to worry about optimizing a single weight matrix W.
#数据维度转变简便计算优化权重矩阵W
X_train = np.hstack([X_train, np.ones((X_train.shape[0], 1))])
X_val = np.hstack([X_val, np.ones((X_val.shape[0], 1))])
X_test = np.hstack([X_test, np.ones((X_test.shape[0], 1))])
X_dev = np.hstack([X_dev, np.ones((X_dev.shape[0], 1))])
print(X_train.shape, X_val.shape, X_test.shape, X_dev.shape)
评估多类 SVM 损失函数的函数
所以我们在linear_svm.py中完善svm_loss_naive
def svm_loss_naive(W, X, y, reg):
"""
Structured SVM loss function, naive implementation (with loops).
Inputs have dimension D, there are C classes, and we operate on minibatches
of N examples.
Inputs:
- W: A numpy array of shape (D, C) containing weights.
- X: A numpy array of shape (N, D) containing a minibatch of data.
- y: A numpy array of shape (N,) containing training labels; y[i] = c means
that X[i] has label c, where 0 <= c < C.
- reg: (float) regularization strength
Returns a tuple of:
- loss as single float
- gradient with respect to weights W; an array of same shape as W
"""
#梯度矩阵初始化
dW = np.zeros(W.shape) # initialize the gradient as zero
# compute the loss and the gradient
#计算损失和梯度
num_classes = W.shape[1]
num_train = X.shape[0]
loss = 0.0
for i in range(num_train):
#W*Xi
score = X[i].dot(W)
correct_score = score[y[i]]
for j in range(num_classes):
#预测正确
if j == y[i]:
continue
#W*Xi-Wyi*Xi+1
margin = score[j] - correct_score + 1 # 拉格朗日
if margin > 0:
loss += margin
# Right now the loss is a sum over all training examples, but we want it
# to be an average instead so we divide by num_train.
#平均损失
loss /= num_train
#加上正则化λ||W||²
# Add regularization to the loss.
loss += reg * np.sum(W * W)
#############################################################################
# TODO: #
# Compute the gradient of the loss function and store it dW. #
# Rather that first computing the loss and then computing the derivative, #
# it may be simpler to compute the derivative at the same time that the #
# loss is being computed. As a result you may need to modify some of the #
# code above to compute the gradient. #
#############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
dW /= num_train
dW += reg * W
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return loss, dW
评估svm_loss_naive函数
# Evaluate the naive implementation of the loss we provided for you:
from cs231n.classifiers.linear_svm import svm_loss_naive
import time
# generate a random SVM weight matrix of small numbers
# 随机初始化权重矩阵
W = np.random.randn(3073, 10) * 0.0001
#计算梯度和损失
loss, grad = svm_loss_naive(W, X_dev, y_dev, 0.000005)
print('loss: %f' % (loss, ))
在验证集计算梯度损失
数值估计损失函数的梯度,并将数值估计值与计算的梯度进行比较
# Once you've implemented the gradient, recompute it with the code below
# and gradient check it with the function we provided for you
# Compute the loss and its gradient at W.
#计算损失和梯度
loss, grad = svm_loss_naive(W, X_dev, y_dev, 0.0)
# Numerically compute the gradient along several randomly chosen dimensions, and
# compare them with your analytically computed gradient. The numbers should match
# almost exactly along all dimensions.
from cs231n.gradient_check import grad_check_sparse
f = lambda w: svm_loss_naive(w, X_dev, y_dev, 0.0)[0]
grad_numerical = grad_check_sparse(f, W, grad)
# do the gradient check once again with regularization turned on
# you didn't forget the regularization gradient did you?
loss, grad = svm_loss_naive(W, X_dev, y_dev, 5e1)
f = lambda w: svm_loss_naive(w, X_dev, y_dev, 5e1)[0]
grad_numerical = grad_check_sparse(f, W, grad)
用向量形式计算损失函数
所以我们在linear_svm.py中完善svm_loss_vectorized
def svm_loss_vectorized(W, X, y, reg):
"""
Structured SVM loss function, vectorized implementation.
Inputs and outputs are the same as svm_loss_naive.
"""
loss = 0.0
dW = np.zeros(W.shape) # initialize the gradient as zero
#############################################################################
# TODO: #
# Implement a vectorized version of the structured SVM loss, storing the #
# result in loss. #
#############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
num_train=X.shape[0]
classes_num=X.shape[1]
score = X.dot(W)
#矩阵大小变化,大小不同的矩阵不可以加减
correct_scores = score[range(num_train), list(y)].reshape(-1, 1) #[N, 1]
margin = np.maximum(0, score - correct_scores + 1)
margin[range(num_train), list(y)] = 0
#正则化
loss = np.sum(margin) / num_train
loss += 0.5 * reg * np.sum(W * W)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
#############################################################################
# TODO: #
# Implement a vectorized version of the gradient for the structured SVM #
# loss, storing the result in dW. #
# #
# Hint: Instead of computing the gradient from scratch, it may be easier #
# to reuse some of the intermediate values that you used to compute the #
# loss. #
#############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
#大于0的置1,其余为0
margin[margin>0] = 1
margin[range(num_train),list(y)] = 0
margin[range(num_train),y] -= np.sum(margin,1)
dW=X.T.dot(margin)
dW=dW/num_train
dW=dW+reg*W
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return loss, dW
然后我们对比两种损失函数计算的时间差异
# Complete the implementation of svm_loss_vectorized, and compute the gradient
# of the loss function in a vectorized way.
# The naive implementation and the vectorized implementation should match, but
# the vectorized version should still be much faster.
tic = time.time()
_, grad_naive = svm_loss_naive(W, X_dev, y_dev, 0.000005)
toc = time.time()
print('Naive loss and gradient: computed in %fs' % (toc - tic))
tic = time.time()
_, grad_vectorized = svm_loss_vectorized(W, X_dev, y_dev, 0.000005)
toc = time.time()
print('Vectorized loss and gradient: computed in %fs' % (toc - tic))
# The loss is a single number, so it is easy to compare the values computed
# by the two implementations. The gradient on the other hand is a matrix, so
# we use the Frobenius norm to compare them.
difference = np.linalg.norm(grad_naive - grad_vectorized, ord='fro')
print('difference: %f' % difference)
使用SGD优化
from __future__ import print_function
from builtins import range
from builtins import object
import numpy as np
from ..classifiers.linear_svm import *
from ..classifiers.softmax import *
from past.builtins import xrange
class LinearClassifier(object):
def __init__(self):
self.W = None
def train(
self,
X,
y,
learning_rate=1e-3,
reg=1e-5,
num_iters=100,
batch_size=200,
verbose=False,
):
"""
Train this linear classifier using stochastic gradient descent.
Inputs:
- X: A numpy array of shape (N, D) containing training data; there are N
training samples each of dimension D.
- y: A numpy array of shape (N,) containing training labels; y[i] = c
means that X[i] has label 0 <= c < C for C classes.
- learning_rate: (float) learning rate for optimization.
- reg: (float) regularization strength.
- num_iters: (integer) number of steps to take when optimizing
- batch_size: (integer) number of training examples to use at each step.
- verbose: (boolean) If true, print progress during optimization.
Outputs:
A list containing the value of the loss function at each training iteration.
"""
num_train, dim = X.shape
num_classes = (
np.max(y) + 1
) # assume y takes values 0...K-1 where K is number of classes
if self.W is None:
# lazily initialize W
self.W = 0.001 * np.random.randn(dim, num_classes)
# Run stochastic gradient descent to optimize W
loss_history = []
for it in range(num_iters):
X_batch = None
y_batch = None
#########################################################################
# TODO: #
# Sample batch_size elements from the training data and their #
# corresponding labels to use in this round of gradient descent. #
# Store the data in X_batch and their corresponding labels in #
# y_batch; after sampling X_batch should have shape (batch_size, dim) #
# and y_batch should have shape (batch_size,) #
# #
# Hint: Use np.random.choice to generate indices. Sampling with #
# replacement is faster than sampling without replacement. #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
hint=np.random.choice(num_train,batch_size,replace=True)
X_batch = X[hint]
y_batch = y[hint]
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# evaluate loss and gradient
loss, grad = self.loss(X_batch, y_batch, reg)
loss_history.append(loss)
# perform parameter update
#########################################################################
# TODO: #
# Update the weights using the gradient and the learning rate. #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
self.W = self.W - learning_rate * grad
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
if verbose and it % 100 == 0:
print("iteration %d / %d: loss %f" % (it, num_iters, loss))
return loss_history
def predict(self, X):
"""
Use the trained weights of this linear classifier to predict labels for
data points.
Inputs:
- X: A numpy array of shape (N, D) containing training data; there are N
training samples each of dimension D.
Returns:
- y_pred: Predicted labels for the data in X. y_pred is a 1-dimensional
array of length N, and each element is an integer giving the predicted
class.
"""
y_pred = np.zeros(X.shape[0])
###########################################################################
# TODO: #
# Implement this method. Store the predicted labels in y_pred. #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
scores = X.dot(self.W)
y_pred = y_pred+np.argmax(scores,1)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return y_pred
def loss(self, X_batch, y_batch, reg):
"""
Compute the loss function and its derivative.
Subclasses will override this.
Inputs:
- X_batch: A numpy array of shape (N, D) containing a minibatch of N
data points; each point has dimension D.
- y_batch: A numpy array of shape (N,) containing labels for the minibatch.
- reg: (float) regularization strength.
Returns: A tuple containing:
- loss as a single float
- gradient with respect to self.W; an array of the same shape as W
"""
pass
class LinearSVM(LinearClassifier):
""" A subclass that uses the Multiclass SVM loss function """
def loss(self, X_batch, y_batch, reg):
return svm_loss_vectorized(self.W, X_batch, y_batch, reg)
class Softmax(LinearClassifier):
""" A subclass that uses the Softmax + Cross-entropy loss function """
def loss(self, X_batch, y_batch, reg):
return softmax_loss_vectorized(self.W, X_batch, y_batch, reg)
利用SGD迭代减少损失
from cs231n.classifiers import LinearSVM
#加载SVM
svm = LinearSVM()
tic = time.time()
loss_hist = svm.train(X_train, y_train, learning_rate=1e-7, reg=2.5e4,
num_iters=1500, verbose=True)
toc = time.time()
print('That took %fs' % (toc - tic))
在训练集和验证集计算准确率
#在训练集和验证集进行预测结果,计算准确率
y_train_pred = svm.predict(X_train)
print('training accuracy: %f' % (np.mean(y_train == y_train_pred), ))
y_val_pred = svm.predict(X_val)
print('validation accuracy: %f' % (np.mean(y_val == y_val_pred), ))
计算预测数据准确率
# Use the validation set to tune hyperparameters (regularization strength and
# learning rate). You should experiment with different ranges for the learning
# rates and regularization strengths; if you are careful you should be able to
# get a classification accuracy of about 0.39 (> 0.385) on the validation set.
# Note: you may see runtime/overflow warnings during hyper-parameter search.
# This may be caused by extreme values, and is not a bug.
# results is dictionary mapping tuples of the form
# (learning_rate, regularization_strength) to tuples of the form
# (training_accuracy, validation_accuracy). The accuracy is simply the fraction
# of data points that are correctly classified.
results = {}
best_val = -1 # The highest validation accuracy that we have seen so far.
best_svm = None # The LinearSVM object that achieved the highest validation rate.
################################################################################
# TODO: #
# Write code that chooses the best hyperparameters by tuning on the validation #
# set. For each combination of hyperparameters, train a linear SVM on the #
# training set, compute its accuracy on the training and validation sets, and #
# store these numbers in the results dictionary. In addition, store the best #
# validation accuracy in best_val and the LinearSVM object that achieves this #
# accuracy in best_svm. #
# #
# Hint: You should use a small value for num_iters as you develop your #
# validation code so that the SVMs don't take much time to train; once you are #
# confident that your validation code works, you should rerun the validation #
# code with a larger value for num_iters. #
################################################################################
# Provided as a reference. You may or may not want to change these hyperparameters
#学习率
learning_rates = [1e-7, 5e-5]
#reg
regularization_strengths = [2.5e4, 5e4]
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
for learning_rate in learning_rates:
for regularization_strength in regularization_strengths:
svm = LinearSVM()
#svm训练
loss_hist = svm.train(X_train, y_train, learning_rate=learning_rate, reg=regularization_strength, num_iters=1500, verbose=True)
#在训练集预测,计算平均准确率
y_train_pred2 = svm.predict(X_train)
training_accuracy = np.mean(y_train == svm.predict(X_train))
print('training accuracy: %f' % (np.mean(y_train == y_train_pred2)))
#在验证集预测,计算平均准确率
y_val_pred2 = svm.predict(X_val)
val_accuracy = np.mean(y_val== svm.predict(X_val))
print('validation accuracy: %f' % (np.mean(y_val == y_val_pred2)))
#在训练集和验证集计算的准确率保存在results
results[(learning_rate,regularization_strength)] = (training_accuracy,val_accuracy)
print(results)
#取最大的准确率保存在best_val
if best_val < val_accuracy:
best_val = val_accuracy
best_svm = svm
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# Print out results.
for lr, reg in sorted(results):
train_accuracy, val_accuracy = results[(lr, reg)]
print('lr %e reg %e train accuracy: %f val accuracy: %f' % (
lr, reg, train_accuracy, val_accuracy))
print('best validation accuracy achieved during cross-validation: %f' % best_val)
将最好的模型保存在best_svm中,在测试集计算准确率
# Evaluate the best svm on test set
y_test_pred = best_svm.predict(X_test)
test_accuracy = np.mean(y_test == y_test_pred)
print('linear SVM on raw pixels final test set accuracy: %f' % test_accuracy)
主要解决问题:
-
损失函数和梯度的推导
-
为什么SGD越迭代可能产生loss变大的情况:
因为SGD在每一步放弃了对梯度准确性的追求,每步仅仅随机采样少量样本来计算梯度,计算速度快,内存开销小,但是由于每步接受的信息量有限,对梯度的估计出现偏差也在所难免,造成目标函数曲线收敛轨迹显得很不稳定,伴有剧烈波动,甚至有时出现不收敛的情况。(这很正常!)
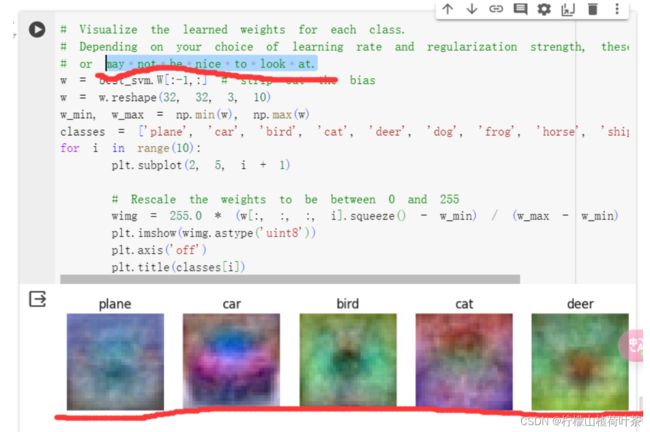
一个冷笑话(这能看出来是啥就有鬼了,果然用词很严谨
%f’ % (
lr, reg, train_accuracy, val_accuracy))
print(‘best validation accuracy achieved during cross-validation: %f’ % best_val)
将最好的模型保存在best_svm中,在测试集计算准确率
```python
# Evaluate the best svm on test set
y_test_pred = best_svm.predict(X_test)
test_accuracy = np.mean(y_test == y_test_pred)
print('linear SVM on raw pixels final test set accuracy: %f' % test_accuracy)
主要解决问题:
-
损失函数和梯度的推导
-
为什么SGD越迭代可能产生loss变大的情况:
因为SGD在每一步放弃了对梯度准确性的追求,每步仅仅随机采样少量样本来计算梯度,计算速度快,内存开销小,但是由于每步接受的信息量有限,对梯度的估计出现偏差也在所难免,造成目标函数曲线收敛轨迹显得很不稳定,伴有剧烈波动,甚至有时出现不收敛的情况。(这很正常!)
一个冷笑话(这能看出来是啥就有鬼了,果然用词很严谨