coursera 吴恩达机器学习 machine learning 作业/习题 归纳 + 脚本测试 (ex12345678)

记录一下做作业的时候遇到的问题。
coursera吴恩达机器学习网站

PS：这里代码片没写啥语言，可以查，懒得了，发现不写的话，我这里显示的是品红色（看吴恩达发现这红叫品红hhh），还是挺好看的：

用的是谷歌浏览器，然后下了个 “dark reader” 的插件，真的是完美保护狗眼，之前对着白屏真的要瞎了。
后来补充：发现只是编辑的时候是这个品红色，阅读的时候发现是白色。。

点击传送：
Ex1
Ex2
Ex3
Ex4
Ex5
Ex6
Ex7
Ex8

---

Ex1

零零碎碎的笔记：

1. nx1,或1xn的叫vector，向量，记作$R^n$，nxm的叫矩阵，记作 R ^{n x m}
2. 那个密码点了编程作业才看到的，看了视频之后想试试结果发现找不到那个密码。。。

---

1. warmUpExercise

A = eye(5);

视频也给了答案了，开门红，拿到我们第一个"Nice Work!"
注意的地方是加上分号吧，如果不用测试的话，不然一堆东西输出… 然后输出好像不影响结果，返回的东西对就可以了。

---

2. Computing Cost (for One Variable)

prediction = X*theta;
cost = (prediction - y).^2;
J = 1/(2*m)*sum(cost);

注意 .^2 加个 “.” 就是逐个元素的操作

---

3. Gradient Descent (for One Variable)

照公式写就可以了。

delta = X'*(X*theta - y); %X'可以不加括号
theta = theta - alpha/m*delta;

要注意矩阵的大小关系，比如 delta = X’ * (X * theta - y); 不能写成 (X*theta - y)*X’; 因为 X’ 是 20x2 的，一个是 20 x 1的，而delta（也就是theta的导数，大小跟theta一样）是 2x1，所以 X’ 要写在前面。这个问题手推式子的时候比较难发现。至于那些参数的长和宽是多少要用黑框打印来看看。

这个问题在第2周submitting programming assignments里面的阅读材料提到了，当时看还不知道是怎么回事。。。写完后偶然点到才发现原来在讲这个问题。

---

4. Feature Normalization
特征归一化处理，这里的normalize是 (x - 平均数) / 标准差。。。
写了个 (x - 平均数) / （max-min），一直wa。。。贴一发吧，不然白写了：

mu = mean(X_norm')
mu = mu' * ones(1,3);
sigma = std(X_norm');
X_norm = (X_norm-mu)./(max(X_norm')'*ones(1,3)-min(X_norm')'*ones(1,3))

主要是：这里的x是每行为一个例子（example），每列是一个特征（feature），所以调用mean、std、max函数的时候需要转置一下。。。因为它们应该是按一列一列计算的，在单行的vector里看不出，但是在矩阵上就看得出了。

---

5. Computing Cost (for Multiple Variables)
同 Computing Cost (for One Variable)，照贴就可以了。

---

6. Gradient Descent (for Multiple Variables)
同 Gradient Descent (for One Variable)，照贴就可以了。矩阵运算的魅力啊。

---

7. Normal Equations

theta = (pinv(X’ * X))*(X’) * y
逆矩阵的时候写了 -1 。。。不记得 X-1 代表什么了，也不是逆矩阵和转置矩阵= =

最后纪念一下 ex1 完成吧 ~

---

Ex2

1. Sigmoid Function

g = ones(size(z,1),size(z,2))./(1+exp(-z));

不容易注意的是点除（ ./ ）吧，然后注意一下分子不能写1，因为这个1是1x1维的，然后分母可以，因为 1和后面正确维度的exp(-z)相加，维度会合并到大的。

---

2. Logistic Regression Cost
哈哈，终于不得已看了一下submit文件，2和3都是调用costFunction的，不过一个检查J一个检查grad而已。然后发现3中的J写错了。其实3说得不对，J因为logistic的函数按照linear写下来的话不是凸函数，所以需要变一下形式：

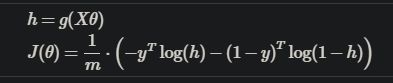
很好办，找打就是了，矩阵相乘的大小也图中处理好了：

prediction = ones(size(X*theta,1),size(X*theta,2))./(1+exp(-X*theta));
cost = (prediction - y).^2;
%J = 1/(2*m)*sum(cost); Wrong!!!
J = 1/m*(-y'*log(prediction)-(1-y)'*log(1-prediction));
grad = X'*(prediction - y)/m;

3. Logistic Regression Gradient - costFunction
想做第二个的，结果通过的是第三个（？？？）

prediction = ones(size(X*theta,1),size(X*theta,2))./(1+exp(-X*theta));
cost = (prediction - y).^2
J = 1/(2*m)*sum(cost)
grad = X'*(prediction - y)/m

因为logistic的跟linear的cost（J）和 cost 的梯度计算式子是一样的，只要把prediction（z）换一换就行了 。就前面代码复制粘贴一下。

---

4. Predict
突然发现一个文件夹（吧）里的函数可以互相调用。。

%X(1,:)
%theta
for i=1:m
  if sigmoid(X(i,:)*theta)>=0.5
    p(i) = 1;
  endif
endfor

注意的地方就是要看看X和theta的长和宽吧，要契合，i就是用来便利每行（每组）的X，然后都乘上theta就可以了，p(i)就是第i行（组）的结果。emmm，这里用了for循环，想不到怎么不用for来更新每行的p(i)。
刚写完就想到了（hh我真聪明），想起Python里面有 a = [X>0] … 差不多这种（语法好像是错的，ReLu的时候用的），大致就是把矩阵X里面每个元素判断一下，看看是否>0，然后赋给a（也是个矩阵）。然后这里在黑框里仿照了一下：

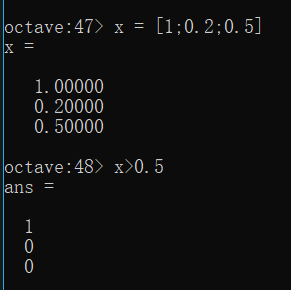
这波照葫芦画瓢很OK！所以继续仿照一下：

predict = sigmoid(X*theta)
p = predict>=0.5

就过了。不用for，直接到矩阵上运算。

---

5. &6. Regularized Logistic Regression Cost & Regularized Logistic Regression Gradient
测试的都是一个文件，合起来写了。

h = sigmoid(X*theta)
J = 1/m*(-y'*log(h)-(1-y)'*log(1-h))+lambda/2/m*(sum(theta.^2)-theta(1)*theta(1)) 
grad = X'*(h-y)/m + lambda/m*theta
grad(1) = grad(1) - lambda/m*theta(1)

J 的参照：

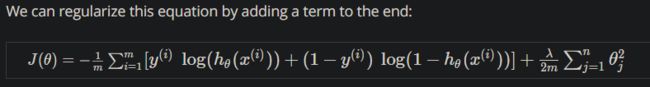
上面有说矩阵怎么算：

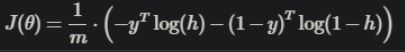
免掉了 Σ ，是因为 y是 mx1 ，yT是 1xm ，h是mx1，用 size() 打印一下就知道他们的长和宽就行了。
一开始交的是：

J = 1/m*(-y'*log(h)-(1-y)'*log(1-h))+lambda/2/m*sum(theta.^2)

就会弹出提示，说要注意θ(1)不用操作，然后改一改就行了。注意θ下标是1，而不是0，又报错了。
然后是grad的参照：网站：Regularized Linear Regression

看回昨天写的代码：

照葫芦画瓢一下：

grad = X'*(h-y)/m + lambda/m*theta
grad(1) = grad(1) - lambda/m*theta(1)

注意下标是1，然后grad(1)是不用正则化的，加上去就减掉好了。
想不出更简洁的方法，不过至少这样 J 和 grad 都不用for了，灵活运用矩阵乘法。

做完啦，最后截图纪念：

---

Ex3

1. Regularized Logistic Regression

h = sigmoid(X*theta);
J = 1/m*(-y'*log(h)-(1-y)'*log(1-h))+lambda/2/m*(sum(theta.^2)-theta(1)*theta(1)) ;
grad = X'*(h-y)/m + lambda/m*theta;
grad(1) = grad(1) - lambda/m*theta(1);

粘贴ex2的就过了… …

---

2. One-vs-All Classifier Training
卡了40分钟。。题目比较长，还有给了个fmincg不会用（该来的还是要来啊）：

initial_theta = zeros(n + 1, 1);
options = optimset('GradObj','on','MaxIter',50);
for c = 1:num_labels
  %initial_theta = zeros(n + 1, 1); 没有加上但是还是过了
  k = fmincg(@(t)(lrCostFunction(t,X,(y==c),lambda)),initial_theta,options)
  k';
  all_theta(c,:) = k';
  all_theta;
endfor

什么 iteration 就是 fmincg 跑了多少次，cost就是损失函数，脑抽了一开始还以为是报错。。。

题目思路就是跑num_labels遍，第x遍fmincg给出一个最佳的theta，放到all_theta的第x行，因为给的这个theta是个列向量，所以放到all_theta的某一行中就需要转置一下。

总结一下all_theta的第x行是用来存放第x个最佳的theta的，这个theta是针对 y 分别为1、2、3、4（因为num_labels = 4）的情况来得出的，这里x就是1~4。

为了方便转置，我用 k 来存一下列向量theta，然后转置一下 k，然后赋值给all_theta的某一行，也就是上面的代码，如果省掉一个参数 k 的话就是：

initial_theta = zeros(n + 1, 1);
options = optimset('GradObj','on','MaxIter',50);
for c = 1:num_labels
  %initial_theta = zeros(n + 1, 1); 没有加上但是还是过了
  all_theta(c,:) = fmincg(@(t)(lrCostFunction(t,X,(y==c),lambda)),initial_theta,options)'; %最后加上转置" ' "
endfor

由于没有考虑到转置的问题，一开始写的是：

for c = 1:num_labels
  all_theta(c) = fmincg(@(t)(lrCostFunction(t,X,(y==c),lambda)),all_theta(c),options)
endfor

可以说是错误百出了，首先( c )不是第c行，是矩阵按照列排下来后的第c个，然后后面 all_theta 应该是 initial_theta 。另外，细心点可以发现 initial_theta 每次遍历都没有清零，不过没有关系，因为这个 fmincg 算法足够强大，而且theta全设为0，不也不是最好的吗？

不过等等，真的需要 initial_theta 吗？all_theta 一开始不也是每一行都是 0 吗？于是我们还可以再省一个参数 initial_theta ！要做的只是把 all_theta 的行拿出来，然后稍稍转置一下，代替 initial_theta 的位置就可以了：

options = optimset('GradObj','on','MaxIter',50);
for c = 1:num_labels
  all_theta(c,:) = fmincg(@(t)(lrCostFunction(t,X,(y==c),lambda)),all_theta(c,:)',options)';
endfor

很棒，现在代码比一开始提交正确的代码要精简多了，而且也是正确的 ヾ(≧∇≦*)ヾ

---

3. One-vs-All Classifier Prediction
老方法，用 size() 输出一下 all_theta 和 X 的长和宽，知道了 X 是 m x 3 维，all_theta 是 num_labels x 3 维（4 x 3），首先 max 函数有4种：

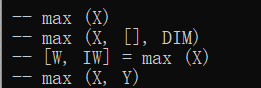
max(X) 找 X 中最大的元素
max( X , [] , 1 ) 找 X 每列最大的元素
max( X , [] , 2 ) 找 X 每行最大的元素
[ a , b ] = max (X) ，a 为 X 每列最大的元素，b 为 X 每列最大元素的下标
max( X , Y ) 为取 X 和 Y 矩阵每个位置上最大的元素

我们主要找的是 theta 乘上 X 之后，对于每一组（行），找出4种 y 谁的概率最大，得出那一种，存放在 p 对应的行中。然后用的 max 函数是得出每列的最大元素的下标，因此我们设想的是，因为有 4 种，所以搞 4 行出来，然后列就是这 4 种对应的概率，调用 max 函数的时候，就能得到每一列中，概率最大的那一种的下标。因此这个矩阵是 4 x m 大小的，所以是 all_theta * X’ 。凑出来之后得到 最大概率的下标 组成的 行向量，转置一下就是 p 了：

t = all_theta*X';
[a,b] = max(t);
p = b';

对了，不加sigmoid激活，是因为θx本来就是递增的，sigmoid也是，大的越大，所以没有必要加

---

4. Neural Network Prediction Function
写的时候有点乱，不知道最终输出的矩阵是多少，看了一眼别人代码，发现隐藏层少了加了1，输入层记得，隐藏层忘记了：

X = [ones(m, 1) X];
z2 = sigmoid(X*Theta1');
size(z2);
a2 = [ones(m,1) z2];
a3 = a2*Theta2';
t = a3';
[a,b] = max(t);
p = b';

输入层矩阵是 m x 2 -> m x 3
隐藏层输入矩阵是 m x 3 * 3 x 4 = m x 4
隐藏层输出矩阵是 m x 4 - > m x 5
输出层矩阵是 m x 5 * 5 x 4 = m x 4
最终，m x 4（或者 4 x m） 的意思是有m组输入，然后对应4组输出（的概率）
另外，过了之后看了下别人写的，原来还有[a,b] = max(A,[],2)这样的骚操作，意思差不多，不过一个针对行向量，一个针对列向量：

X = [ones(m, 1) X]
z2 = sigmoid(X*Theta1');
size(z2);
a2 = [ones(m,1) z2];
a3 = sigmoid(a2*Theta2');
[a,b] = max(a3,[],2);
p = b;

果然还是要看看别人代码，各取所长。

sigmod最后可加可不加，因为都是递增的，不过加了有 “概率” 的含义，还是加了。

磕磕绊绊吧，做完发现也不算难（万物真理：懂了就觉得不难），最后惯例截图纪念一下：

---

Ex4

Feedforward and Cost Function & Regularized Cost Function
因为复习很久没打了，生疏，卡了很久：
参考公式：

[hx,dummy] = predict(Theta1,Theta2,X);
Y = zeros(m,num_labels);
for i=1:m
  Y(i,y(i))=1;
endfor
t1 = log(hx).*Y + log(1-hx).*(1-Y);
sum_xita = sum(sum(Theta1(:,2:end).^2)) + sum(sum(Theta2(:,2:end).^2));
J = -1/m*sum(sum(t1)) + lambda/2/m*sum_xita;

% 不能够直接矩阵乘法，因为矩阵乘法的话，log(hx_k)和跟下一组y_k+1等乘在一起，是不对的
% 正确的理解应该是点乘，自己乘回自己，这里没有理解，卡了很久
% 然后theta点乘的时候，第一位是要省略不乘的，可以用语法简易截取

predict 是改了文件中的：

---

Sigmoid Gradient
根据公式：

g = sigmoid(z).*(1-sigmoid(z));

看了一下Sigmoid函数的求导证明。。有点难

---

Neural Network Gradient (Backpropagation) & Regularized Gradient
写到崩了，参考别人的
在nnCostFunction后面继续补上：

X = [ones(m,1) X];
for i=1:m
  a1 = X(i,:);  %1x3
  z2 = a1*Theta1'; %1x4
  a2 = [1 sigmoid(z2)];
  z3 = a2*Theta2';
  a3 = sigmoid(z3);
  deta3 = a3-Y(i,:); % 1 x 4
  deta3 = deta3'
  deta2 = Theta2(:,2:end)'*deta3.*sigmoidGradient(z2')
  size(z2)
  size(deta2)
  size(Theta2(:,2:end)')
  size(deta3)
  size(a2')
  Theta2_grad = Theta2_grad + deta3*a2; % 4 x 5
  Theta1_grad = Theta1_grad + deta2*a1; % 4 x 3
endfor
Theta1(:,1) = 0;
Theta2(:,1) = 0;
Theta1_grad = (Theta1_grad + lambda*Theta1)/m;
Theta2_grad = (Theta2_grad + lambda*Theta2)/m;

知识参考：



【详细过程的描述】
讲一下，写了一个下午 踩了什么坑：

1. 不清楚 a 和 z 分别是啥，搞了很久，又不看之前的笔记，刚刚贴图的时候才发现 pdf 有
2. 然后第一层输入层是要加 x0 = 1的，呵呵
3. 小写 delta（δ），那个是 ${\theta }^T\ast \delta$，我居然觉得无所谓，就写了 ${\delta }^T\ast \theta$，错到飞天
4. 最后pdf里面D应该是△和λθ都除以 m

从上午十点写到下午五点多，什么坑都踩了，纪念一下吧：

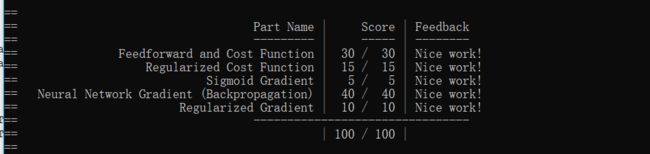
ex4 写得磕磕绊绊的，有空看看论坛的问题。

---

Ex5

Regularized Linear Regression Cost Function & Regularized Linear Regression Gradient
参考图片：

脑抽了写了注释那部分，后来看了别人的发现不用乘x的i次方，过了一会才发现x的上标指的是第几个x，而不是x的幂。

然后就是计算梯度，grad
因为这里的grad要用regression，正则化。
看回Ex2的做题笔记：（这张水印有点难去）Regularized Linear Regression

然后蓝色框住那部分就是grad，即 J 对 θ 的梯度。
然后就是完整代码：

h = zeros(m,1);
h = X*theta;
J = 1/2/m*(sum((h-y).^2))+lambda/2/m*sum(theta(2:end).^2)
grad = X'*(h-y)/m + lambda/m*theta
grad(1) = grad(1) - lambda/m*theta(1)

记得第一个θ不需要正则化。

---

Learning Curve
要求是画出随着样本数目 i 增大，求出cross vailidation 的 error 和 trainning test 的 error 。并且画出这两个的图，通常情况是：（这里 N 是 i ）

然后发现个很透的问题：我不会用Octave画图。如果不是测试的话，就会画图，但是如果submit了的话，会迭代很多次，然后画的图也有问题，画出来的图就很乱。
有点烦，网上的教程都是 matlab 的，进度有点赶，又不想学matlab，考完试暑假再看看吧。
代码：（一开始没有理解，看了别人画的图，才知道是要干嘛（随着N增加话两个 error 的图））

for i = 1:m
  theta = trainLinearReg(X(1:i,:),y(1:i,:),lambda);
  error_val(i) = linearRegCostFunction(Xval,yval,theta,0);
  %theta = trainLinearReg(X,y,lambda)
  error_train(i) = linearRegCostFunction(X(1:i,:),y(1:i,:),theta,0);
endfor

---

Polynomial Feature Mapping
计算 X，变为 [X(i) X(i).^2 X(i).^3 … X(i).^p]，代码：

for i=1:size(X,1)
  for j=1:p
  X_poly(i,j) = X(i).^j; 
endfor

看别人文章的时候，发现可以更充分运用矩阵的性质：

X 
for i=1:p
  X_poly(:,i) = X.^i; 
endfor
X_poly

突然发现打印出来，跟我理解的很不同= = ，好吧，没有认真审题，看着式子就套两个for循环，但还是做对了。
贴个看matlab图片的博客：https://blog.csdn.net/weixin_40807247/article/details/81359042
最后惯例：

PS：我觉得这次做得不是很好= = ，有点没耐心读题，不通过，想了一会就去看别人的代码，也不是说不好，但是要读好题吧。

---

Ex6

Gaussian Kernel
计算高斯kernel的公式：

||u|| 的计算方法：（u为2维）

把 u 替换成 x1 - x2，正确代码：

t = x1-x2;
sim = exp(-sum(t.^2)/(2*sigma^2))

错误代码：

sim = exp(-(x1-x2).^2/(2*sigma^2))

显然没有理解公式。

---

Parameters (C, sigma) for Dataset 3
一脸懵逼，然后想起宿友说有个文档要下载的：

Life suck. 里面有脚本，还有介绍题目的pdf，（可能还有别的数据啥的），一开始叫我们下载的东东里面有的会没有。

不过宿友说感觉没啥用就介绍一下背景，所以我一直以来没有看那个"here"的文件，所以相安无事。

这次的作业就真的顶不住了，去看了下载的文件，发现其实提示了很多，包括没有提及的函数的用法啥的，课里没讲。

题意就是找出最好的C和sigma（方差 / σ），然后用 svmPredict ，其实用 svmPredict 的时候会发现要用 svmTrain，然后里面的第四个参数要用个@啥啥的，另外svmTrain的东西也要看回代码，看代码可以发现 x1、x2 是不用定义的，因为直接赋值是（1,0），也符合课上讲的。然后 pdf 里面也提示了 C 和 sigma 推荐的参数，两重循环暴力找就行了：

vec_C = [0.01;0.03;0.1;0.3;1;3;10;30];
vec_sigma = [0.01;0.03;0.1;0.3;1;3;10;30];
%x1 = [1 2 1 5 9 8]; x2 = [0 4 -1 7 6 5]; 见有人定义了x1 x2
%x1 x2这里怎么定义没所谓，因为svmTrain中kernelFunction的用法是(1,0)
vec_errors = 10000000;
for i=1:length(vec_C)
  for j=1:length(vec_sigma)
    model= svmTrain(X, y, vec_C(i), @(x1, x2) gaussianKernel(x1, x2, vec_sigma(j)));
    pred = svmPredict(model,Xval);
    error = mean(double(pred~=yval));    
    if (error < vec_errors)
      a = i;
      b = j;
      vec_errors = error;
    endif
  endfor
endfor
C = vec_C(a); % 注意要记得赋值
sigma = vec_sigma(b);
vec_errors;
model = svmTrain(X,y,vec_C(i),@(x1, x2) gaussianKernel(x1, x2, vec_sigma(j)));
visualizeBoundaryLinear(X,y,model); % 看ex6.m知道的，可以用来看图

---

Email Preprocessing
暴力比较就行：

    for i=1:size(vocabList)
      if (strcmp(str,vocabList(i,1)))
        word_indices = [word_indices;i];
        break;
      endif
    endfor

emailFeatures
同暴力：

for i = 1:size(word_indices)
  x(word_indices(i)) = 1;
endfor

感觉这次比较简单，可能由 pdf 看吧 hh，而且实现也不用自己写：

---

Ex7

Find Closest Centroids (k-Means)
注意一下是 X 某行减掉 centroids 某行（因为centroids（μ）是 X 中的一个点（吧）），所以维度一样。
而不是 X(i) - centroids(j)

m = size(X,1);
for i=1:m
  min = 1000000000;
  for j=1:K
    t = X(i,:) - centroids(j,:);
    s = sum(t.^2);
    if (s

---

Compute Centroid Means (k-Means)
可以用矩阵来运算，知道有个find但不是很熟悉，后来就用for了，看了别人的进行下修改：

%自己写的：
##for i=1:K
##  cnt = 0;
##  for j=1:m
##    if (idx(j)==i)
##      centroids(i,:) += X(j,:);    
##      cnt++;
##    endif
##  endfor
##  centroids(i,:) /= cnt;
##endfor

%别人用了find的，进行更改：
for i=1:K
  t = find(idx==i);
  centroids(i,:) = sum(X(t,:))/length(t);
endfor

K-means 用于图像压缩
至此，跑一下脚本ex7：

感觉还不错，挺有趣的。

看到 pdf 里面有个关于图像压缩的，就是设置 K 个color（比如16色），然后跑 K-means。
首先要写个 kMeansInitCentroids，文件里面有：

% randidx存的是大小为X的行数的，然后把用X(randidx(1:K),:)分出打乱后的前K行
randidx = randperm(size(X,1)); % Randomly reorder the indices of examples
centroids = X(randidx(1:K),:); % Take the first K examples as centroids

关于 randperm 的用法测试如下。

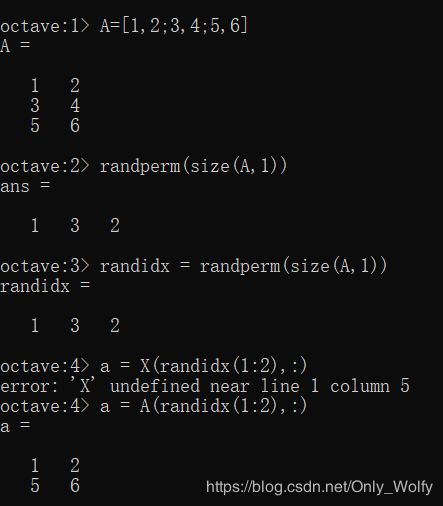
用一个变量保存一个向量，再用另一个矩阵把行关联到这个向量中，这种方法 / 过程用 C 写的话有点绕，但是这里完美运行（感觉Python这么写也行），虽然简短，但是编译器也懂你的想法，很方便。

然后命令窗口跑一下这个脚本：

K = 16时：

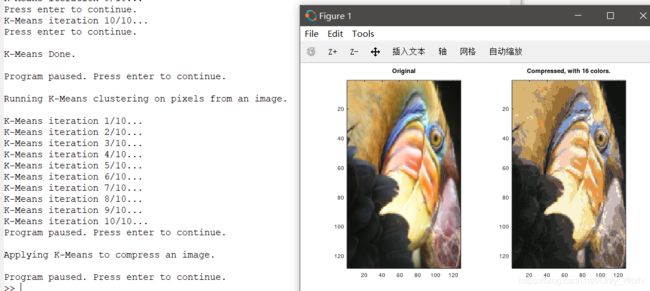
改一下脚本，K = 8：

K = 1 ：

K = 1024：

---

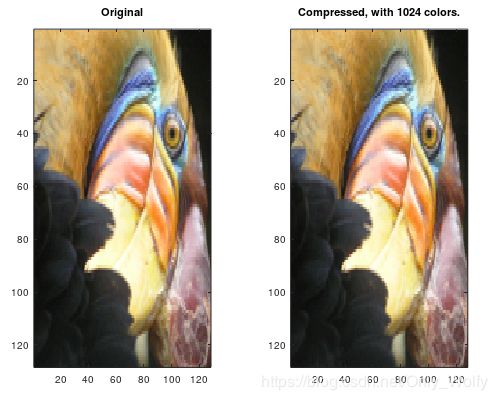
PCA

开局一张图，代码全靠编：

sigma = X'*X/m;
[U,S,X] = svd(sigma);

Project Data (PCA)

U = U(:,1:K);
Z = X*U; %懒得纸上算了，长宽瞎搞

Recover Data (PCA)

X_rec = Z*U(:,1:K)'; % 看回projectData

还有一次编程练习就结束啦！！！

---

Ex8

Estimate Gaussian Parameters

mu = mean(X)';
t = mu'.*ones(m,n);
sigma2 = sum( (X-t).^2 )'/m;

t 用来扩充一下矩阵，因为不想用 for

看了一下别人代码：

X
mu = mean(X)
size(mu)
size(X)
sigma2=sum((X - mu) .^ 2)/m;

emmm跑出来也是对的。。。
发现 - 也跟乘一样，遵循横乘竖，我对代码还是不熟悉啊 = =

---

Select Threshold
照打就是了，注意

    pval;
    yval;
    fp = sum((pval=epsilon)&(yval==1));

    prec = tp/(tp+fp);
    rec = tp/(tp+fn);

    F1 = 2*prec*rec/(prec+rec);

---

Collaborative Filtering Cost & Collaborative Filtering Gradient
没有regularized的cost和gradient：

% without regularization 
% version 1.0
J = sum(sum((X*Theta'-Y).^2.*R))/2;
for j=1:size(R,2)
  for i=1:size(R,1)
    if (R(i,j)==1)
      [i,j];
      X_grad(i,:) += (X(i,:)*Theta(j,:)'-Y(i,j))*Theta(j,:);
      Theta_grad(j,:) += (X(i,:)*Theta(j,:)'-Y(i,j))*X(i,:);
    endif
  endfor
endfor

J 的参考：


因为 Y 是 nm * nu 大小的矩阵，所以 X 和 Theta 要换一下位置，这里是 $X\ast Thet{a}^T$
然后用R来确定某个 i 行 j 列的位置是否有效，1为有效，0为无效，所以是点乘。
最后因为 J 是个数字，所以要用两个 sum 求和一个 vector。

Gradient 的参考：

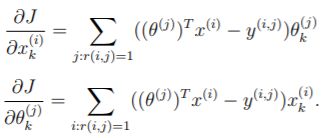
大概瞄了一眼配套 pdf 里面的提示，说要用 for 循环，然后写不出来…
最后还是去仔细思考矩阵的含义：（当然，X和X_grad含义一致（因为是梯度关系），Theta也同理）
X 矩阵：每行表示一个电影（num_movies）（下图的x1 x2），每列表示一种特征（num_features）（romance和action的程度）
Theta 矩阵：每行表示一个用户（num_users）（Alice Bob Carol Dave），每列表示一种特征（num_features）（给romance和action两个种类的喜爱程度）
配合图看更清楚一点：（注：图的Theta矩阵是一列为一个用户，每行表示一个特征，第一行0是为了和没出现X0相乘，可以忽略）

然后看回我们的定义：

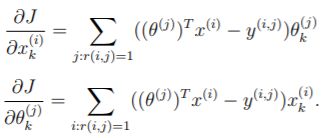
根据刚刚对矩阵的梳理和上面的公式，其实 X_grad 是每行每行地更新的，然后是（ Theta 的第 j 行的转置）和（ X 的第 i 行）相乘，注意：这里出来的是一个数字，不是矩阵。然后和 Theta 的第 j 行相乘，记得把答案累加，因为对于 i 行（第 i 个电影），有不同的分数（列 / feature），这里写的是两个循环，每次仅针对 i 行 j 列的数据，所以要把结果累加。
然后 Theta_grad 也是同理啦，这里 R（ i , j ）表示的是" if the i-th movie was rated by the j-th user "，因此对于Theta_grad 来说，更新的是 j 行，X_grad 则是 i 行。

突然发现 pdf 下一页还有提示。。。讲如何找到 j:r(i,j)=1 的：

照葫芦画瓢又有新的代码：

% without regularization 
% version 2.0
J = sum(sum((X*Theta'-Y).^2.*R))/2;
for i=1:size(R,1)
  idx = find(R(i,:)==1); % 即找出符合的 j; 
  X_grad(i,:) += (X(i,:)*Theta(idx,:)'-Y(i,idx))*Theta(idx,:);
endfor

for j=1:size(R,2)
  idx = find(R(:,j)==1); % 即找出符合的 i
  Theta_grad(j,:) += (X(idx,:)*Theta(j,:)'-Y(idx,j))'*X(idx,:);
endfor

注意最后的Theta_grad计算式子中，- Y 的结果要转置一下，不然又报错：

写完之后跑一下那个 ex8_cofi，得到一个图：

不太知道是啥…
Regularized Cost & Regularized Gradient
这里添加上 regularization，然后就只在之前的基础上稍加修改就可以了。
参考：

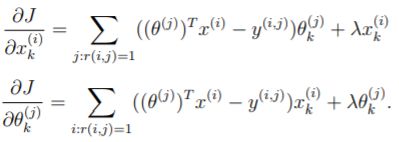
% with regularization

J = sum(sum((X*Theta'-Y).^2.*R))/2 + lambda/2*sum(sum(Theta.^2))+ lambda/2*sum(sum(X.^2));
for i=1:size(R,1)
  idx = find(R(i,:)==1); % 即找出符合的 j; 
  X_grad(i,:) += (X(i,:)*Theta(idx,:)'-Y(i,idx))*Theta(idx,:)+lambda*X(i,:);
endfor

for j=1:size(R,2)
  idx = find(R(:,j)==1); % 即找出符合的 i
  Theta_grad(j,:) += (X(idx,:)*Theta(j,:)'-Y(idx,j))'*X(idx,:)+lambda*Theta(j,:);
endfor

不过第一次的时候会超时不知道为啥。。。再submit一次就可以了：

最后跑一下ex8_cofi，感觉怪怪的，评分都是5.0，但是题目又全通过了：

最后一次编程作业啦，完结撒花！！！