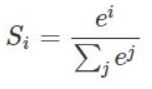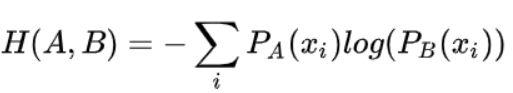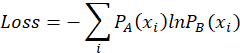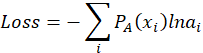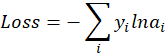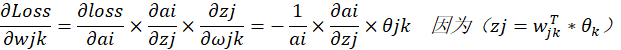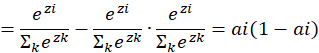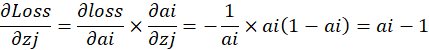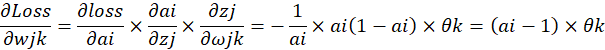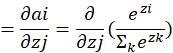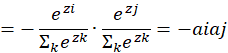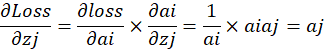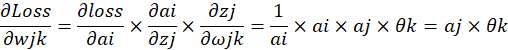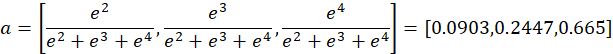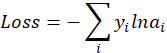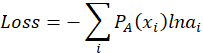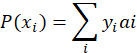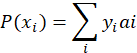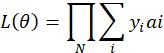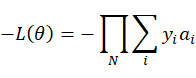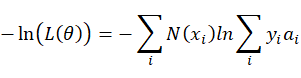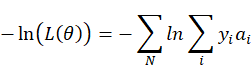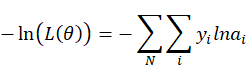Softmax激活函数 以及 多分类问题的推导

Softmax激活函数函数：

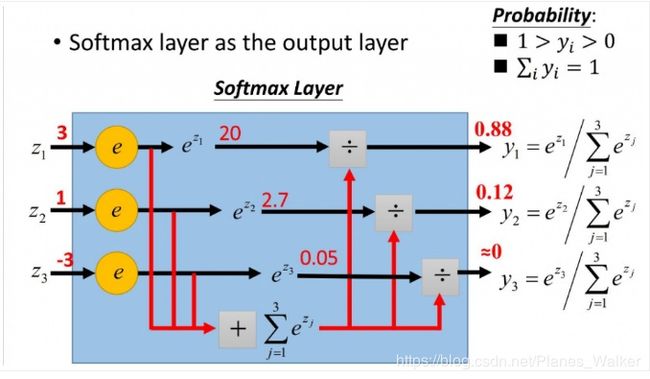
Softmax激活函数用于多分类过程中，它将多个神经元的输出，映射到（0,1）区间内，可以看成概率来理解，从而来进行多分类！

某个神经元的输出的值i ，则经过SoftMax函数的输出为Si，公式为：

示意图如下：

 

SoftMax的损失函数，以及下降方法：

要使用梯度下降，肯定需要一个损失函数，这里我们使用交叉熵作为我们的损失函数。也就是最小化训练数据与模型数据分布的KL散度 (等价于交叉熵)。

 

交叉熵的公式：

这里xi表示

所以可以建立损失函数：

其中x表示事件类型，共有i类，表示xi出现的次数,  表示事件出现的概率。

所以有：

表示事件类型的概率，就是softmax函数的输出值。

下面考虑一次实验的情况，因为一次实验只有事件发生一次，在这种情况下就是1。

设y为真实分类i时为1，其他情况为0，则对于一次实验，损失函数有：

ai是代表i类发生的概率，由SoftMax函数表示。

 

////////////////////////////////////////////////////////////////////

提一句最大似然与交叉熵的关系：更传统的机器学习说法是似然函数的最大化（当然要取log）就是交叉熵。

/////////////////////////////////////////////////////////////////////

 

让我们接着说，在现实中我们认为除了预测目标的标记为y=1，其他的分类应该都是y=0。为了形式化说明，我这里认为训练数据的真实输出为第j个为1，其它均为0，那损失函数就变成了：

并且此时yj=1，所以有了非常简单的损失函数：

 

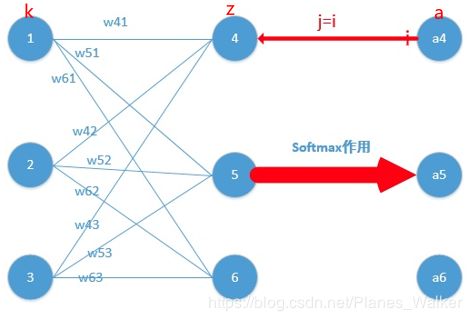
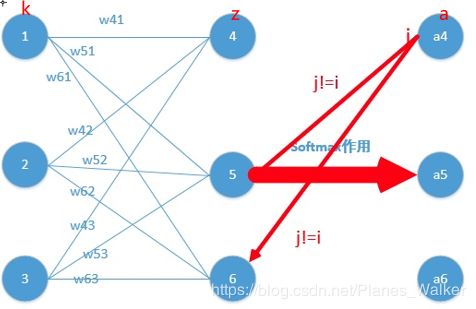
然后对某节点进行求偏导，以经典的神经网络形式来说明（也就是具有输入层、

隐藏层、输出层三个层级的神经网络，其中输入层到隐藏层是线性转换，隐藏层到输出层为softmax激活函数）拿一个语言分类器神经网络举例子：

设ai为当前经过softmax处理的输出层节点的输出，为输出层的某节点的输出（没经过softmax处理之前的输出），是隐藏层的k节点到隐藏层的权值：

由于和都已知，所以重点是求解 ：

这个式子有两种情况，第一种就是当前分类节点（所谓当前分类节点就是当前求得的经过softmax函数输出最大的节点）求导，一种是对其他分类节点求导：

(i)对当前分类节点求导， j=i时即a的下标等于z的下标的情况下：

 

:

 

带入原式，对输出层节点求偏导：

可以看到，输出层经过softmax的节点对输出层节点求偏导，当最大的softmax输出对应的分类与输出层分类一致时，求对输出层节点的偏导只要将对应的最大的softmax输出层节点输出减1即可。

进一步可以接着求，隐藏层节点到输出层节点的权值偏导：

反向传播：

 

(ii)对其他分类节点求导, i≠j时即a的下标不等于z的下标时:

 

:

 

带入原式，对输出层节点求偏导：

可以看到，输出层经过Softmax的节点对输出层节点求偏导，当最大的Softmax输出对应的分类与输出层分类不一致时，求对输出层节点的偏导只要保持不变即可。

进一步可以接着求，隐藏层节点到输出层节点的权值偏导：

反向传播：

这样所有的节点就都可以反向传播到了。

////////////////////////分割线/////////////////////////////////

举个小例子：

举个例子，通过若干层的计算，最后得到的某个训练样本的输出向量是

,那么经过softmax激活函数作用后的输出分别就是：

如果真实情况下，第二种分类是正确的，那么softmax激活函数作用后的输出对输出向量的偏导数为

然后就可以反向传播了。

////////////////////////分割线/////////////////////////////////

 

但是这还有完，因为刚刚我们解决的是一次采样的。那么多次采样形成一批的话会有什么区别呢？

我们已经知道，一次实验的损失函数是：

第一种角度：

从交叉熵角度来说：

根据前面交叉熵公式：

设发生的次数为,则有：

所以有：

相当于：

这样属于i类的实验会叠加使得系数变为，使得上面两个式子等价了，这样就可以处理批量的样本了。

 

第二种角度：

从极大似然函数来说：

一次实验中i事件发生的概率为：

一批样本中最大似然函数为：

取相反数，这样最小值就是最大值。

两边取对数

由于上式子遍历类型i，将每种事件发生的对数概率按照发生次数叠加，等同于遍历整批样本N，将每个样本发生的各事件的概率进行叠加：

然后是个常数，所以有：

 

这个式子的问题是与N有关，随着N的增加，式子有变小的趋势。所以要进行归一化，除以这批样本的总数：

这样就和上面的式子一致了。

 

 

 

参考：

https://www.zhihu.com/question/23765351/answer/240869755

Softmax 函数的特点和作用是什么？

https://www.cnblogs.com/yanshw/p/10443735.html

softmax与多分类

https://www.zhihu.com/question/65288314/answer/849294209

为什么交叉熵（cross-entropy）可以用于计算代价？