用YOLOV2对垃圾进行目标检测《二》

天下武功为快不破 ————————————————搬砖的缘由

二、使用K-means选择archor(瞄框)的形状

K-means聚类有三个步骤：
步骤1：设置集群数量并初始化集群中心
步骤2：将每个项目分配给最近的群集中心。
步骤3：将聚类中心计算为聚类中所有案例的平均值（或中位数）。
重复步骤1和2，直到两次连续迭代产生相同的聚类中心

在步骤1中，使用1-IOU计算到群集中心的距离
在步骤2中，使用中位数来计算聚类中心。

1. standardize bounding box width and hight

def stand_wh():
	wh = []
	for anno in train_image: # train_image来自上一节中最后得到的数据
	    aw = float(anno['width'])  # width of the original image
	    ah = float(anno['height']) # height of the original image
	    for obj in anno["object"]:
	        w = (obj["xmax"] - obj["xmin"])/aw # make the width range between [0,GRID_W)
	        h = (obj["ymax"] - obj["ymin"])/ah # make the width range between [0,GRID_H)
	        temp = [w,h]
	        wh.append(temp)
	wh = np.array(wh)
	print("clustering feature data is ready. shape = (N object, width and height) =  {}".format(wh.shape))

2. 计算IOU

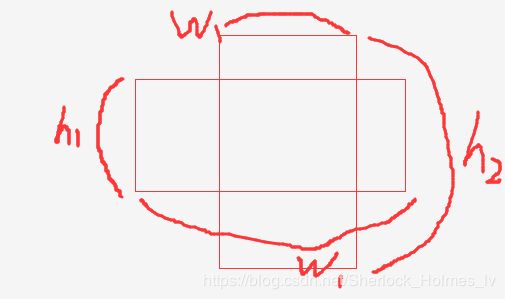
$$intersection=min(w1,w2)\ast min(h1,h2)$$

$$union=w1\ast h1+w2\ast h2$$

$$IOU=\frac{intersection}{union-intersection}$$

def iou(box, clusters):
    '''
    :param box:      np.array of shape (2,) containing w and h
    :param clusters: np.array of shape (N cluster, 2) 
    '''
    x = np.minimum(clusters[:, 0], box[0]) 
    y = np.minimum(clusters[:, 1], box[1])

    intersection = x * y
    box_area = box[0] * box[1]
    cluster_area = clusters[:, 0] * clusters[:, 1]

    iou_ = intersection / (box_area + cluster_area - intersection)

    return iou_

3. 计算kmeans

def kmeans(boxes, k, dist=np.median,seed=1):
    """
    Calculates k-means clustering with the Intersection over Union (IoU) metric.
    :param boxes: numpy array of shape (r, 2), where r is the number of rows
    :param k: number of clusters
    :param dist: distance function
    :return: clusters:集群中心点
    """
    rows = boxes.shape[0]

    distances     = np.empty((rows, k)) ## N row x N cluster
    last_clusters = np.zeros((rows,))

    np.random.seed(seed)

    # initialize the cluster centers to be k items
    clusters = boxes[np.random.choice(rows, k, replace=False)]

    while True:
        # Step 1: allocate each item to the closest cluster centers
        for icluster in range(k): 
            distances[:,icluster] = 1 - iou(clusters[icluster], boxes)

        nearest_clusters = np.argmin(distances, axis=1)

        if (last_clusters == nearest_clusters).all():
            break
            
        # Step 2: calculate the cluster centers as mean (or median) of all the cases in the clusters.
        for cluster in range(k):
            clusters[cluster] = dist(boxes[nearest_clusters == cluster], axis=0)

        last_clusters = nearest_clusters

    return clusters, nearest_clusters, distances

kmax = 11
wh = stand_wh()
dist = np.mean
results = {}
for k in range(2,kmax):
    clusters, nearest_clusters, distances = kmeans(wh,k,seed=2,dist=dist)
    WithinClusterMeanDist = np.mean(distances[np.arange(distances.shape[0]),nearest_clusters])
    result = {"clusters":             clusters,
              "nearest_clusters":     nearest_clusters,
              "distances":            distances,
              "WithinClusterMeanDist": WithinClusterMeanDist}
    print("{:2.0f} clusters: mean IoU = {:5.4f}".format(k,1-result["WithinClusterMeanDist"]))
    results[k] = result

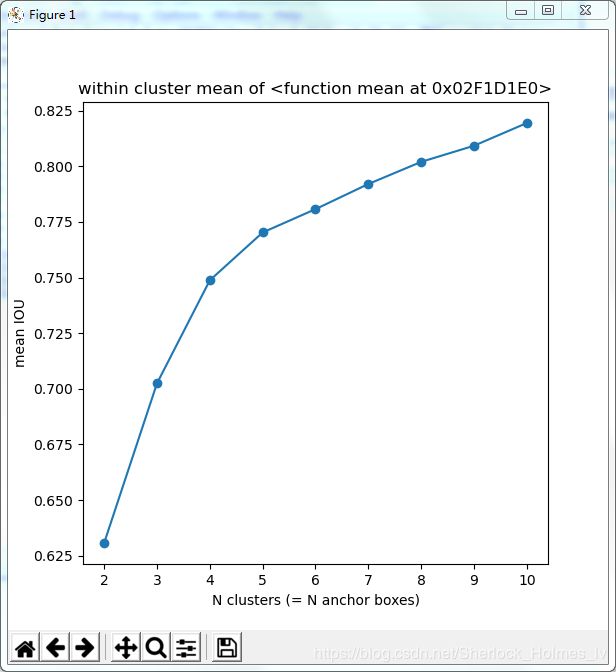
4. Elbow方法画出kmeans随着k的增加的变化

plt.figure(figsize=(6,6))
plt.plot(np.arange(2,kmax),
         [1 - results[k]["WithinClusterMeanDist"] for k in range(2,kmax)],"o-")
plt.title("within cluster mean of {}".format(dist))
plt.ylabel("mean IOU")
plt.xlabel("N clusters (= N anchor boxes)")
plt.show()

从图中很明显可以看到k=4后直线的斜率变小

[[0.39456522 0.46487029]
[0.40708786 0.84806669]
[0.82108028 0.60499731]
[0.24760711 0.32905857]]